Hard-core-Prozess
Ein Hard-core-Prozess ist ein stochastischer Punktprozess, bei dem aufeinanderfolgende Ereignisse einen festgelegten Mindestabstand zueinander einhalten. Aus Sicht der stochastischen Geometrie bestehen -dimensionale Punktfelder, die durch Hard-core-Prozesse erzeugt wurden, aus den Mittelpunkten -dimensionaler, sich nicht gegenseitig durchdringender Kugeln mit vorgegebenem Durchmesser. Siehe auch Modell harter Kugeln.

Je nach der Art und Weise, wie die Punkte erzeugt werden, lassen sich verschiedene Hard-core-Prozesse mit unterschiedlichen Eigenschaften beschreiben. Hard-core-Prozesse werden hauptsächlich in der theoretischen Ökologie und Physik der kondensierten Materie zur Modellierung verschiedener Phänomene angewandt. Weitere Anwendungen finden Hard-core-Prozesse in der Computergrafik, wo sie auch als Poisson-disk- oder Blue-noise-Abtastung bezeichnet werden.
Beispiel: Einparkproblem
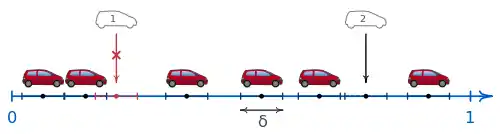
Ein einfaches Beispiel eines Hard-core-Prozesses ist das „Random car parking problem“ („Problem des zufälligen Einparkens“), das 1958 von Alfréd Rényi beschrieben wurde.[1] Auf der Strecke (der Straße) werden nacheinander zufällig Positionen gewählt. Um jede dieser Positionen wird ein Intervall der Länge (ein Auto) platziert, sofern es keines der bisher platzierten Intervalle überlappt. Dabei handelt es sich um einen eindimensionalen Hard-core-Prozess, da die Mittelpunkte der Intervalle einen Mindestabstand von einhalten.
Die rein zufällige Wahl von Positionen, ohne Einhaltung eines Mindestabstands, wird durch den Poisson-Prozess modelliert. Ein Beispiel für einen Poisson-Prozess ist das Auftreffen von Regentropfen auf dem Boden. Der Poisson-Prozess kann demnach als Hard-core-Prozess mit aufgefasst werden.
Meist sind nur vollständige Hard-core-Punktfelder von praktischem Interesse, also Punktfelder, bei denen der zur Generierung verwendete Hard-core-Prozess beendet ist und kein weiterer Punkt mehr in die vorgegebene Fläche hinzugefügt werden kann. Je nach Mindestabstand und je nachdem, wie eng ein Prozess die Punkte platziert, enthält ein vollständiges Hard-core-Punktfeld mehr oder weniger Punkte. Rényi interessierte sich für den Erwartungswert der Anzahl von Intervallen, die durch zufälliges Einparken platziert werden können.
Verschiedene Hard-core-Prozesse und ihre Simulation
Simple sequential inhibition
Das im vorherigen Abschnitt beschriebene Prozess beim Einparkproblem lässt sich auf zwei und höhere Dimensionen verallgemeinern; er wird in der Statistik im Allgemeinen als Simple sequential inhibition (SSI), in der Physik und Chemie als Random sequential adsorption (RSA), in der Sequenzplanung als On-line packing und in der Computergrafik als Dart throwing bezeichnet. Hierbei werden nach und nach Punkte von einem Poisson-Prozess erzeugt, aber nur jene berücksichtigt, die den Mindestabstand zu allen bisher beibehaltenen Punkten einhalten.
Algorithmisch lässt sich die Erzeugung von SSI-Punktfeldern mit folgendem Pseudocode beschreiben. ξ steht hierbei für eine zufällig generierte reelle Zahl zwischen 0 und 1 (oder, bei mehrdimensionalen Punktfeldern, für Tupel solcher Zufallszahlen).
Punktfeld ← (leer)
Wiederhole n mal
Kandidat ← ξ
Für jeden Existierender_Punkt in Punktfeld
Wenn ||Kandidat - Existierender_Punkt|| < δ
Nächstes n
Füge Kandidat zu Punktfeld hinzu
Erster matérnscher Prozess
Bertil Matérn beschrieb drei Arten von Hard-core-Prozessen, die durch Ausdünnung eines Poisson-Prozesses entstehen, d. h. durch das nachträgliche Löschen bestimmter Punkte, die von einem Poisson-Prozesses erzeugt wurden.[2] Anders als beim im vorherigen Abschnitt beschriebenen SSI-Prozess werden Punkte erst gelöscht, nachdem das vollständige Poisson-Punktfeld erzeugt wurde. Beim ersten matérnschen Prozess werden alle Punkte gelöscht, deren nächstgelegener Nachbarpunkt näher liegt als der Mindestabstand. Falls mehrere Punkte zu nahe beieinander liegen, so werden sie alle gelöscht.
Der Algorithmus zur Erzeugung von Punktfeldern nach dem ersten matérnschen Prozess ist wie folgt:
Punktfeld ← (leer) Wiederhole n mal Punkt ← ξ Füge Punkt zu Punktfeld hinzu Zu_löschende_Punkte ← (leer) Für jeden Punkt in Punktfeld Für jeden Nachbarpunkt in Punktfeld Wenn ||Punkt - Nachbarpunkt|| < δ Wenn Punkt nicht in Zu_löschende_Punkte vorhanden Füge Punkt zu Zu_löschende_Punkte hinzu Nächster Punkt Für jeden Punkt in Zu_löschende_Punkte Lösche Punkt aus Punktfeld
Zweiter matérnscher Prozess
Beim zweiten matérnschen Prozess werden die vom Poisson-Prozess erzeugten Punkte mit einer aufsteigenden „Markierung“ versehen. Anschließend werden alle Punkte beibehalten, die innerhalb des Mindestabstands keine vorher erzeugten Nachbarpunkte (mit einer niedrigeren Markierung) haben.
Der Algorithmus für den zweiten matérnschen Prozess lautet folgendermaßen:
Punktfeld ← (leer) Für jedes k von 1 bis n Punkt ← ξ Punkt.Markierung ← k Füge Punkt zu Punktfeld hinzu Zu_löschende_Punkte ← (leer) Für jeden Punkt in Punktfeld Für jeden Nachbarpunkt in Punktfeld Wenn ||Punkt - Nachbarpunkt|| < δ und Nachbarpunkt.Markierung < Punkt.Markierung Wenn Punkt nicht in Zu_löschende_Punkte vorhanden Füge Punkt zu Zu_löschende_Punkte hinzu Nächster Punkt Für jeden Punkt in Zu_löschende_Punkte Lösche Punkt aus Punktfeld
Dritter matérnscher Prozess
Matérn erwähnte kurz einen dritten Prozess, der wie der zweite beginnt. Anschließend wird der gleiche Prozess mit den Punkten des Poisson-Prozesses, die keine Nachbarpunkte der bisher ausgewählten Punkte sind, so lange wiederholt, bis keine neuen Punkte mehr ausgewählt werden können. Der Algorithmus lautet wie folgt:
Punktfeld ← (leer) Kandidaten ← (leer) Für jedes k von 1 bis n Punkt ← ξ Punkt.Markierung ← k Füge Punkt zu Kandidaten hinzu NeuePunkte ← Wahr Wiederhole solange NeuePunkte NeuePunkte ← Falsch Für jeden Punkt in Kandidaten Für jeden Nachbarpunkt in Kandidaten Wenn ||Punkt - Nachbarpunkt|| < δ und Nachbarpunkt.Markierung < Punkt.Markierung Nächster Punkt Füge Punkt zu Punktfeld hinzu NeuePunkte ← Wahr Zu_löschende_Punkte ← (leer) Für jeden Kandidat in Kandidaten Für jeden Punkt in Punktfeld Wenn ||Punkt - Kandidat|| < δ Wenn Punkt nicht in Zu_löschende_Punkte vorhanden Füge Punkt zu Zu_löschende_Punkte hinzu Nächster Punkt Für jeden Punkt in Zu_löschende_Punkte Lösche Punkt aus Kandidaten
Es wurde ein effizienterer Algorithmus zur Simulation von Matérn-III-Punktfeldern beschrieben.[3]
Dead leaves model
Ein weiterer Hard-core-Prozess ist das Dead leaves model („Modell der abgestorbenen Blätter“), auch Non-overlapping germ-grain model („Modell der nicht-überdeckenden Samenkörner“) genannt.[4] Bei diesem Prozess werden Kreise mit Durchmesser δ zufällig in der Ebene platziert, wobei sie vorhandene Kreise überdecken können. Das Hard-core-Punktfeld besteht aus den Mittelpunkten der nicht überdeckten Kreise (der oberen Schicht), nachdem unendlich viele Kreise hinzugefügt wurden. In endlicher Zeit simulieren lässt sich der Prozess, indem neue Kreise nicht über, sondern unter die vorhandenen Kreise platziert werden und der Vorgang abgebrochen wird, sobald die gesamte Fläche abgedeckt ist.[5] Der Prozess lässt sich auf andere Dimensionen übertragen.
Simulation von Kugelpackungen
In der Festkörperphysik wurden besondere Hard-core-Prozesse entwickelt, um dichte zufällige Kugelpackungen zu simulieren und zu untersuchen. Üblicherweise werden zur Simulation dieser Punktprozesse horizontal periodische Randbedingungen gewählt.
Sedimentationsalgorithmus
Jodrey und Torys Sedimentationsalgorithmus simuliert Kugelpackungen durch das sukzessive Fallenlassen von Kugeln in einen Container.[6] Ausgangspunkt ist eine initiale Kugelschicht („Startkombination“) am Boden des Containers. Es werden dann nach und nach Kugeln hinzugefügt, die aufgrund der Gravitation nach unten fallen und dann, ohne abzuprallen, an den existierenden Kugeln entlangrollen, bis sie an einer stabilen Position zum Liegen kommen. Als stabil gilt eine Position, wenn die Kugel mindestens drei Nachbarn (oder den Boden und zwei Nachbarn) berührt. Falls nach einer festgelegten Zeit keine stabile Position für eine Kugel gefunden werden kann, wird der Versuch mit einer neuen Kugel wiederholt. Der Prozess wiederholt sich so lange, bis der Container gefüllt ist.
Die mit dem Sedimentationsalgorithmus erreichbare Dichte ist geringer als bei natürlichen Kugelpackungen; die maximale Packungsdichte des Algorithmus beträgt ungefähr 0,58.[7] Das liegt daran, dass nicht die optimale Position für die Kugeln bestimmt wird, sondern jeweils die erste akzeptiert wird. Es ist außerdem eine Unregelmäßigkeit in der Dichteverteilung entlang der vertikalen Achse feststellbar. Wegen dieser unerwünschten Eigenschaften wird der Sedimentationsalgorithmus meist nicht mehr zur Simulation dichter Kugelpackungen verwendet.
Collective-rearrangement-Algorithmen
Bei der Gruppe der Collective-rearrangement-Algorithmen bleibt die vorgegebene Anzahl der Kugeln konstant. Im Laufe der Simulation werden viele der Kugeln verschoben. Ein bekannter Algorithmus aus dieser Gruppe ist der Force-biased-Algorithmus, der auf einer Idee von Jodrey und Torey basiert.[8] Als Ausgangspunkt wird eine Menge von zufällig verteilten, eventuell überlappenden Kugeln im Container gewählt. Nur diese Ausgangskonfiguration ist zufällig, der restliche Algorithmus arbeitet deterministisch. Die Kugeln werden voneinander weg verschoben, so als ob ein abstoßendes Kraftfeld zwischen ihnen wirken würde. Gleichzeitig wird der Radius der Kugeln mit einem Faktor kleiner als 1 multipliziert. Dieser Vorgang wiederholt sich so lange, bis die Kugeln einander nicht mehr überlappen.
Ein weiteres Beispiel für einen Collective-rearrangement-Algorithmus ist der Stillinger-Lubachevsky-Algorithmus, bei dem die Kugeln vergrößert werden und häufiger bewegt werden als beim Force-biased-Algorithmus.[9] Weiterhin gibt es sogenannte Molecular-dynamics-Methoden, bei denen sich die Größe der Kugeln nicht verändert. Stattdessen bewegen sie sich gemäß Newtons Bewegungsgesetzen, wobei sie elastisch von anderen Kugeln abprallen. Ein Beispiel für einen solchen Algorithmus ist der SPACE-Algorithmus.[10]
Collective-rearrangement-Algorithmen sind in der Lage, sehr dichte Kugelpackungen zu erzeugen.
Effiziente Methoden
Für die Computergrafik wurden eigene Methoden zur Erzeugung von Hard-core-Punktfeldern entwickelt, da hier die Ausführungsgeschwindigkeit eine große Rolle spielt.
Methode von Bridson
Bridson beschrieb einen Algorithmus mit linearer Zeitkomplexität in Abhängigkeit von der Anzahl der Punkte.[11] Im Gegensatz zu vielen anderen in der Computergrafik üblichen Algorithmen eignet sich Bridsons Algorithmus für Hard-core-Punktfelder in beliebigen Dimensionen.
Der Algorithmus beginnt mit einem zufällig gewählten Ausgangspunkt, der zu einer Liste „aktiver“ Punkte hinzugefügt wird. Es wird dann ein zufälliger Referenzpunkt aus der aktiven Liste gewählt. Anschließend werden eine maximale Anzahl von Kandidatenpunkten (typischerweise bis zu ) innerhalb des Kreisringes zwischen δ und 2δ zufällig platziert. Falls ein Kandidatenpunkt den Mindestabstand zu allen bisher beibehaltenen Punkten einhält, wird er zum Punktfeld hinzugefügt und zur aktiven Liste hinzugefügt. Falls nach Versuchen kein Kandidatenpunkt den Mindestabstand einhält, wird der Referenzpunkt aus der aktiven Liste entfernt. Dieser Vorgang wiederholt sich, bis die aktive Liste leer ist.
Die lineare Zeitkomplexität wird erreicht, indem die Fläche oder der Raum in ein regelmäßiges Gitter eingeteilt wird. Die Seitenlänge der Zellen wird hierbei nicht größer als gewählt, wobei die Anzahl der Dimensionen ist. Dadurch enthält jede Zelle maximal einen Punkt, sodass bei der Prüfung auf Einhaltung des Mindestabstands nur Nachbarzellen durchsucht werden müssen. Durch ein solches Aufteilungsschema lassen sich auch viele der vorher beschriebenen Algorithmen beschleunigen.
Der Pseudocode des Algorithmus (hier ohne Aufteilungsschema) lautet wie folgt:
Punktfeld ← (leer)
AktiveListe ← (leer)
Ausgangspunkt ← ξ
Füge Ausgangspunkt zu Punktfeld hinzu
Füge Ausgangspunkt zu AktiveListe hinzu
Wiederhole solange AktiveListe ≠ (leer)
Referenzpunkt ← [zufälliger Punkt aus AktiveListe]
PunktGefunden ← Falsch
Wiederhole k mal
Kandidat ← ZufälligerPunktInKreisring(Referenzpunkt)
Für jeden Punkt in Punktfeld
Wenn ||Punkt - Kandidat|| < δ
Nächster Kandidat
Füge Kandidat zu Punktfeld hinzu
Füge Kandidat zu AktiveListe hinzu
PunktGefunden ← Wahr
Wenn PunktGefunden = Falsch
Lösche Referenzpunkt aus AktiveListe
Methode von Dunbar und Humphreys
Dunbars und Humphreys’ Algorithmus weist ebenfalls eine lineare Zeitkomplexität auf.[12] Wie auch bei Bridsons Methode werden neue Punkte in der Umgebung der bestehenden Punkte hinzugefügt. Der für neue Punkte verfügbare Bereich wird jedoch präziser mittels einer speziellen Datenstruktur, dem „ausgekehlten Kreissektor“, repräsentiert. Dadurch kann das Hard-core-Punktfeld sehr effizient erzeugt werden.
Parkettierung
Anstatt ein Hard-core-Punktfeld für die gesamte Fläche zu generieren, können mehrere kleine Kacheln mit individuellen Punktfeldern erzeugt und anschließend zusammengesetzt werden. Es wurden mehrere solcher Methoden entwickelt, die entweder quadratische Kacheln oder Wang-Kacheln verwenden.[13] Um den Mindestabstand auch an den Rändern der Kacheln so gut wie möglich einzuhalten, können die Kacheln periodische Randbedingungen aufweisen oder bestimmte Punkte je nach Zusammensetzung der Kacheln verschoben werden.
Lloyd-Algorithmus
Der Lloyd-Algorithmus[14] kann dazu verwendet werden, um den Mindestabstand eines bestehenden (Hard-core-)Punktfeldes zu erhöhen. Der Lloyd-Algorithmus geht vom Voronoi-Diagramm des Punktfeldes aus und verschiebt die Punkte in Richtung des Flächenschwerpunktes ihrer Voronoi-Zelle. Dieser Prozess wird schrittweise wiederholt. Für zweidimensionale Punktfelder konvergiert der Lloyd-Algorithmus zu 75 bis 85 % der maximalen Packungsdichte.[15]
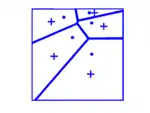
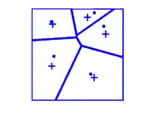
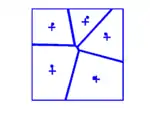
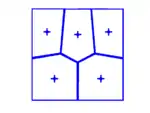
Die untenstehenden Bilder zeigen ein Punktfeld nach 1, 2, 3 und 15 Schritten des Lloyd-Algorithmus. Die Kreuze markieren die Schwerpunkte der Voronoi-Zellen.
 |
 |
 |
 |
Literatur
- A. D. Cliff, J. K. Ord: Spatial processes: models & applications, S. 103 f. Pion, London 1981, ISBN 0-85086-081-4
- Peter J. Diggle: Statistical analysis of spatial point patterns, S. 60 ff. Academic Press, London 1983, ISBN 0-12-215850-4
- Janine Illian: Statistical analysis and modelling of spatial point patterns, S. 387–397. Wiley, Chichester 2008, ISBN 978-0-470-01491-2
- Ares Lagae, Philip Dutré: A comparison of methods for generating Poisson disk distributions. Computer Graphics Forum, 27, 1 (März 2008): 114–129, ISSN 0167-7055 (PDF, 910 kB)
- Dietrich Stoyan: Simulation and characterization of random systems of hard particles. Image Analysis and Stereology 21 (Dez. 2002): 41–48, ISSN 1580-3139 (PDF, 3,7 MB)
- Dietrich Stoyan, Joseph Mecke: Stochastische Geometrie: eine Einführung, S. 87–90. Akademie-Verlag, Berlin 1983, ISSN 0084-098X
- Dietrich Stoyan, Wilfried S. Kendall, Joseph Mecke: Stochastic geometry and its applications, S. 162–166. Wiley, Chichester 1995, ISBN 0-471-95099-8
Einzelnachweise
- Alfréd Rényi: On a one-dimensional problem concerning random space-filling. A Magyar Tudományos Akadémia Matematikai Kutató Intézetének Közleményei 3 (1958): 109–127, ISSN 0541-9514
- Bertil Matérn: Spatial variation. Meddelanden från Statens Skogsförsöksanstalt 49 (1960): 1–144, ISSN 0369-2167. Siehe auch Bertil Matérn: Spatial variation (=Lecture Notes in Statistics 36), S. 47 ff. Springer, Berlin 1986, ISBN 3-540-96365-0
- Jesper Møller, Mark L. Huber, Robert L. Wolpert: Perfect simulation and moment properties for the Matérn type III process. Stochastic Processes and their Applications 120, 11 (Nov. 2010): 2142–2158, ISSN 0304-4149 (PDF, 320 kB)
- Georges Matheron: Schéma booléen séquentiel de partition aléatoire. Note géostatistique N° 89, Centre de Morphologie Mathématique, École des Mines de Paris, Fontainebleau 1968 (PDF, 550 kB)
- Wilfrid S. Kendall, Elke Thönnes: Perfect simulation in stochastic geometry. Pattern Recognition 32 (1999): 1569–1586, ISSN 0031-3203 (ps.gz, 420 kB)
- W. Steven Jodrey, Elmer M. Tory: Simulation of random packing of spheres. Simulation 32, 1 (Jan. 1979): 1–12, ISSN 0037-5497
- William M. Visscher, M. Bolsterli: Random Packing of Equal and Unequal Spheres in Two and Three Dimensions. Nature 239 (27. Okt. 1972): 504–507, ISSN 0028-0836. Zitiert in Antje Elsner: Computergestützte Simulation und Analyse zufälliger dichter Kugelpackungen, S. 21. Dissertation, Technische Universität Bergakademie Freiberg 2009 (PDF, 6,6 MB)
- W. S. Jodrey, E. M. Tory: Computer simulation of close random packing of equal spheres. Physical Review A 32 (1985): 2347–2351, ISSN 1050-2947
- Boris D. Lubachevsky, Frank H. Stillinger: Geometric properties of random disk packings. Journal of Statistical Physics 60, 5/6 (1990): 561–583, ISSN 0022-4715 (PDF, 1,5 MB)
- Piet Stroeven, Martijn Stroeven: Reconstructions by SPACE of the interfacial transition zone. Cement and Concrete Composites 23, 8 (2001): 189–200, ISSN 0958-9465
- Robert Bridson: Fast Poisson disk sampling in arbitrary dimensions. In ACM SIGGRAPH 2007 Sketches, Article 22. ACM, New York, 2007 (PDF, 110 kB)
- Daniel Dunbar, Greg Humphreys: A spatial data structure for fast Poisson-disk sample generation. In Proceedings of ACM SIGGRAPH 2006, S. 503–508. ACM, New York 2006, ISBN 1-59593-364-6 (Online)
- Siehe Lagae/Dutré für einen Vergleich
- Stuart P. Lloyd: Least squares quantization in PCM. IEEE Transactions on Information Theory 28, 2 (März 1982): 129–137, ISSN 0018-9448 (PDF, 1,2 MB)
- Lagae/Dutré, S. 6