Wang-Parkettierung
Wang-Kacheln (oder Wang Domino), entworfen 1961 von Hao Wang, sind Gruppen von Rechtecken gleicher Größe, deren Kanten je mit einer bestimmten Farbe markiert sind. Eine solche Gruppe von Kacheln stellt eine Instanz eines unentscheidbaren Entscheidungsproblems dar. Das folgende Bild zeigt einen Satz von 13 Wang-Kacheln:
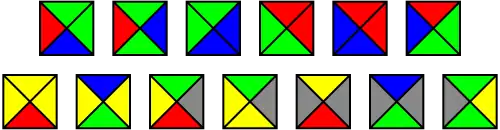
Die zu lösende Aufgabe bzw. das Entscheidungsproblem besteht darin, zu entscheiden, ob es mit einem gegebenen endlichen Satz an Kacheln möglich ist, die Ebene zu parkettieren. Dies heißt, mit beliebig vielen Kopien der Kacheln aus dem Satz die unbegrenzte Ebene lückenlos so zu füllen, dass dabei alle verwendeten Kacheln jeweils mit Seiten gleicher Farbe aneinanderstoßen. Die Kacheln dürfen dabei nicht verdreht oder gespiegelt werden.
Wang schlug 1961 einen Algorithmus vor, der dieses Problem lösen sollte. Im Beweis der Korrektheit seines Verfahrens nahm er an, dass jeder Satz von Kacheln, die die Ebene füllen, diese dabei periodisch parkettieren würde.

1966 zeigt Robert Berger jedoch, dass Wangs Vermutung falsch war. Er gab dazu einen Satz Wang-Kacheln an, mit dem man die Fläche nur aperiodisch kacheln konnte. Mit diesen Kacheln kann man zwar die Ebene lückenlos füllen, jedoch nicht so, dass dabei die Fläche von einem sich periodisch immer wiederholenden endlichen Ausschnitt gefüllt wird. Dies ist ähnlich der Lage bei der Penrose-Parkettierung oder der Anordnung der Atome in Quasi-Kristallen. Obwohl Berger ursprünglich einen Satz von 20.426 Kacheln verwendete, vermutete er, dass eine geringere Anzahl von Kacheln mit dieser Eigenschaft ebenfalls möglich wäre. In den folgenden Jahren wurden immer kleinere Sätze von Kacheln gefunden. Beispielsweise ist die oben abgebildete Gruppe aus 13 Kacheln ein von Karel Culik publizierter aperiodischer Satz.
Wangs Algorithmus zur Entscheidung, ob ein gegebener Satz von Kacheln die Ebene parkettiert, war also nicht korrekt. In der Tat existiert ein solcher Algorithmus nicht. Es ist möglich, jede Turingmaschine derart in einen Satz von Wang-Kacheln zu übersetzen, dass diese Kacheln die Ebene genau dann parkettieren, wenn die Turingmaschine nicht hält. Da das Halteproblem nicht entscheidbar ist, ist auch das Kachelungsproblem von Wang nicht entscheidbar. Umgekehrt ist das Problem semi-entscheidbar, ob eine Parkettierung nicht möglich ist. Ein entsprechender Algorithmus geht alle endlichen Teilmengen der Ebene durch und braucht nur zu erkennen, dass für eine solche eine Parkettierung nicht möglich ist. Zusammengefasst lassen sich über die Nichtparkettierbarkeit mit einem Satz von Kacheln dieselben Probleme lösen wie mit einer Turingmaschine. Präzise: Das Problem ist bezüglich der Many-one-Reduktion ein vollständiges semi-entscheidbares Problem.
Der Umstand, dass Wangs Verfahren prinzipiell nicht auf beliebige Kachelsätze anwendbar ist, macht dieses jedoch nicht nutzlos für praktische Anwendungen. Mit einer optimierten Version der ursprünglichen Methode konnte Sergio Demian Lerner zeigen, dass es keine aperiodischen Kachelsätze mit sieben oder weniger Kacheln gibt. Diese untere Grenze lässt nur noch eine schmale Lücke zur Verbesserung.
Wang-Kacheln können in verschiedenster Weise verallgemeinert werden, die alle unentscheidbar in obigem Sinne sind. Zum Beispiel sind Wang-Würfel gleich große Würfel mit gefärbten Flächen. Culik und Kari haben aperiodische Sätze von Wang-Würfeln aufweisen können.
Wangs Kacheln eignen sich wegen ihrer Einfachheit zur Herstellung einfachster Maschinen oder Modelle, die dieselbe Leistungskraft wie Turingmaschinen haben. Winfree et al. haben die Herstellbarkeit von molekularen „Kacheln“ aus Desoxyribonukleinsäure (DNA) nachgewiesen, die man als Wang-Kacheln verwenden kann. Mittal et al. haben das Gleiche auch für PNA (Peptid-Nukleinsäure) gezeigt, einer chemischen Variante der DNA.
Siehe auch
Literatur
- Hao Wang: Proving theorems by pattern recognition. Part II. In: Bell System Technical Journal. 40 (1961), S. 1–42. (Wang stellt seine Kacheln vor und vermutet, dass es keine aperiodische Kachelung gibt).
- Hao Wang: Games, logic and computers. In: Scientific American. November 1965, S. 98–106. (Stellt sie einer breiteren Öffentlichkeit vor)
- Robert Berger: The undecidability of the domino problem. Memoirs of the American Mathematical Society Number 66. AMS Bookstore, Providence (RI) 1966, ISBN 0-8218-1266-1. (Prägt den Ausdruck „Wang-Kacheln“ (Wang tiles), und stellt den ersten aperiodischen Kachelsatz vor).
- Karel Culik II: An aperiodic set of 13 Wang tiles. In: Discrete Applied Mathematics. 160, 245–251. (Zeigt einen aperiodischen Satz aus 13 Kacheln mit 5 Farben).
- Karel Culik II & Jarkko Kari: An aperiodic set of Wang cubes. In: Journal of Universal Computer Science. 1 (1995), S. 675–686. (PDF; 193 KB)
- Erik Winfree, Furong Liu, Lisa A. Wenzler & Nadrian C. Seeman: Design and Self-Assembly of Two-Dimensional DNA Crystals. In: Nature. 394 (1998), 539–544. (PDF; 734 KB)
- Philip S. Lukeman, Nadrian C. Seeman & Alexander C. Mittal: Hybrid PNA/DNA Nanosystems. In: First International Conference on Nanoscale/Molecular Mechanics (N-M2-I). Outrigger Wailea Resort, Maui (Hawaii), 2002
Weblinks
- Steven Dutchs Seite enthält viele Bilder aperiodischer Kachelung
- Englischsprachiges Paper u. a. zur Übersetzung einer Turingmaschine in einen Wang-Kachelsatz (Memento vom 19. April 2009 im Internet Archive) (PDF-Datei; 216 kB)