Gutenberg-Produktionsfunktion

Die Gutenberg-Produktionsfunktion (auch: Produktionsfunktion Typ B oder Theorie der Anpassungsformen) ist eine von Erich Gutenberg entwickelte[1] Produktionsfunktion. Sie ging aus der ertragsgesetzlichen Produktionsfunktion hervor, die auch als Produktionsfunktion Typ A bekannt ist und aus der Volkswirtschaftslehre in die Betriebswirtschaftslehre übernommen wurde. Die Gutenberg-Produktionsfunktion wird zusammen mit der Aktivitätsanalyse zu den zwei bedeutendsten Neuerungen der Produktions- und Kostentheorie in der zweiten Hälfte des 20. Jahrhunderts gezählt.[2]

Der U-förmige Verlauf des Produktionskoeffizienten a in Abhängigkeit von der Intensität d gilt als typisch für die Gutenberg-Produktionsfunktion

Die Gutenberg-Produktionsfunktion ist wie alle anderen Produktionsfunktionen ein theoretisches Modell, das Zusammenhänge zwischen den bei der Produktion verbrauchten Rohstoffmengen und den dabei erzeugten Produktionsmengen betrachtet. Sie ist die erste Produktionsfunktion, die auf die besonderen Erfordernisse der Betriebswirtschaft ausgerichtet ist[3] und bildet die Grundlage vieler weiterer Produktionsfunktionen (Typen C, D, E und F). Während frühere Produktionsfunktionen für eine gegebene Menge von Produktionsfaktoren r (Arbeitskräfte, Maschinen etc.) die maximal mögliche Produktionsmenge x angeben, ergibt sich bei Gutenberg sowohl die Produktionsmenge als auch der Faktorverbrauch aus der Anzahl n der aktiven Maschinen, der Geschwindigkeit d, mit der sie arbeiten (Intensität), und der Zeit t, während der sie aktiv sind.

Geschichte

Anfänge in der Volkswirtschaftslehre

Die Produktionstheorie entstand im 18. Jahrhundert als Teilgebiet der Preistheorie, welche selbst Teil der Volkswirtschaftslehre ist und somit noch vor der Entwicklung der Betriebswirtschaftslehre um 1900. Mithilfe der Produktionsfunktionen, die für eine gegebene Menge der Produktionsfaktoren Arbeit und Kapital die maximal mögliche Menge an Produkten angibt, wird versucht, die Angebotskurve der Unternehmen herzuleiten. Sie gibt an, wie viel die Unternehmen bei einem gegebenen Preis anbieten. Zusammen mit der Nachfragekurve der Haushalte lässt sich dann ein Marktgleichgewicht bestimmen. Die in der Volkswirtschaftslehre gebräuchlichen Produktionsfunktionen gingen davon aus, dass sich eine bestimmte Produktionsmenge durch verschiedene Kombinationen von Arbeit und Kapital erreichen lässt, was der Beobachtung entstammt, dass im Laufe der industriellen Revolution menschliche Arbeit durch Maschinen – die zum Realkapital zählen – ersetzt wurden. Die Eigenschaft, dass die Produktionsfaktoren austauschbar sind, wird als Substitutionalität bezeichnet. Außerdem hatten die frühen Produktionsfunktionen die Eigenschaft, dass sich auch bei Konstanz eines Faktors die Produktionsmenge erhöhen lässt, wenn man den Einsatz des anderen Faktors erhöht.[4] Ausgehend von der Produktionsfunktion wurde der Verbrauch der Faktoren mit den jeweiligen Beschaffungspreisen bewertet, um so zu den Kostenfunktionen zu gelangen. Mit ihnen war es dann möglich für gegebene Marktpreise der Produkte die von den Unternehmen angebotene Menge herzuleiten.

Die ertragsgesetzliche Produktionsfunktion, die Ende des 18. Jahrhunderts aufgrund von Beobachtungen in der Landwirtschaft entwickelt wurde, war die erste konkrete Produktionsfunktion. Aufgrund von Analogieschlüssen herrschte die Meinung vor, dass sie auch für die industrielle Produktion gültig sei. Sie wurde im 19. Jahrhundert zur Cobb-Douglas-Funktion weiterentwickelt. Bei beiden handelt es sich um substitutionale Produktionsfunktionen. Die gesamte Produktionstheorie wurde in die um 1900 herum entstandene Betriebswirtschaftslehre integriert. Von Interesse war hier vor allem innerhalb der Industriebetriebslehre der Zusammenhang zwischen der Produktion und den durch sie verursachten Kosten.

Gutenbergs Kritik am Stand der Produktionstheorie

Gutenberg waren durch sein Studium der Volkswirtschaftslehre diese Theorien bekannt. Nach Abschluss des Studiums arbeitete er für einige Jahre in einem Industrieunternehmen, studierte anschließend Betriebswirtschaft und wurde schließlich Professor für Betriebswirtschaft. In der zweiten Auflage von 1955 seines Hauptwerks „Die Produktion“ kritisierte er die bisherige Theorie im Allgemeinen und vor allem das Ertragsgesetz im Besonderen als für die industrielle Praxis ungeeignet, obwohl er sie in der ersten Auflage von 1951 noch verteidigte.[5] So gehe die klassische Theorie unausgesprochen von beliebiger Teilbarkeit der Faktoren Arbeit und Kapital aus. Arbeitskräfte und Maschinen seien jedoch nicht beliebig teilbar. Kritisiert wurde ebenfalls die Substitutionalität: Sie sei in der betrieblichen Realität nicht erfüllt. Stattdessen herrschen sogenannte limitationale Bedingungen vor bei denen nur eine bestimmte Kombination der Faktoren zur gewünschten Produktionsmenge führt. Für einen bestimmten Maschinentyp wird beispielsweise eine bestimmte Anzahl an Bedienern benötigt. Mehr Personal bei einer einzelnen Maschine kann nicht die Produktionsmenge erhöhen. Die Maschinenanzahl limitiert dann die maximal mögliche Produktionsmenge. Überhaupt abstrahiere die bisherige Theorie davon, wie die Faktoren in Produkte transformiert werden[6] und führe deshalb dazu, dass sie sich wenig bewährt habe.

Die neue Produktionsfunktion

Gutenberg entwickelte eine neue Produktionsfunktion, die er „Produktionsfunktion vom Typ B“ nannte, als Gegenstück zum Ertragsgesetz, das er „Produktionsfunktion vom Typ A“ nannte, das seither unter diesem Namen in der Betriebswirtschaft bekannt ist. Er teilte die Produktionsfaktoren zunächst neu ein, in menschliche Arbeit, Maschinen und Werkstoffe und stellte die Maschinen ins Zentrum seiner Betrachtung. Den Bestand an Maschinen sah er als konstant an; die Produktionsmenge jedoch als variabel über die Anzahl der eingesetzten Maschinen (quantitative Anpassung), der Intensität, mit der sie arbeiten (in produzierten Stück pro Zeit, intensitätsmäßige Anpassung) und durch ihre Einsatzdauer (zeitliche Anpassung). Er ging davon aus, dass eine Verdopplung der Maschinenzahl (bei konstanter Intensität und Einsatzdauer) auch zu einer Verdopplung des Verbrauchs an Werkstoffen führt. Gleiches gilt für eine Änderung der Einsatzdauer. Bei einer Änderung der Intensität jedoch kann keine allgemeine Aussage über den Verbrauch der anderen Faktoren gemacht werden. Diese sind für jede Maschine und jeden Faktor getrennt im Einzelfall zu ermitteln. An vielen Maschinen folgt der Verbrauch der Betriebsstoffe (Treibstoff, Schmieröl) pro hergestelltem Produkt einem u-förmigen Verlauf mit einer verbrauchsminimalen Intensität. Dieser Fall wurde von Gutenberg eingehend untersucht: Er ermittelte für jede mögliche Produktionsmenge diejenige Kombination von Maschinenanzahl, Einsatzdauer und Intensität, die zu den geringsten Kosten führt.

Rezeption

Gutenbergs Arbeiten stießen auf große Zustimmung. Seine Theorien bestimmten für etwa ein Jahrzehnt die Forschungsrichtung der Betriebswirtschaft. Das von ihm begründete Wissenschaftsprogramm wird als faktortheoretischer Ansatz bezeichnet. Die von ihm vorgeschlagene Einteilung der Produktionsfaktoren wurde verfeinert und erweitert, aber im grundsätzlichen Aufbau beibehalten. Auch zu seiner Produktionsfunktion gab es viele Arbeiten, die die Theorie ergänzten und bestätigten. Edmund Heinen entwickelte sie weiter zu der nach ihm benannten Heinen-Produktionsfunktion. Er war jedoch mit dem Stand der Theorie nicht zufrieden: „Betriebswirtschaften sind nicht ‚Veranstaltungen‘ irgendwelcher abstrakter Produktionsfaktoren, sondern Sozialsysteme, in denen Menschen […] zusammenarbeiten.“[7] Das durch ihn angestoßene Wissenschaftsprogramm bestimmte im folgenden Jahrzehnt die betriebswirtschaftliche Forschung und wird als entscheidungsorientierter Ansatz bezeichnet. Die Gutenberg-Produktionsfunktion hat sich bis heute zusammen mit dem Ertragsgesetz einen festen Platz in betriebswirtschaftlichen Lehrbüchern erhalten. Während letztere allerdings eher aus didaktischen Gründen aufgeführt wird, wird ersterer eine hohe Praxistauglichkeit bescheinigt.

Die z-Situation

Die technischen Parameter der einzelnen Maschinen werden zur sogenannten z-Situation zusammengefasst, die dann als konstant angesehen wird. Zu ihr gehören alle Werte, die für die Produktion relevant sind, sich jedoch kurzfristig nicht ändern lassen. Ein Motor lässt sich beispielsweise charakterisieren durch die Anzahl seiner Ventile (z₁), den Hubraum (z₂), der benötigten Treibstoffart (z₃), der Betriebstemperatur (z₄) und weiteren Merkmalen die durch die Konstruktion bedingt sind. Lassen sich Maschinen umrüsten (zum Beispiel lassen sich Stanzmaschinen mit verschieden geformten Werkzeugen bestücken) so bedeutet dies einen Übergang zu einer anderen z-Situation. Ebenso gehört der Bestand an Maschinen dazu; die Beschaffung neuer oder der Verkauf vorhandener Maschinen wird also als Änderung der z-Situation gewertet.[8] Von allen technischen Werten wird die Intensität $d$ besonders hervorgehoben. Sie gibt die von einer Maschine erbrachten ökonomischen Arbeitseinheiten pro Zeit an, z. B. Stück pro Stunde (bei Stückgütern) oder Meter pro Minute (bei Fließgütern).

Die Verbrauchsfunktion

Frühere Produktionsfunktionen stellten einen unmittelbaren Zusammenhang her zwischen der Produktionsmenge $x$ (auch: Ausbringungsmenge oder Output) und der Menge der verbrauchten Faktoren $r$ (meistens Rohstoffe, auch als Einsatzmenge, oder Input bezeichnet). Diese Funktionen hatten die Form $x=f(r)$ für einen einzelnen Faktor oder $x=f(r_{1},r_{2},\cdots ,r_{n})$ für $n$ verschiedene Faktoren. Bei der Gutenberg-Produktionsfunktion hängt sowohl die Produktionsmenge als auch der Faktorverbrauch von der Intensität der Produktion $d$ , der Dauer der Produktion $t$ und der Anzahl der aktiven Maschinen $m$ ab.[9]

x=d\cdot t\cdot m

{\begin{aligned}r&=a\cdot x\\&=a\cdot d\cdot t\cdot m\end{aligned}}

Dabei ist $a$ der sogenannte Produktionskoeffizient, der im Allgemeinen nicht konstant ist, sondern von der Intensität abhängt, also $a(d)$ . Wobei bei dieser Darstellungsform unterstellt wurde, dass alle Maschinen identisch sind und mit derselben Intensität und Dauer betrieben werden.

Wenn man verschiedene Intensitäten und Einsatzdauern berücksichtigen möchte, muss man für die gesamte Produktionsmenge die Produktionsmengen der einzelnen Maschinen addieren und für den gesamten Faktorverbrauch entsprechend den Verbrauch der einzelnen Maschinen:

x=d_{1}\cdot t_{1}+d_{2}\cdot t_{2}+\dotsb +d_{m}\cdot t_{m}

r=a_{1}\cdot x_{1}+a_{2}\cdot x_{2}+\dotsb +a_{m}\cdot x_{m}

In der Regel werden für die Produktion mehrere Faktoren gleichzeitig benötigt (z. B. Werkzeuge, Treibstoffe, Rohstoffe, Schmierstoffe etc.). Daher ist für alle $n$ Faktoren eine eigene Verbrauchsfunktion zu ermitteln.

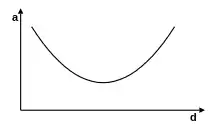
Der Produktionskoeffizient $\textstyle a(d)={\frac {r}{x}}$ kann als durchschnittlicher Verbrauch interpretiert werden (Verbrauch pro produzierten Stück). Für viele Faktorarten ergibt sich ein u-förmiger Verlauf mit einem minimalen Durchschnittsverbrauch bei der Intensität $d_{\mathrm {opt} }$ . Die zugehörigen Verbrauchsfunktionen $r$ haben dann einen s-förmigen Verlauf. Dieser Fall wurde von Gutenberg eingehend untersucht.

Kostenfunktionen reiner Anpassungen

Bei konstantem Verlauf der Stückkosten (blau), ergibt sich eine linear steigende Gesamtkostenfunktion (rot)

Kostenfunktionen stellen einen Zusammenhang her zwischen der Produktionsmenge $x$ und den durch die Produktion entstehenden Kosten. Die gesamten Kosten $K$ einer einzelnen Maschine ergeben sich, indem man den Verbrauch der Faktoren mit den jeweiligen Beschaffungspreisen $p$ multipliziert und die Kosten der einzelnen Faktoren dann addiert:[10]

{\begin{aligned}K&=r_{1}p_{1}+r_{2}p_{2}+\cdots +r_{n}p_{n}\\&=a_{1}(d)x_{1}p_{1}+a_{2}(d)x_{2}p_{2}+\cdots +a_{n}(d)x_{n}p_{n}\end{aligned}}

Teilt man die gesamten Kosten durch die Produktionsmenge, erhält man die Stückkosten $k$ :

k=K/x=a_{1}(d)p_{1}+a_{2}(d)p_{2}+\cdots +a_{n}(d)p_{n}

Fixe Kosten, die unabhängig davon entstehen ob oder wie viel produziert wird, werden üblicherweise vernachlässigt, da die Produktion keinen Einfluss darauf hat. Streng genommen handelt es sich also um die variablen Kosten $K_{v}$ und die variablen Stückkosten $k_{v}$ .

Rein intensitätsmäßige Anpassung

Konstante Gesamtkosten und fallende Stückkosten

Linear steigende Stückkosten und überlinear-steigende Gesamtkosten

u-förmiger Verlauf der Stückkosten und s-förmiger Verlauf der Gesamtkosten

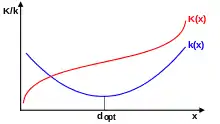
Bei der rein intensitätsmäßigen Anpassung werden die Anzahl der Maschinen und die Einsatzdauer konstant gehalten und nur die Intensität der Maschinen zwischen der minimal möglichen Intensität $d_{\mathrm {min} }$ und der maximal möglichen Intensität $d_{\mathrm {max} }$ verändert. Sie sind häufig technisch vorgegeben: Viele Motoren beispielsweise funktionieren nur innerhalb eines bestimmten Drehzahlbereiches. Die minimale Intensität kann aber durchaus Null betragen. Im Folgenden wird vereinfachend davon ausgegangen, dass mit einer einzelnen Maschine produziert wird. Der Verlauf der Kostenfunktionen ist abhängig vom Verlauf der Produktionskoeffizienten $a(d)$ .

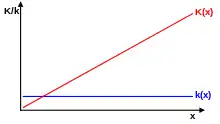
Bei Produktionskoeffizienten, die konstant sind, also unabhängig von der Intensität, ergibt sich ein waagrechter Verlauf der Stückkosten und ein linear steigender Verlauf der Gesamtkosten. Dieser Spezialfall wurde bereits vor Gutenberg durch Wassily Leontief in der nach ihm benannten Leontief-Produktionsfunktion untersucht. Ein solcher Verlauf ergibt sich oft für die Materialien, aus denen das Endprodukt besteht. Der Produktionskoeffizient ergibt sich oft direkt aus Stücklisten, Rezepten, chemischen Reaktionsgleichungen und ähnlichem. Für die Herstellung eines Fahrrades benötigt man beispielsweise genau zwei Reifen, unabhängig davon, wie schnell produziert wird. Falls die Arbeitskräfte per Akkordlohn bezahlt werden, also pro hergestellten Produkt, so ergibt sich für den „Verbrauch“ der Arbeitskräfte ebenfalls ein konstanter Produktionskoeffizient.[11]

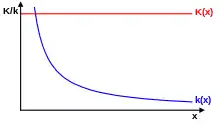
Fallende Produktionskoeffizienten ergeben sich, falls Arbeitskräfte pro Zeit bezahlt werden (Zeitlohn). Je schneller sie arbeiten desto geringer sind dann die Stückkosten. Die gesamten Kosten verlaufen dann waagrecht, also unabhängig davon, wie schnell produziert wird.

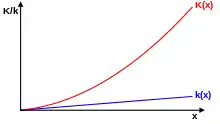
Steigende Produktionskoeffizienten sind typisch für den Verbrauch von Schmiermitteln oder Werkzeugen bei Dreh- oder Fräsmaschinen. Der Verbrauch wird oft in den Ingenieurwissenschaften genauer analysiert. Der Verschleiß von vielen Werkzeugen ergibt sich beispielsweise über die Taylor-Gerade. Auch der Verbrauch von Werkstoffen steigt ab einer gewissen Schwelle, wenn die erhöhte Produktionsgeschwindigkeit zu erhöhtem Ausschuss führt.[12]

Ein u-förmiger Verlauf hat sich für viele Betriebsstoffe als typisch erwiesen. Der Produktionskoeffizient fällt dann zunächst ab, bis er bei $d_{\mathrm {opt} }$ sein Minimum erreicht und dann wieder steigt. Der Verlauf der Stückkosten ist dann ebenfalls u-förmig und die zugehörigen Gesamtkosten s-förmig: Sie steigen zunächst schnell an, dann immer langsamer, bis sie in der Umgebung von $d_{\mathrm {opt} }$ näherungsweise linear steigen. Anschließend steigen sie immer schneller. Wenn man die Stückkosten der einzelnen Faktoren an einer einzelnen Maschine addiert, so ergibt sich häufig auch ein u-förmiger Verlauf. Wenn beispielsweise eine Maschine nur die zwei Faktoren Arbeit (Zeitlohn, also fallende Stückkosten) und Werkzeuge (steigend) benötigt, so sind die gesamten Stückkosten u-förmig. Bei den kombinierten Anpassungen (intensitätsmäßig-quantitativ, intensitätsmäßig-zeitlich und intensitätsmäßig-zeitlich-quantitativ) wird daher im Folgenden immer ein u-förmiger Produktionskoeffizient $a(d)$ zugrunde gelegt.[13]

Rein zeitliche Anpassung

Bei der rein zeitlichen Anpassung sind die Anzahl der Maschinen und ihre Intensität konstant; lediglich ihre Einsatzdauer wird verändert. In diesem Fall sind die Produktionskoeffizienten konstant und es ergeben sich konstante Stückkosten und linear steigende Gesamtkosten – genau wie bei der intensitätsmäßigen Anpassung und konstantem Produktionskoeffizienten. Die Zeit kann nur innerhalb der Grenzen $t_{\mathrm {min} }$ und $t_{\mathrm {max} }$ variiert werden. Die Mindestdauer der Produktion beträgt in der Regel Null, kann aber auch mit der maximalen Dauer identisch sein. Das Anfahren von Kraftwerken und Hochöfen ist beispielsweise so teuer, dass sie normalerweise ununterbrochen im Einsatz sind und nur für Wartungsarbeiten abgeschaltet werden. Die maximale Einsatzzeit kann technisch vorgegeben sein, in der Regel wird sie aber über die vertraglich oder tariflich geregelte Arbeitszeit bestimmt. Für die Maschinen ist die zeitliche Anpassung meist kein Problem: Sie werden nach der gewünschten Dauer einfach abgeschaltet. Arbeitskräfte, die nach Zeitlohn bezahlt werden, müssen aber bezahlt werden, auch wenn sie nicht arbeiten. Eine gewisse Anpassungsmöglichkeit ergibt sich durch den Einsatz von Kurzarbeit und den Abbau von Schichten oder durch Überstunden und zusätzliche Schichten. Möglich sind auch flexible Arbeitszeitmodelle.[14]

Rein quantitative Anpassung

Bei der rein quantitativen Anpassung sind die Intensität und Einsatzdauer aller aktiven Maschinen identisch. Es werden bisher inaktive Maschinen in Betrieb genommen oder aktive abgeschaltet. Der „Verlauf“ der Kostenfunktionen besteht aus einzelnen Punkten. Wenn mit einer einzelnen Maschine die Produktionsmenge $x$ erzeugt werden kann, so sind die Kostenfunktionen nur an den Stellen $x,2x,3x,\dotsc$ definiert. Zu unterscheiden ist jedoch, ob die vorhandenen Maschinen alle dieselben Stückkosten haben (mutative Anpassung) oder verschiedene (selektive Anpassung).[15] In vielen Betrieben werden über viele Jahre hinweg immer wieder neue Maschinen beschafft, sodass neben neueren und in der Regel verbrauchsarmen Maschinen auch noch ältere vorhanden sind mit höherem Verbrauch. Die selektive Anpassung stellt somit den Normalfall dar. In der Regel ist es jedoch ohne weiteres möglich alle Maschinen auch gleichzeitig zeitlich anzupassen, sodass die rein quantitative Anpassung selten ausführlich analysiert wird. Sie wird als Spezialfall der kombinierten zeitlichen und quantitativen Anpassung betrachtet.[16]

Kostenfunktionen kombinierter Anpassungen

Bei den kombinierten Anpassungen werden mindestens zwei oder auch alle drei möglichen Parameter $d,t$ und $m$ gleichzeitig verändert. Es handelt sich somit um Kombinationen der reinen Anpassungen.

Zeitliche und quantitative Anpassung

Gesamtkostenverlauf bei zeitlich-quantitativer Anpassung

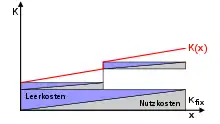
Bei der kombinierten zeitlichen und quantitativen Anpassung wird meist davon ausgegangen, dass in einem Betrieb Fixkosten $K_{\mathrm {fix} }$ anfallen, die unabhängig von der Produktionsmenge sind, wie Mieten für Gebäude, Versicherungsgebühren oder Leasinggebühren für Maschinen. Außerdem fallen für die bloße Inbetriebnahme jeder einzelnen Maschine sogenannte Sprungfixe oder intervallfixe Kosten $K_{fi}$ an.

Bei identischen Maschinen (mutative Anpassung) haben alle Abschnitte der Kostenfunktionen identische Steigung. Die Fixkosten lassen sich in einen Nutzkostenanteil und einen Leerkostenanteil zerlegen der von der Produktionsmenge abhängig ist. Wird die maximal mögliche Produktionsmenge mit $x_{\mathrm {max} }$ und die tatsächliche mit $x$ bezeichnet, so ergeben sich die Leerkosten als:[17]

K_{\mathrm {leer} }={\frac {K_{\mathrm {fix} }}{x_{\mathrm {max} }}}\cdot (x_{\mathrm {max} }-x)

und die Nutzkosten als

K_{\mathrm {nutz} }={\frac {K_{\mathrm {fix} }}{x_{\mathrm {max} }}}\cdot x

Bei Maschinen mit verschiedenen Kostenverläufen ergibt sich ein ökonomisches Auswahlproblem (selektive Anpassung). Kleine Produktionsmengen werden mit der kostengünstigeren Maschine produziert. Erst wenn ihre Kapazität nicht mehr ausreicht wird zusätzlich mit einer weiteren Maschine produziert. Wenn bei einer rückläufigen Produktionsmenge zuerst die kostengünstigere Maschine stillgelegt wird, so verharren die Kosten auf einem höheren Niveau als dies vor Ausweitung der Produktion der Fall war. Dieser Effekt wird als Kostenremanenz bezeichnet. Werden dagegen bewusst Kapazitäten aufgebaut um die Produktionsmenge in Zukunft ausweiten zu können, verursachen diese zusätzlichen Kapazitäten trotzdem schon Kosten. Dieses Phänomen wird als Kostenpräkurenz bezeichnet.[18]

Intensitätsmäßige und zeitliche Anpassung

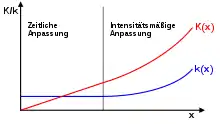
Stück- und Gesamtkosten bei zeitlich-intensitätsmäßiger Anpassung bei der Gutenberg-Produktionsfunktion

Die kombinierte intensitätsmäßige und zeitliche Anpassung wird üblicherweise für den Fall einer einzelnen Maschine und u-förmigen Produktionskoeffizienten betrachtet. Im Folgenden wird vereinfachend davon ausgegangen, dass die Mindesteinsatzdauer $t_{\mathrm {min} }$ und die Mindestintensität $d_{\mathrm {min} }$ jeweils Null betragen. Wegen des u-förmigen Produktionskoeffizienten gibt es eine verbrauchsminimale Intensität $d_{\mathrm {opt} }$ bei der vorzugsweise produziert wird. Kleine Produktionsmengen werden dann immer mit $d_{\mathrm {opt} }$ produziert und die Einsatzdauer an die geforderte Produktionsmenge angepasst. Mit dieser Methode können jedoch maximal $x_{\mathrm {opt} }=d_{\mathrm {opt} }\cdot t_{\mathrm {max} }$ Produkteinheiten hergestellt werden. Falls mehr produziert werden sollt, muss die Intensität bei maximaler Einsatzdauer über $d_{\mathrm {opt} }$ erhöht werden. Insgesamt lässt sich dann festhalten, dass Produktionsmengen die kleiner als $x_{\mathrm {opt} }$ sind, durch rein zeitliche Anpassung bei $d=d_{\mathrm {opt} }$ und $t\leq t_{\mathrm {max} }$ erreicht werden und solche die größer sind durch rein intensitätsmäßige Anpassung bei $t=t_{\mathrm {max} }$ und $d\geq d_{\mathrm {opt} }$ .[19]

Graphisch bedeutet diese Vorgehensweise für den Stückkostenverlauf eine Kombination der reinen Anpassungsformen. Er ist zunächst horizontal wie der Stückostenverlauf bei rein Zeitlicher Anpassung und ab $x=x_{\mathrm {opt} }$ verläuft er steigend wie der Verlauf bei rein intensitätsmäßiger Anpassung. Die Gesamtkosten verlaufen entsprechend zunächst vom Ursprung linear steigend um ab $x_{\mathrm {opt} }$ immer stärker zu steigen.

Intensitätsmäßige, quantitative und zeitliche Anpassung

Verlauf der Grenzkosten zweier Maschinen bei, zeitlich, quantitativ intensitätsmäßiger Anpassung.

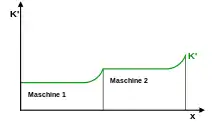
Bei der kombinierten intensitätsmäßigen, quantitativen und zeitlichen Anpassung wird meist davon ausgegangen, dass für die einzelnen Maschinen die Kostenfunktionen für die kombinierte intensitätsmäßige und zeitliche Anpassung bereits bekannt sind. Die Gesamtkosten der einzelnen Maschinen werden dann nach der Produktionsmenge abgeleitet um so zu den Grenzkosten $K'$ zu gelangen

K'={\frac {\mathrm {d} K(x)}{\mathrm {d} x}}

.

Geometrisch lassen sich die Grenzkosten als Steigung der Kostenfunktion interpretieren. Ökonomisch gesehen geben sie für eine bestimmte Produktionsmenge $x$ an um wie viel sich die Kosten $K$ erhöhen wenn eine zusätzliche (infinitesimal kleine) Einheit hergestellt wird. Die Grenzkosten verlaufen grundsätzlich ähnlich wie die Stückkosten bei zeitlicher und intensitätsmäßiger Anpassung.

Grundsätzlich wird auf derjenigen Maschine die Produktionsmenge ausgeweitet, die die geringsten Grenzkosten hat. Sie wird zunächst zeitlich angepasst. Da die Grenzkosten während der zeitlichen Anpassung wegen des konstanten Produktionskoeffizienten nicht steigen, wird die Einsatzdauer erhöht bis die maximale Einsatzdauer erreicht ist. Danach muss intensitätsmäßig angepasst werden, was zu steigenden Grenzkosten führt. Sobald sie die Grenzkosten der zweitgünstigsten Maschine erreicht haben wird diese zeitlich angepasst.[20]

Kritische Würdigung und Weiterentwicklung

Der Gutenberg-Produktionfunktion wird in eine hohe Realitätsnähe nachgesagt, insbesondere für die industrielle Produktion von Stückgütern (Fertigungsindustrie), in geringerem Maße auch für die chemische und die Rohstoffindustrie (Prozessindustrie). Sie wird aber den betrieblichen Möglichkeiten nicht in vollem Umfang gerecht. Sie berücksichtigt nicht den zeitlichen Verlauf der Produktion, sondern nur die Einsatzdauer und auch keine Auftragsreihenfolgen, Losgrößen und substitutionalen Produktionsbedingungen. Letztere sind insbesondere in der chemischen Industrie vorherrschend. Dort führen häufig unterschiedliche Kombinationen von Temperatur und Druck zum selben Ergebnis. Es existieren folglich auch Wahlmöglichkeiten für die Leistungsabgabe des Kompressors (für den Druck) und des Ofens (für die Temperatur). Edmund Heinen hat die genannten Kritikpunkte aufgegriffen und die Gutenberg-Produktionsfunktion erweitert und verfeinert zur Heinen-Produktionsfunktion, die auch als „Produktionsfunktion vom Typ C“ bekannt ist. Außerdem wird kritisiert, dass die Gutenberg-Produktionsfunktion die Inanspruchnahme der Potentialfaktoren (Anlagenverschleiß und menschliche Arbeit) nur unzureichend abbilde. Die als konstant angesehene z-Situation wird ebenfalls bemängelt: Jedes Mal wenn sie sich ändert, müssen neue Verbrauchsfunktionen ermittelt werden. Insgesamt gesehen eignet sie sich deshalb vor allem für die Modellierung des Werkstoffverbrauchs (Energie, Treibstoffe, Werkzeuge, Schmiermittel etc.) in der Fertigungsindustrie.[21]

In den 1960er Jahren beschäftigten sich mehrere Studien mit empirischen Überprüfung der Gutenberg-Produktionsfunktion. 1960 wurde der Zusammenhang zwischen der erzeugten Energie und dem Verbrauch von Dampf einer Dampfturbine[22] ermittelt. 1966[23] wurde der Energieverbrauch von Elektromotoren und der Kohleverbrauch von Dampfkesseln untersucht. 1968 wurde an einer Anlage zur Papiererzeugung[24] der Verbrauch von Wasser und Dampf ermittelt. Bei allen wurde ein von der Intensität abhängiger Produktionskoeffizient festgestellt der meist auch einen u-förmigen Verlauf hatte. Lediglich der Verbrauch der Papieranlage verlief monoton fallend.[25]

Angeregt durch die Arbeiten Karl Poppers zum Kritischen Rationalismus untersuchten 1974 Marcel Schweitzer und Hans-Ulrich Küpper[26] einen Großteil der damaligen Produktionstheorie. Die Gutenberg-Produktionsfunktion stellte sich als widerspruchsfrei und grundsätzlich allgemeingültig heraus – jedenfalls innerhalb der industriellen Produktion für die sie entwickelt wurde. Sie ist auch grundsätzlich empirisch überprüfbar, auch wenn dies im Einzelnen aufgrund von Messproblemen schwierig sein kann. Ihr wurde ein deutlich höherer Bewährungsgrad als anderen Produktionsfunktionen und ein relativ großer Geltungsbereich bescheinigt. Lediglich die fehlende Trennung in Axiome und daraus abgeleitete, logische Folgerungen („Axiomatisierung“) wurde kritisiert.[27]

Parallele Entwicklungen in der Produktionstheorie

Zeitgleich zu den Arbeiten Gutenbergs gab es im angelsächsischen Bereich zwei weitere Entwicklungen der Produktionstheorie:

In der Volkswirtschaftslehre wurde die lineare Aktivitätsanalyse entwickelt. Sie wurde Ende der 1960er Jahre durch Waldemar Wittmann verallgemeinert und wie alle volkswirtschaftlichen Entwicklungen zuvor in die deutsche Betriebswirtschaft übernommen. Die allgemeine Aktivitätsanalyse enthält als Spezialfall dann die Gutenberg-Produktionsfunktion, wie auch alle anderen Produktionsfunktionen.
Im Operations Management, dem angelsächsischen Gegenstück zur Produktionswirtschaft entstanden die Engineering Production Functions. Sie zeichnen sich wie die Gutenberg-Funktion durch eine hohe Praxisorientierung aus, beziehen sich aber auf in der Planung befindliche Produktionsanlagen und nicht auf die Optimierung bereits existierender Betriebe.

Siehe auch

Literatur

Sonntag: Die Gutenberg Produktionsfunktion, Gabler, Wiesbaden, 2004

Einzelnachweise

Wöhe: Einführung in die allgemeine Betriebswirtschaftslehre 25. Auflage, S. 310.
Fandel: Produktion I, 1. Auflage 1987, Springer, Berlin, S. I
Dyckhoff: Betriebliche Produktion Springer, Berlin, 1992, S. 35
Steven: Produktionstheorie Gabler, Wiesbaden, 1998, S. 21f.
Steven: Produktionstheorie Gabler, Wiesbaden, 1998, S. 34f.
Sonntag: Die Gutenberg Produktionsfunktion, Gabler, Wiesbaden, 2004, S. 11
Heinen: Grundfragen der entscheidungsorientierten Betriebswirtschaftslehre In: Schweitzer (Hrsg.): Auffassungen und Wissenschaftsziele der Betriebswirtschaftslehre. Darmstadt 1978, S. 219–246. Zitiert nach: Erich Zahn, Uwe Schmidt: Produktionswirtschaft. Band 1: Grundlagen und operatives Produktionsmanagement. UTB, Stuttgart, ISBN 978-3-8252-8126-7, S. 25. Volles Zitat: „Betriebswirtschaften sind nicht ‚Veranstaltungen‘ irgendwelcher abstrakter Produktionsfaktoren, sondern Sozialsysteme, in denen Menschen unter Verwendung technischer Hilfsmittel arbeitsteilig und kooperativ zur Erreichung des Organisationsziels und eigener Ziele zusammenarbeiten.“
Steven: Produktionstheorie, Gabler, Wiesbaden, 1998, S. 128.
Steven: Produktionstheorie Gabler, Wiesbaden, 1998, S. 130 + 133.
Corsten: Produktionswirtschaft 12. Auflage, S. 145f.
Steven: Produktionstheorie Gabler, Wiesbaden, 1998, S. 145–150.
Steven: Produktionstheorie Gabler, Wiesbaden, 1998, S. 145.
Steven: Produktionstheorie Gabler, Wiesbaden, 1998, S. 145–150.
Steven: Produktionstheorie Gabler, Wiesbaden, 1998, S. 135f.
Corsten: Produktionswirtschaft 12. Auflage, S. 150f.
Steven: Produktionstheorie Gabler, Wiesbaden, 1998, S. 138–143.
Corsten: Produktionswirtschaft 12. Auflage, S. 150f.
Corsten: Produktionswirtschaft 12. Auflage, S. 152
Corsten: Produktionswirtschaft 12. Auflage, S. 153f.
Adam: Produktionsmanagement 9. Auflage, S. 380
Corsten: Produktionswirtschaft 12. Auflage, S. 101
Gälweiler: Produktionskosten und Produktionsgeschwindigkeit 1960
Pack Ermittlung der kostenminimalen Anpassungsprozeßkombination, in: Zeitschrift für betriebswirtschaftliche Forschung 1966, S. 466–476
Pressmar Die Kosten-Leistungs-Funktion industrieller Produktionsanlagen 1968
Fandel: Produktion I 5. Auflage, S. 204–216
Schweitzer M., Küpper H.-U.: Produktions- und Kostentheorie der Unternehmung Reinbek bei Hamburg, 1974
Fandel: Produktion I 5. Auflage, S. 195–198 und 201

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Wöhe: Einführung in die allgemeine Betriebswirtschaftslehre 25. Auflage, S. 310.

[2] Fandel: Produktion I, 1. Auflage 1987, Springer, Berlin, S. I

[3] Dyckhoff: Betriebliche Produktion Springer, Berlin, 1992, S. 35

[4] Steven: Produktionstheorie Gabler, Wiesbaden, 1998, S. 21f.

[5] Steven: Produktionstheorie Gabler, Wiesbaden, 1998, S. 34f.

[6] Sonntag: Die Gutenberg Produktionsfunktion, Gabler, Wiesbaden, 2004, S. 11

[7] Heinen: Grundfragen der entscheidungsorientierten Betriebswirtschaftslehre In: Schweitzer (Hrsg.): Auffassungen und Wissenschaftsziele der Betriebswirtschaftslehre. Darmstadt 1978, S. 219–246. Zitiert nach: Erich Zahn, Uwe Schmidt: Produktionswirtschaft. Band 1: Grundlagen und operatives Produktionsmanagement. UTB, Stuttgart, ISBN 978-3-8252-8126-7, S. 25. Volles Zitat: „Betriebswirtschaften sind nicht ‚Veranstaltungen‘ irgendwelcher abstrakter Produktionsfaktoren, sondern Sozialsysteme, in denen Menschen unter Verwendung technischer Hilfsmittel arbeitsteilig und kooperativ zur Erreichung des Organisationsziels und eigener Ziele zusammenarbeiten.“

[8] Steven: Produktionstheorie, Gabler, Wiesbaden, 1998, S. 128.

[9] Steven: Produktionstheorie Gabler, Wiesbaden, 1998, S. 130 + 133.

[10] Corsten: Produktionswirtschaft 12. Auflage, S. 145f.

[11] Steven: Produktionstheorie Gabler, Wiesbaden, 1998, S. 145–150.

[12] Steven: Produktionstheorie Gabler, Wiesbaden, 1998, S. 145.

[13] Steven: Produktionstheorie Gabler, Wiesbaden, 1998, S. 145–150.

[14] Steven: Produktionstheorie Gabler, Wiesbaden, 1998, S. 135f.

[15] Corsten: Produktionswirtschaft 12. Auflage, S. 150f.

[16] Steven: Produktionstheorie Gabler, Wiesbaden, 1998, S. 138–143.

[17] Corsten: Produktionswirtschaft 12. Auflage, S. 150f.

[18] Corsten: Produktionswirtschaft 12. Auflage, S. 152

[19] Corsten: Produktionswirtschaft 12. Auflage, S. 153f.

[20] Adam: Produktionsmanagement 9. Auflage, S. 380

[21] Corsten: Produktionswirtschaft 12. Auflage, S. 101

[22] Gälweiler: Produktionskosten und Produktionsgeschwindigkeit 1960

[23] Pack Ermittlung der kostenminimalen Anpassungsprozeßkombination, in: Zeitschrift für betriebswirtschaftliche Forschung 1966, S. 466–476

[24] Pressmar Die Kosten-Leistungs-Funktion industrieller Produktionsanlagen 1968

[25] Fandel: Produktion I 5. Auflage, S. 204–216

[26] Schweitzer M., Küpper H.-U.: Produktions- und Kostentheorie der Unternehmung Reinbek bei Hamburg, 1974

[27] Fandel: Produktion I 5. Auflage, S. 195–198 und 201