Kostenfunktion (Wirtschaft)
Eine Kostenfunktion stellt innerhalb der Wirtschaftswissenschaften den Zusammenhang zwischen den Kosten und einer Bezugsgröße dar.
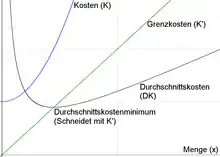
Die erste Ableitung der Kostenfunktion bezeichnet man als Grenzkosten.
Arten von Kostenfunktionen
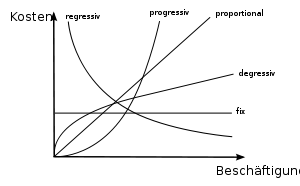
Abhängig von ihrem Verlauf werden folgende Kostenfunktionen unterschieden:
- proportional (linear)
- Die Kosten ändern sich im selben Verhältnis wie die Bezugsgrößenmenge. Die Stückkosten bleiben dann – unabhängig von der Bezugsgrößenmenge – konstant und sind identisch mit den Grenzkosten.
- degressiv (unterproportional)
- Die Kosten nehmen bei steigender Bezugsgrößenmenge langsamer zu. Die Stückkosten verringern sich somit bei zunehmender Ausbringungsmenge. Das kann z. B. an Nachlässen liegen, die bei hoher Mengenabnahme gewährt werden. Ein anderes Beispiel wäre, dass die Produktionszeit durch einen Lernkurven-Effekt abnimmt, d. h. der dritte produzierte PC wird schneller hergestellt als der erste.
- progressiv (überproportional)
- Die Kosten nehmen bei steigender Bezugsgrößenmenge stärker zu. Die Stückkosten steigen dabei an (z. B. aufgrund von Überstunden).
- regressiv (abnehmend)
- Die Kosten und auch deren Stückkosten nehmen bei steigender Bezugsgrößenmenge ab (z. B. Heizkosten in Veranstaltungsräumen bei steigender Besucherzahl).
- fix
- Die Kosten bleiben unabhängig von der Ausprägung der Bezugsgröße konstant. Die Stückkostenfunktion verläuft degressiv (siehe auch Fixkostendegression). Die Grenzkosten sind 0.
- sprungfix
- Die Kosten bleiben auf bestimmten Intervallen der Bezugsgrößenmenge konstant. Zwischen diesen Intervallen „springen“ die Kosten auf ein anderes Niveau. Die Kostenfunktion nimmt einen treppenartigen Verlauf an.
Reziprok
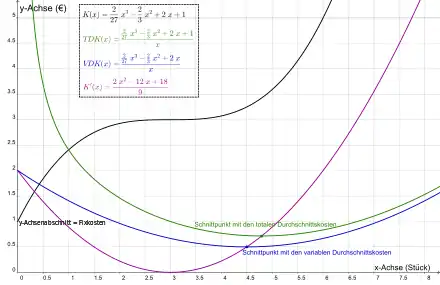
Der Graph verläuft in eine r-l-Wendekurve (reziprok „s-förmige“/ degressiv-progressiv-Funktion) und ist ein nichtlinearer Kostenverlauf wie im gleichnamigen Bild (schwarzer Graph)
Überblick
| Verlauf | allgemeine Form | Beispiel | Grenzkosten | Stückkosten |
|---|---|---|---|---|
| proportional | ||||
| degressiv | ||||
| progressiv | ||||
| regressiv | ||||
| fix | ||||
| sprungfix | , in den Sprungstellen |
Hierbei gilt
- : Kostenfunktion
- : Bezugsgrößenmenge
- und : Konstanten. Für degressive Kosten gilt zusätzlich .
Erklärung der Grafik Nichtlinearer Kostenverlauf
Die totalen Durchschnittskosten sinken zunächst, weil die Mehrproduktion Kostenvorteile bringt. Dabei müsste die Stückzahl-Quantifizierung am besten als Output je Zeiteinheit gedeutet werden. Damit könnte erklärt werden, weshalb die totalen Durchschnittskosten später vorübergehend wieder ansteigen: Es braucht wegen Erreichens der Produktions-Kapazitätsgrenze eine Erweiterungs-Investition, deren Kosten auf die totalen Durchschnittskosten umgelegt werden. Dass die Grenzkosten-Kurve die Durchschnittskosten-Kurven in ihrem Minimum durchschneidet, wird dadurch erklärt, dass, solange der Kostenzuwachs der letzten Einheit kleiner ist als die Durchschnittskosten aller vorherigen, dieser Zuwachs den Durchschnitt aller vorherigen Zuwächse, in den er einbezogen ist, nach unten drückt. Sobald GK = DK ist, kann der Durchschnitt nicht mehr gedrückt werden und wird dann künftig angehoben.[1]
Siehe auch
Weblinks
Einzelnachweis
- P. A. Samuelson: Volkswirtschaftslehre, Band 2