Ertragsgesetz
Das Ertragsgesetz (auch Gesetz des sinkenden Grenzertrags oder Gesetz vom abnehmenden Ertragszuwachs) ist ein ökonomisches Modell, das die Relation von Aufwand/Einsatz (englisch Input) und Ertrag (englisch Output) beschreibt, wenn ein Produktionsfaktor verändert wird und alle anderen gleich bleiben (partielle Faktorvariation).
Allgemeines
Außerhalb der Rechtswissenschaft (hier gibt es formale Gesetze) spricht man in den übrigen Wissenschaften von einem Gesetz, wenn aus einer Theorie orts-, zeit- und kulturunabhängige allgemeingültige Aussagen abgeleitet werden, die weltweit dauerhaft gelten. Gesetze sind in der Naturwissenschaft ausnahmslos geltende Regeln für den Ablauf des Geschehens.[1] Das Ertragsgesetz beruht auf Naturgesetzen, die globale Geltung besitzen, ist jedoch nach Paul Samuelson und William Nordhaus von diesen zu unterscheiden: „Das Ertragsgesetz ist eher eine weithin beobachtete empirische Gesetzmäßigkeit als eine universelle Wahrheit, wie wir sie etwa dem Gesetz der Schwerkraft zubilligen“[2].
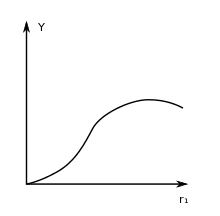
Es wurde ursprünglich von Anne Robert Jacques Turgot für die Landwirtschaft als Bodenertragsgesetz definiert: Erhöht man auf dem gleichen Stück Boden stetig den Arbeitseinsatz, so nimmt der Ertrag zunächst schnell zu, dann nur noch langsam, dann bleibt er gleich, und schließlich nimmt er sogar wieder ab.[3] Dieses Gesetz gilt nicht nur in der Agrarproduktion, sondern auch in der Industrieproduktion und in anderen Bereichen.[4]
Beispiel
Wird für das Produkt X oder die Partei Y bisher kaum oder wenig geworben und nun der Werbeaufwand stark erhöht, dann wachsen die Umsatzerlöse bzw. die Stimmanteile zunächst progressiv an. Ab einem bestimmten Punkt wachsen sie nur noch degressiv, bis sie schließlich asymptotisch gegen Null tendieren. Dieser Trend lässt sich bei gleichbleibender Qualität auch durch noch so großen Aufwand nicht mehr umkehren.
Begriffliche Abgrenzung
Das Ertragsgesetz im eigentlichen Sinn, auch klassisches Ertragsgesetz genannt, beschreibt eine Technologie, bei der durch Vermehrung eines Faktors (c. p.) die Produktmenge zunächst überproportional, von einem gewissen Punkt an unterproportional zunimmt und schließlich absolut abnimmt. Diese Gesetzmäßigkeit wird in 4 Phasen eingeteilt (siehe Abschnitt Ertragsgesetz#Ertragsgesetzliche Produktionsfunktion) und trägt damit den breiteren Bedeutungsinhalt.
Im engeren Sinn verstanden schon die Klassiker, dass die erste Phase für die Produktion meist irrelevant ist. So spricht man oft von der Unterscheidung in klassisches und neoklassisches Ertragsgesetz. Mit dem neoklassischen Ertragsgesetz sind nun die Phasen 2 und 3 gemeint (auch neoklassischer Bereich oder sogar neoklassische Produktionsfunktion). Diese sind für die mikroökonomische Unternehmenstheorie von besonderem Interesse, weil nur hier für ein Konkurrenzunternehmen (Polypol) Gewinnmaximierung möglich ist.[5] Das Ertragsgesetz der neoklassischen Produktionstheorie unterstellt also von Anfang an positive und abnehmende Grenzerträge (neoklassische Produktionsfunktion).[3] In diesem Bereich steigt mit jeder zusätzlich eingesetzten Produktionsfaktor-Mengeneinheit der Gesamtertrag, der Grenzertrag ist noch immer positiv, liegt aber wertmäßig bereits unter dem Durchschnittsertrag.[6]
Oft wird die Kurzform Ertragsgesetz im Deutschen irreführend[7] verwendet, da hier eigentlich nicht das Ertragsgesetz als Ganzes, sondern nur der spezielle interessierende Ausschnitt – die neoklassische Produktionsfunktion – gemeint ist. Auch können andere Kurvenverläufe einen „ertragsgesetzlichen“ Zusammenhang zwischen Fakteinsatzmengen und Erträgen zeigen.[8] Es gibt auch ertragsgesetzliche Kostenfunktionen.
Eindeutiger ist die Bezeichnung Gesetz vom abnehmenden Grenzertrag oder Gesetz vom abnehmenden Ertragszuwachs (bei Einsatz eines variablen Faktors, d. h. ceteris paribus).
Es handelt sich also eher um qualitative Unterschiede in der Beschreibung ein und desselben Sachverhaltes. Das Ertragsgesetz ist weder eine Regel im Sinne einer juristischen Norm noch bezeichnet es eine Regel im Sinne einer unbedingten wissenschaftlichen Methode.
Geschichte
Das klassische Ertragsgesetz gilt als älteste Produktionsfunktion.[9] Als seine „Entdecker“ gelten unabhängig voneinander Turgot, Thünen, Denham-Steuart und Malthus, die aus verschiedenen Ansätzen heraus zu vergleichbaren Beschreibungen kamen.
- Anne Robert Jacques Turgot[3][10]
- Turgot war französischer Staatsmann und Ökonom der Aufklärung. Durch Beobachtung der landwirtschaftlichen Produktion gelangte er 1767/68 zu der Erkenntnis, dass, wenn man sonst alle Faktoren konstant hält (z. B. Größe der Ackerfläche, Menge des Saatguts und Düngers), mit zunehmendem Einsatz von Arbeit zunächst mit steigenden, aber ab einem gewissen Punkt mit abnehmendem Ertragszuwachs zu rechnen ist.[11][12]
- Johann Heinrich von Thünen
- Thünen sammelte auf seinem Gut in Mecklenburg statistisches Material, um daraus Schlüsse über die vernünftige Leitung eines landwirtschaftlichen Gutes zu ziehen.[13] Damit konnte er 1842 die von Turgot beobachtete Gesetzmäßigkeit statistisch nachweisen und formalisieren.[11]
„Es liegt "in der Natur des Landbaues – und dies ist ein sehr beachtungswerter Umstand – daß das Mehrerzeugnis nicht in geradem Verhältnis mit der Zahl der mehr angestellten Arbeiter steigt, sondern jeder später angestelle Arbeiter liefert ein geringeres Erzeugnis als der vorhergehende …"“
- Man kann festhalten, dass schon Thünen (1850) nicht das klassische Ertragsgesetz im weiten Sinne meinte. Wahrscheinlich schloss er anfängliche Effizienzsteigerung aus, da man ein Gut mit nur einigen wenigen Arbeitern nicht sinnvoll führen kann.
Ertragsgesetzliche Produktionsfunktion
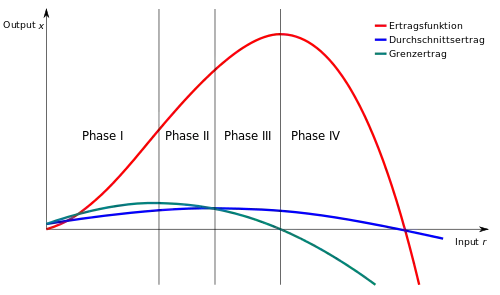
Plausibilität besitzt das klassische Ertragsgesetz über seinen gesamten Verlauf (eigentlich nur) für landwirtschaftliche Produktionsprozesse bei partieller Faktorvariation. Gleichwohl wird es ebenso als Ertragskurve bei totaler Faktorvariation und für andere Produktionsprozesse herangezogen. Der Grund dafür ist sein hohes didaktisches Potential. Das Diagramm zeigt sowohl Bereiche zu- als auch abnehmender Grenzerträge. Die Stelle des Wechsels von zunehmenden zu abnehmenden Grenzerträgen (Wendestelle) wird als (erste) „Schwelle“ bezeichnet, da ab dort die Ertragszuwächse fallen. Die Wendestelle ist gleich der Minimalstelle der Grenzkosten, die als weitere (zweite) Schwelle bezeichnet wird. Beim klassischen Ertragsgesetz besitzen die durchschnittlichen Erträge dort ein Maximum, wo die Produktionselastizität eins ist, d. h. die Grenzerträge gleich den Durchschnittserträgen sind.
Der Funktionsgraph erinnert an die Gestalt eines nach rechts geneigten S. In der Betriebswirtschaftslehre ist der Verlauf auch als ertragsgesetzliche Produktionsfunktion oder Produktionsfunktion vom Typ A bekannt. Der Mehreinsatz eines Produktionsmittels bei Konstanz der übrigen Produktionsfaktoren bringt zuerst zunehmende Ertragszuwächse (Grenzerträge oder Grenzprodukte), dann von einer bestimmten Einsatzmenge an abnehmende und schließlich sogar negative Grenzerträge.
Phase I
Der erste Abschnitt ist durch eine überproportionale Steigung der Ertragsfunktion gekennzeichnet. Grenz- und Durchschnittsertrag steigen ebenfalls, jedoch ist die Phase I durch die Maximalstelle der Grenzertragsfunktion begrenzt. Mathematisch ist dies zu ermitteln, indem man die 2. Ableitung der Ertragsfunktion gleich Null setzt.
Phase II
Der zweite Abschnitt ist durch eine annähernd proportionale Steigung der Ertragsfunktion gekennzeichnet (verursacht durch annähernd konstante Grenzerträge). Die Grenzertragsfunktion sinkt bereits wieder, während die Durchschnittsertragsfunktion noch steigt. Phase II ist durch die Maximalstelle der Durchschnittsertragsfunktion begrenzt. Mathematisch ist dies zu ermitteln, indem man den Durchschnittsertrag mit dem Grenzertrag gleichsetzt.
Phase III
Der dritte Abschnitt ist durch eine unterproportionale Steigung der Ertragsfunktion gekennzeichnet. In dieser Phase sinkt sowohl die Grenzertragsfunktion als auch die Durchschnittsertragsfunktion. Begrenzt ist die Phase III durch die Maximalstelle der Ertragsfunktion. An dieser Intervallgrenze schneidet die Grenzertragsfunktion die Abszisse. Mathematisch lässt sich dies ermitteln, indem man die 1. Ableitung der Ertragsfunktion gleich Null setzt.
Phase IV
Im vierten Abschnitt weisen Ertrags-, Grenz- und Durchschnittsertragsfunktion eine negative Steigung auf.
Beispiele
In der Landwirtschaft lässt sich das funktional (auch nach dem französischen Ökonom J. Turgot und dessen Turgotschem Ertragsgesetz) am Beispiel der Verwendung von Dünger aufzeigen: Durch den kontinuierlich gesteigerten Gebrauch von Düngemitteln (bei sonst gleich bleibenden Ressourcen/Bedingungen (ceteris paribus), also z. B. gleichbleibender Fläche) wächst der Ertrag zunächst stetig an. Der Ertragszuwachs je zusätzlich ausgebrachter Düngemittelmenge nimmt ab einer bestimmten Ausbringungsmenge ab. Dies führt bei weiterer Düngerausbringung schließlich sogar zu einer Gesamtertragsminderung und sogar zur Bodenvergiftung: Ein überhöhter Einsatz von Düngemitteln wird den Ertrag unter das Niveau führen, das ohne Düngemittel erreicht worden wäre, und schließlich jeden Ertrag vernichten. Ähnliche Beobachtungen können auch bei den Faktoren Wärme und Wasser gemacht werden.
Diese Beobachtungen gehen auch auf Eilhard Alfred Mitscherlich zurück, der Das Gesetz vom Minimum und das Gesetz des abnehmenden Bodenertrages mit entsprechenden Verlaufsdiagrammen im Jahre 1909 publizierte.
Am Beispiel der industriellen Produktion oder in der Verwaltung lässt sich das Ertragsgesetz auf den gesteigerten Einsatz von Personal bei sonst gleich bleibenden Rahmenbedingungen ebenfalls beobachten: Je größer die Anzahl von Mitarbeitern ist, desto größer ist der Kommunikations- und Abstimmungsbedarf und desto kleiner ist der pro Person verfügbare Arbeitsplatz (mehrere Mitarbeiter müssen sich Maschinen bzw. Schreibtische, Computer etc. teilen).[14] Es können Situationen erreicht werden, wo sich Mitarbeiter gegenseitig nur noch im Weg stehen oder sich demotivieren. Mehr bewegt wird allein durch die Personalvermehrung also nicht. Ein Staat, der seine Wirtschaft zentralistisch steuert und Arbeitnehmer den Produktionsanlagen zuteilt, ohne diese anzupassen, um so das Problem der Arbeitslosigkeit zu vermeiden, kann seine Produktivität auf diese Art kaum steigern.
Das klassische Ertragsgesetz ist nicht notwendig für die Begründung eines (kurzfristigen) ertragsgesetzlichen Kostenverlaufs, der zu u-förmigen Durchschnittskostenverläufen führt. Diese können auch bei durchgängig abnehmenden Ertragszuwächsen als Folge des Zusammenspiels von steigenden Grenz- und sinkenden durchschnittlichen Fixkosten auftreten.
Literatur
- Günter Fandel: Produktion. Band 1: Produktions- und Kostentheorie. 7. Auflage. Springer, Berlin u. a. 2007, ISBN 978-3-540-73140-5, S. 191f. Kapitel.
- Günter Wöhe, Ulrich Döring: Einführung in die Allgemeine Betriebswirtschaftslehre. 24. überarbeitete und aktualisierte Auflage. Vahlen, München 2010, ISBN 978-3-8006-3795-9, S. 396f. Abschnitt „Ertragsgesetzliche Produktionsfunktion“.
Weblinks
- Ertragsgesetz – Definition im Gabler Wirtschaftslexikon
- Ertragsgesetz – Definition beim Lexikon der Bundeszentrale für politische Bildung
- Das Gesetz vom abnehmenden Ertragszuwachs – Definition im ONPULSON-Lexikon (Fachportal für Entscheider im Mittelstand)
- Das klassische Ertragsgesetz – Artikel (bei mikrooekonomie.de)
- Klassisches Ertragsgesetz – Beispiel sowie Übersetzung eines Auszugs der Arbeit von Turgot (private Seite von Lydia und Karlheinz Korbmacher)
Einzelnachweise
- Max Apel/Peter Ludz, Philosophisches Wörterbuch, 1958, S. 110
- Paul Samuelson, William Nordhaus: Volkswirtschaftslehre. Das internationale Standardwerk der Makro- und Mikroökonomie. 6. Auflage. 2017, ISBN 978-3-89879-379-7, S. 176.
- Ertragsgesetz – Definition im Gabler Wirtschaftslexikon
- Ertragsgesetz – Definition auf juramagazin.de
- Wolfgang Cezanne: Allgemeine Volkswirtschaftslehre, Oldenbourg Wissenschaftsverlag; Auflage: überarbeitete Auflage (14. März 2005), ISBN 3486577700, S. 115
- Neoklassische Produktionsfunktionen (Memento des Originals vom 3. Juli 2011 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis. – kurzer VWL-Artikel
- Vergleich hierzu: Paul Anthony Samuelson, William D. Nordhaus: Volkswirtschaftslehre. Das internationale Standardwerk der Makro- und Mikroökonomie, mi-Fachverlag; Auflage: N.-A. (November 2005), ISBN 3636030337, Seite 164: Das Ertragsgesetz besagt, dass wir laufend geringere zusätzliche Erträge erhalten, wenn wir einen Input bei unveränderten sonstigen Faktoren immer weiter erhöhen.
- Arthur Woll: Allgemeine Volkswirtschaftslehre. Vahlen Franz GmbH; Auflage: 12., 1996, ISBN 3800629739, Seite 174f
- Günter Wöhe/Ulrich Döring: Einführung in die Allgemeine Betriebswirtschaftslehre, Vahlen; Auflage: 24., überarbeitete und aktualisierte Auflage. (13. September 2010), ISBN 3800637952, S. 396
- Ertragsgesetz – Definition beim Lexikon der Bundeszentrale für politische Bildung
- Bernd Schiemenz, Olaf Schönert: Entscheidung und Produktion, Oldenbourg Wissenschaftsverlag; Auflage: überarbeitete Auflage (23. März 2005), ISBN 3486577166, S. 106
- Horst Siebert, Oliver Lorz: Einführung in die Volkswirtschaftslehre, Kohlhammer; Auflage: 15., vollst. überarb. Aufl. (Mai 2007), ISBN 3170194372, S. 72
- Winfried Reiß: Mikroökonomische Theorie: Historisch fundierte Einführung, Oldenbourg Wissenschaftsverlag; Auflage: 6,. vollst. überar. u. verb. A (1. September 2007), ISBN 3486585444, Seite 90f
- Nicholas Gregory Mankiw, Mark Taylor: Grundzüge der Volkswirtschaftslehre. 7., überarbeitete Auflage. Stuttgart 2018, ISBN 978-3-7910-4142-1, S. 177.