LMS-Farbraum
Der LMS-Farbraum ist der für jeden menschlichen Betrachter von Farblichtern oder gefärbten Flächen wirksame Farbraum. Er ist eine physikalisch-mathematische Darstellung des zugrunde liegenden biologisch-psychologischen Prozesses der Farbwahrnehmung. Der LMS-Farbraum ist der eigentliche Zapfenfarbraum und Grundlage für naturgetreu farbwiedergebende technische Systeme.
Die Kürzel
Bedeutung
Die Farbrezeptoren bzw. Zapfen jedes Auges haben eine individuelle spektrale Empfindlichkeit. Diese wird im Wahrnehmungsprozess zu einem bestimmten Sinneseindruck im Nervensystem geformt. Dies gilt für jedes Auge, egal ob tierisch oder menschlich, und den nachfolgenden Nervenapparat.
Jeder normalfarbsichtige Mensch besitzt drei Arten farbempfindlicher Zapfen. Diese werden nach der Lage des Maximums ihrer Empfindlichkeit als L-, M- und S-Zapfen bezeichnet, in deutschsprachiger Literatur wird für S-Zapfen mitunter auch K-Zapfen gesetzt:
- die L-Zapfen nehmen vorrangig den Farbreiz der Strahlung aus dem langwelligen Rotbereich wahr (engl. long wavelength)
- die M-Zapfen den mittleren Grünbereich (engl. medium wavelength)
- die S-/K-Zapfen den kurzwelligen Blaubereich des Spektrums (engl. short wavelength).
Zum Empfangssystem des Sehsinns gehören auch noch die Stäbchen, englisch: rods.
Alternative Kürzel
| nach Zapfenart bzw. Wellenlänge der aufgenommenen Strahlung |
nach Lage des Empfindungsmaximums* |
mit griechischen Buchstaben |
nach Farbenfehlsichtigkeit bzw. ausgefallenem Farbrezeptor (Zapfen) |
|---|---|---|---|
| L (long) | R (bei Rot / red) | ρ (rho) | P (Protanopie) |
| M (medium) | G (bei Grün / green) | γ (gamma) | D (Deuteranopie) |
| S (short) bzw. K (kurz) | B (bei Blau / blue) | β (beta) | T (Tritanopie) |
'*) kann zu Verwechslungen mit den Koordinaten des RGB-Farbraumes führen.
Theorie
Jegliche Farben lassen sich (für einen menschlichen Betrachter) nach dem ersten Grassmannschen Gesetz durch drei Grundfarben darstellen. Deshalb lässt sich jeder Farbnuance in einem dreidimensionalen Vektorraum ein Farbort zuordnen. Diese Betrachtungsweise ist die abstrahierte Symbolik, die für farbgebende Methoden, die Farbmetrik und technische Behandlung von Farben, wie etwa die Farbwiedergabe dieses Bildschirms, notwendig wurde. Farbräume sind an unterschiedliche Aufgaben angepasst und als CIE-Normfarbraum, RGB-Farbraum, CMYK-Farbraum oder LAB-Farbraum in Benutzung.
Eine Strahlung im sichtbaren Bereich direkt von einer Lichtquelle oder indirekt von einer Oberfläche übt einen Farbreiz aus. Dieser verursacht in den drei Zapfen des menschlichen Sehorgans eine Farbvalenz, einen Farbwert. Im nachfolgenden Vorgang im Körper wird dies als Farbton wahrgenommen. Für die „stimulierte“ Reaktion der Farbzentren ist der Begriff Tristimulus gebräuchlich, obwohl dieser Begriff auch für die abgewandelten Normvalenzen genutzt wird.
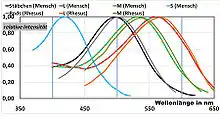
Zur Illustration sind die „Spektralvalenzen“ der Zapfen im Diagramm dargestellt. Die Werte wurden unmittelbar an menschlichen L-, M- und S-Zapfen sowie an menschlichen Stäbchen mit einem Mikroskop-Spektrometer gemessen.[1] Zusätzlich sind die Messwerte an Rhesusaffen eingetragen, die von Bowmaker durchgeführt wurden.[2]
Trotz individueller Unterschiede in den spektralen Absorptionseigenschaften dieser Zapfen, die etwa durch genetische Variationen entstehen, und dem spezifischen Einfluss von Linse oder Glaskörper im Auge, der durch persönliche Färbung oder etwa im Alter durch Trübung bestimmt wird, stimmen die Absorptionskurven für alle normalsichtigen Menschen gut überein.
Die Gesamtheit der wahrnehmbaren Farbreize, also der Farben, wird letztlich auf diese drei Größen L, M und S abgebildet. In der „objektiven Welt“ sind es spektrale Verteilungen, die bei jeder (sogar kontinuierlich gestuften) Wellenlänge zwischen etwa 380 nm und 780 nm Farbreizen mit je einer Intensität von 0 % bis 100 % entsprechen.
Mathematische Beschreibung
Es lässt sich ein dreidimensionaler Vektorraum bilden, der von den drei Achsen L, M, S aufgespannt wird:
- (... ersatzweise auch )
Der eingestrahlte, das Auge treffende Farbreiz hat die spektrale Zusammensetzung f(λ), die aufnehmenden Zapfen absorbieren mit den Spektralwerten l(λ), m(λ) und s(λ). Diese (Zapfen-)Spektralwerte sind die Farbwerte in den Farbgleichungen und ergeben die spektralen Farbvalenzen:
Je nach Interpretation erhält man die ans Nervensystem geleitete Farbvalenz mit den notwendigen drei Farbwerten oder den Farbort der Farbe im Farbraum.
Eine Spektralfarbe ist in der Farbmetrik ein ausreichend schmaler Ausschnitt des elektromagnetischen Spektrums mit der Bandbreite Δλ fast 0 nm, in der Praxis kann diese Breite minimal 1 nm sein.
Lage in der Farbtafel
Da die Empfindlichkeitskurven der Zapfen des menschlichen Auges grundsätzlich keine negativen Zahlenwerte annehmen können, müssen auch die drei Spektralwertfunktionen des LMS-Systems ausschließlich nichtnegative Werte aufweisen.
Dies ist nur möglich, wenn alle Spektralfarben (und damit alle anderen reellen Farben) ausschließlich durch innere Mischung aus den Grundvalenzen , , ermischbar sind. Die drei Grundvalenzen müssen folglich ein Gamut-Dreieck aufspannen, welches den Spektralfarbenzug vollständig umschließt, selbst also außerhalb des Spektralfarbenzugs liegen. Es handelt sich daher (ähnlich wie bei den Normvalenzen) um virtuelle Primärvalenzen.
Jede von ihnen entspricht jener Farbvalenz, welche die zugehörige Farbrezeptor-Art „sehen“ würde, wenn sie allein gereizt würde. Wegen der Überlappung der Empfindlichkeitsbereiche ist es jedoch nicht möglich, eine Rezeptorart allein zu reizen, und keine der Grundvalenzen kann reell erzeugt werden.
Geschichtliches
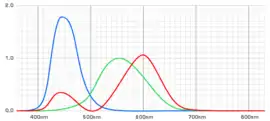
dies sind die Tristimuluskurven in X,Y,Z
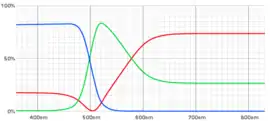
Die Absorptionsspektren L(λ), M(λ) und S(λ) individuell zu messen ist aufwändig. Die Grundsteine für die CIE-Systeme legten die Messungen und Arbeiten von Maxwell, König, Dieterici und Abney, die 1922 von der OSA (Optical Society of America) zusammengefasst und in bearbeiteter Form veröffentlicht wurden.
Da zu dieser Zeit die Möglichkeiten und die Genauigkeit der Messungen unzulänglich waren, führten David Wright (1928) und John Guild (1931) unabhängig voneinander neue und genauere Mischungsversuche (color matches) sowie fotometrische Vergleiche durch und schufen so eine neue Datenbasis. Ihre beiden Datensätze stimmten sehr gut miteinander überein und bestätigten im Rahmen der Genauigkeit auch die älteren Messungen. 1931 wurden Wrights und Guilds Daten von der CIE international als Datenbasis empfohlen.
Stiles, Burch und Speranskaya lieferten später weitere Daten, die ebenfalls die Messungen von Wright und Guild bestätigten und das System erweiterten.[3]
Bowmaker führte schließlich mit einem Mikroskop-Spektrometer direkt am Objekt Messungen zu den Absorptionseigenschaften der Zapfen durch. Dabei zeigte sich, dass die bisher nur indirekt berechenbaren LMS-Empfindlichkeiten sehr gut mit den Messergebnissen, also den tatsächlichen Werten, übereinstimmten.
Da der originäre LMS-Farbraum für technische Zwecke einige Nachteile enthält, wurden die Zapfenvalenzen LMS durch die virtuellen Normvalenzen XYZ ersetzt und der CIE-Norm 1931 zugrundegelegt.
Bis heute wird als weiterer Nachteil und potentielle Fehlerquelle angesehen, dass die Zahl der Individuen aus den messtechnischen Gründen der 1930er Jahre auf 17 ausgesuchte Personen begrenzt war und Guild nur an 7 von ihnen selbst Messungen durchgeführt hatte. Dennoch hat Stiles 1955 bei nachfolgenden Messungen festgestellt, dass die Daten der 17 Personen eine angemessene Repräsentation des 2°-Standardbeobachters darstellen und gewährleisten.[4] Da sich aber heute die CIE-Normwerte durchgesetzt haben, wird vorwiegend mit Transformationen wie dem DIN99-Farbraum unter Nutzung der Rechentechnik korrigiert.
Zur Berücksichtigung aller normalsichtigen Beobachter, die vom Standardbeobachter abweichen, gibt es Datensätze, welche die CIE-Daten ergänzen (standard deviate observer, Standardabweichungs-Beobachter) und die sowohl für den 2°- als auch für den 10°-Standardbeobachter gelten.[5]
Literatur
- Manfred Richter: Einführung in die Farbmetrik. Walter de Gruyter, Berlin 1976.
Einzelnachweise
- Dem Diagramm liegen die Messwerte von Bowmaker und Mollon zu Grunde, die 1983 veröffentlicht wurden.
- Dem Diagramm liegen die Messwerte von Bowmaker aus dem Jahr 1983 zu Grunde.
- David L. MacAdam: Color Measurement 2. ed. Springer-Verlag - Kap. 1.4 „Color Specification in Terms of Equivalent Stimuli“
- R. W. G. Hunt: Measuring Colour. Ellis Horwood Ltd. 1987 - S. 44
- R. W. G. Hunt: Measuring Colour, Ellis Horwood Ltd. 1987. - Tabelle 7.1 „Modifications of CIE colour-matching functions to obtain a standard deviate observer“
