Graßmannsche Gesetze

In den vier graßmannschen Gesetzen der Farbenlehre fasste der Gymnasialprofessor, Mathematiker und Sanskritist Hermann Günther Graßmann (1809–1877) seine Beobachtungen zur Beschreibung und Farbmischung der Farben zusammen. Die von Graßmann aufgestellten Gesetze bezogen sich weitestgehend auf die additive Farbmischung, gelten aber auch grundlegend bei der subtraktiven Farbmischung.

Bedeutung

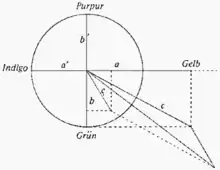
Die Postulate gelten nicht universell für alle sehenden Lebewesen, sondern speziell für den menschlichen Sehsinn. Die Gesetze präzisieren die allgemeine Aussagekraft der Trichromasie. Sie ermöglichen es, exakte Vorhersagen über den zu erwartenden Gleichheitseindruck von Farben zu machen[1] und stellen somit die Grundlage der Farbmetrik dar, mit deren Hilfe beispielsweise die Farbreproduktion im Druck oder die Wiedergabe auf Monitoren vereinheitlicht wird. Ganz allgemein erlaubt diese Lehre von den Maßbezeichnungen der Farben eine Beschreibung der Farbvalenz mit grafischen Mitteln, wie es im Bild rechts auf einem Diagramm der graßmannschen Farbmischungsberechnung mit Hilfe von Vektoren dargestellt ist. Diese Art der Berechnung geht ebenfalls fundamental auf die Arbeiten Graßmanns zurück.

Erste Veröffentlichung

Als Hermann Ludwig Ferdinand von Helmholtz um 1850 seine Dreifarbentheorie auf Grundlage einer älteren Theorie von Thomas Young zur Farbwahrnehmung entwickelte, fand das unter zahlreichen Wissenschaftlern des 19. Jahrhunderts Beachtung. Graßmann fußte seine Überlegungen auf Theorien von Sir Isaac Newton, die dieser in seinem Werk „Opticks: or, a treatise on the reflexions, refractions, inflexions and colours of light“ (London 1704) entwickelt hatte.

In Auseinandersetzung mit einigen fehlerhaften Schlussfolgerungen Helmholtz' (1852), die dieser nach Erscheinen der graßmannschen Arbeit korrigierte, präzisierte Graßmann die Farbentheorie Newtons und verfeinerte diese gerade in Hinsicht auf eine Beschreibung in einem Farbraum deutlich. Im Februar 1853 veröffentlichte er einen Artikel in „Poggendorffs Annalen der Physik und Chemie“.

Die Schrift mit dem Titel „Zur Theorie der Farbenmischung“ beginnt mit den folgenden Worten:

„Hr. Helmholtz [theilt] eine Reihe zum Theil neuer und sinnreicher Beobachtungen mit, aus welchen er den Schluſs zieht, daſs die seit Newton allgemein angenommene Theorie der Farbenmischung in den wesentlichsten Punkten irrig sey, und es namentlich nur zwei prismatische Farben gebe, nämlich Gelb und Indigo, welche vermischt Weiſs liefern. Daher mochte es nicht Überflüssig sein, zu zeigen, wie die Newton'sche Theorie der Farbenmischung bis zu einem gewissen Punkte hin, und namentlich der Satz, daſs jede Farbe ihre Complementarfarbe hat, welche mit ihr vermischt Weiſs liefert, aus unbestreitbaren Thatsachen mit mathematischer Evidenz hervorgeht, so daſs dieser Satz als einer der wohlbegründetsten in der Physik angesehen werden muſs. Ich werde dann zeigen wie die von Helmholtz angestellten positiven Beobachtungen, statt gegen diese Theorie zu zeugen, vielmehr dazu dienen können, dieselbe theils zu bestätigen, theils zu ergänzen.“

Seinen „Gesetzen der Farbmischung“ gibt er den folgenden Wortlaut:

1. (…) „jeder Farbeneindruck [zerlegt] (…) sich in drei mathematisch bestimmbare Momente (…) : den Farbenton, die Intensität der Farbe, und die Intensität des beigemischten Weiſs.“
2. (…) „wenn man von den beiden zu vermischenden Lichtern das eine stetig ändert (…), auch der Eindruck der Mischung sich stetig ändert.“
3. Es geben „ (…) zwei Farben, deren jede constanten Farbenton, constante Farbenintensität und constante Intensität des beigemischten Weiſs hat, auch constante Farbenmischung (…), gleich viel aus welchen homogenen Farben jene zusammengesetzt seien.“
4. (…) „die gesammte Lichtintensität der Mischung [ist] die Summe (…) aus den Intensitäten der gemischten Lichter.“

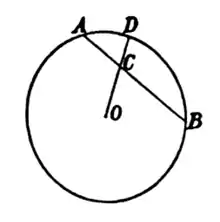
Zur Veranschaulichung fügte er verschiedene grafische Darstellungen bei, wie es die nebenstehende Abbildung beispielhaft zeigt. Mit dieser geometrischen Darstellung der Beziehungen auf der Farbebene beschreibt er eine bestimmte Mischung aus Anteilen der Farben A und B mithilfe der folgenden Definitionen und Termen:

A und B sind homogene Farben, O ist der Weißpunkt;

D stellt die die maximale Sättigung dar und der Farbpunkt C entspricht dem Farbton in seinem Schweregrad.

(a+b)OC steht für die Intensität der Farbanteile.
(a+b)CD stellt die Intensität des Weißanteils dar.
(a+b)OD (mit OD = 1) drückt die Totalintensität aus.

Dies zeigt den „rein mathematischen“ Ansatz, der seinem Gedanken zugrunde liegt. Graßmann kam zu dem Schluss, dass er mit seinen vier Gesetzen, die allesamt auf Erfahrung beruhten, eine Art der Darstellung geschaffen hatte, welche die bis dato benutzte „empirische Regel“ Newtons ersetzen konnte.[2]

Die von Graßmann aufgestellten Gesetze wurden lange Jahre in der wissenschaftlichen Welt so gut wie nicht anerkannt – heute jedoch bilden sie eine weitestgehend immer noch gültige Grundlage aller modernen Farblehren und -räume.

Erstes graßmannsches Gesetz

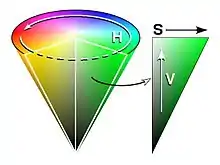
Jeder Farbeindruck kann mit genau drei Grundgrößen vollständig beschrieben werden.

Mathematische Notation:

\{C\}\equiv R.\{R\}+G.\{G\}+B.\{B\}

bzw.

\{C\}\equiv {\begin{pmatrix}R\\G\\B\end{pmatrix}}

in alternativer Schreibung.

Graßmann selbst benutzte dabei gerne die drei Grundgrößen Grundfarbe (Spektralfarbe), Farbintensität und Weißintensität. Heute wird diese Dreiheit als HSV-Farbraum bezeichnet und ist im nebenstehenden Bild modellhaft als Kegel dargestellt; die Kürzel stehen für Hue (Farbton), Saturation (Sättigung) und Value of Lightness (auch Brightness oder Luminance, deutsch Dunkelstufe). Das Gesetz ist aber auch auf drei Primärfarben (etwa die CIE-Primärvalenzen oder RGB) anwendbar – eben drei Farben, die jeweils nicht durch eine Mischung der beiden übrigen hergestellt werden können.

Zweites graßmannsches Gesetz

Mischt man eine Farbe mit sich veränderndem Farbton mit einer Farbe, bei der der Farbton immer gleich bleibt, so entstehen Farben mit sich veränderndem Farbton, wie es durch die Schnittmengen der Farbflächen im Begleitbild illustriert wird.

Mathematische Notation:

Zwei Farben,

\{C_{1}\}\equiv {\begin{pmatrix}R_{1}\\G_{1}\\B_{1}\end{pmatrix}}

und

\{C_{2}\}\equiv {\begin{pmatrix}R_{2}\\G_{2}\\B_{2}\end{pmatrix}}

ergeben nach additiver Farbmischung die Farbe

\{C\}\equiv \{C_{1}\}+\{C_{2}\}\equiv {\begin{pmatrix}R_{1}+R_{2}\\G_{1}+G_{2}\\B_{1}+B_{2}\end{pmatrix}}

Hiermit beschreibt Graßmann im Prinzip die (mathematische) Homogenität des Farbraumes – egal welche Farbtonveränderung man an einer Farbe vornimmt, das Mischprodukt folgt analog.

Drittes graßmannsches Gesetz

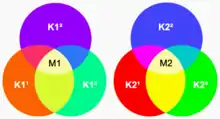
Der Farbton einer durch additive Farbmischung entstandenen Farbe hängt nur vom Farbeindruck der Ausgangsfarben, nicht jedoch von deren physikalischen (spektralen) Zusammensetzungen ab. Das Bild rechts demonstriert die Entstehung zweier zueinander metamerer Farben (M1 und M2) aus unterschiedlichen Farbkomponenten (K1¹, K1² und K1³ bzw. K2¹, K2² und K2³).

Mathematische Notation:

\{C'\}\equiv k.\{C\}\equiv {\begin{pmatrix}k.R\\k.G\\k.B\end{pmatrix}}

Dieses Gesetz besagt, dass das Mischverhalten selbst der metameren Farben – also derjenigen Farben mit gleichem Farbeindruck, aber zugleich unterschiedlicher spektraler Zusammensetzung – rein aufgrund ihres Farbeindruckes exakt beschrieben werden kann. Umgekehrt können also vom Mischverhalten her keine unmittelbaren Rückschlüsse auf die spektrale Zusammensetzung einer Farbe gezogen werden.

Viertes graßmannsches Gesetz

Die Intensität (bzw. Totalintensität) einer additiv gemischten Farbe (T3) entspricht der Summe der Intensitäten der Ausgangsfarben
(im Schema beschränkt auf T1 und T2).

Mathematische Notation:

T(A+B)\equiv T(A)+T(B)

(mit T als Entsprechung der Totalintensität bzw. Luminanz eines Farbeindrucks)

Laut David L. MacAdam gilt dieses Gesetz nur für den Spezialfall einer idealisierten, auf einen Punkt reduzierten Quelle, nicht aber für ausgedehntere Farbflächen. Graßmann hatte sich nur mit dem oben genannten Spezialfall befasst.

Einzelnachweise

Günther Wyszecki, W. S. Stiles, „Color Science: Concepts and Methods, Quantitative Data and Formulae“, ISBN 978-0-471-39918-6
H. Grassmann, „Zur Theorie der Farbenmischung“, Poggendorffs Annalen 69, 1853, S. 69–84. Google Books. Abgerufen am 1. Februar 2017.

Siehe auch

Weblinks

Das Grassmann'sche Experiment (PDF; 7 MB)
Seminararbeit Daniel Göhring: Hermann Günter Grassmann - Leben und die Grassmannschen Gesetze (PDF; 645 kB)
Anna Katharina Hirschmüller, „Untersuchungen zur Wahrnehmung von Oberflächen- und Beleuchtungsfarben“, (Dissertationsarbeit, PDF; 6 MB)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Günther Wyszecki, W. S. Stiles, „Color Science: Concepts and Methods, Quantitative Data and Formulae“, ISBN 978-0-471-39918-6

[2] H. Grassmann, „Zur Theorie der Farbenmischung“, Poggendorffs Annalen 69, 1853, S. 69–84. Google Books. Abgerufen am 1. Februar 2017.