Optimalfarbe
Eine Optimalfarbe ist eine idealisierte Körperfarbe mit rechteckigem Spektrum.
Geschichte
Die Optimalfarbe geht auf einen Vorschlag von Wilhelm Ostwald zurück. Anfang des 20. Jahrhunderts war die Suche nach einem rechnerisch beherrschbaren System für Farben durch Forderungen der Industrie und die Möglichkeiten der Messung von Spektren entstanden. Der Physiker Erwin Schrödinger konnte 1919 in seiner Arbeit Theorie der Pigmente von größter Leuchtkraft[1] den Beweis erbringen, dass Optimalfarben die theoretische Grenze aller realisierbaren Körperfarben sind.
Aufbau
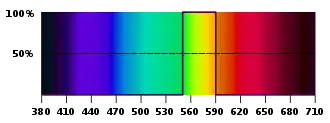
Die Idealisierung einer Optimalfarbe besteht darin, dass für ihr Spektrum maximal zwei Sprungstellen zugelassen werden. Ansonsten hat die Intensität, der Remissionsgrad β, nur den Wert 0 oder 1.
Hat das Spektrum nur eine Sprungstelle, so werden je nach ihrer Lage unterschieden (Beschreibung jeweils in Richtung wachsender Wellenlängen):
- Kurzendfarben; blaue Farben, die bei niedrigen Wellenlängen (am „kurzen Ende des Spektrums“) mit β = 1 beginnen und dann bei einer definierten Wellenlänge auf β = 0 sinken
- Langendfarben; rote Farben, bei denen der Remissionsgrad auf 1 springt und diesen Wert bis zum („langen“) Ende des sichtbaren Spektralbereichs behält.
Hat das Spektrum zwei Sprungstellen, so handelt es sich um:
- grüne Mittelfarben, deren voller Bereich (β = 1) in der Mitte liegt.
- Mittelfehlfarben, wenn die Kurve in der Mitte den Wert β = 0 hat; sie gehören im Prinzip zur Gruppe der Violett-(Purpur-)töne.
Eigenschaften
Eine Optimalfarbe hat von allen Farben gleicher Farbart die größte Helligkeit und von allen Farben gleichen Farbtons und gleicher Helligkeit die höchste Sättigung.
David L. MacAdam und Siegfried Rösch haben das Konzept später erweitert, um Aussagen über die Gesamtheit der theoretisch realisierbaren Körperfarben (etwa für Mal- und Anstrichfarben) treffen zu können. Die unendliche Menge der Optimalfarben bildet den Optimalfarbkörper, der innerhalb eines Farbraumes die Menge aller theoretisch realisierbaren Körperfarben wiedergibt. Alle realen Farben, also Farben mit nicht-optimalen Spektren, bilden einen Unterraum des Optimalfarbkörpers, liegen also innerhalb dessen Grenzen.
Das bekannteste Beispiel für einen Optimalfarbkörper dürfte der „Farbenberg von Rösch“ sein. Der Psychophysiker Douglas MacAdam hat diesen Farbkörper und seine exakte Grenzen als erster berechnet, weshalb der Farbkörper auch MacAdam limits (deutsch: MacAdam-Grenzen) genannt wird. Die MacAdam limits bilden den Optimalfarbkörper im CIExyY-Farbraum ab. Die genaue Form bzw. Größe dieses Farbkörpers hängt von der Leuchtdichte ab und beinhaltet alle Farben, die durch Streuung, Reflexion und Lichtbrechung zustande kommen können.
Eine entscheidende Eigenschaft des Optimalfarbkörpers ist, dass es zu jedem Punkt (jeder Farbe) auf der Oberfläche dieses Körpers nur ein einziges Reizspektrum gibt. Das bedeutet, dass zu allen Farben auf der Optimalfarbkörper-Oberfläche keine Metamere existieren. Innerhalb des Körpers dagegen gibt es zu jeder Farbe unendlich viele Metamere; je weiter innen die Farbe im Optimalfarbkörper liegt, desto größer ist Häufigkeitsdichte ihrer Metamere.
Für das Ostwald-System sind die Optimalfarben grundlegend. Als Vollfarbe sind sie die volle bunte Komponente, gekennzeichnet mit der Farbtonkennzahl N. Um die zu kennzeichnende Farbe zu erreichen, wird eine additive Mischung mit „reinem“ Weißanteil w und „reinem“ Schwarzanteil s durchgeführt. Die Abstufung erfolgt im Sinne des Weber-Fechner-Gesetzes.
Ostwalds Farbsystem wurde zu seinen Lebzeiten vor allem von Physikern wie etwa Kohlrausch kritisiert, was besonders in dessen „Bemerkungen zur sogenannten Ostwald’schen Farbentheorie“ zum Ausdruck kommt.
Literatur
- Wilhelm Ostwald: Physikalische Farbenlehre. Band 2, 2. Auflage. Leipzig 1923.
Weblinks
Einzelnachweise
- Erwin Schrödinger: Theorie der Pigmente von größter Leuchtkraft. Annalen der Physik, Band 367, Ausgabe 15, pp. 603–622