Betragsoptimum

Beim Betragsoptimum handelt es sich um einen Begriff aus der Regelungstheorie, genauer um ein regelungstechnisches Optimierungskriterium im Frequenzraum.[1] Eine Regelung wird allgemein dann als optimal bezeichnet, wenn die Regelgröße dem Wert der Führungsgröße mit möglichst geringer zeitlicher Verzögerung folgen kann. Bei der Optimierung mittels des Betragsoptimums wird die Einschwingzeit eines Regelsystems optimiert.[2]

Ein weiteres Optimierungskriterium im Frequenzbereich ist das symmetrische Optimum.

Motivation

Die möglichen Verläufe des Amplitudenganges eines geschlossenen Regelkreises beim Führungsverhalten. Die Kenngrößen sind:

\omega _{R}

– Resonanzfrequenz,

\omega _{d}

– Durchtrittsfrequenz,

\omega _{B}

– Bandbreite, M_max – Betrag des Frequenzgangs an der Resonanzstelle.

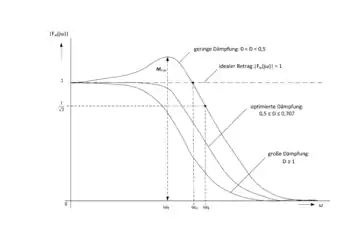
Eine kurze Anstiegszeit bzw. Anregelzeit wie bei der Sprungantwort bedingt eine große Bandbreite des geschlossenen Regelkreises. Es ist ein direkter Bezug zwischen der Anstiegszeit T_An und der Bandbreite $\omega _{B}$ der Führungsübergangsfunktion gegeben. Mathematisch gesehen ist der Bezug wie folgt:[3]

T_{\text{An}}={\frac {\pi }{\omega _{B}}}={\frac {\pi }{2\pi \cdot f_{B}}}={\frac {1}{2\cdot f_{B}}}

Für gutes Führungsverhalten wird beim Betragsoptimum das Verhältnis der Ausgangs- zur Eingangsamplitude (Amplituden-Frequenzgang) optimiert. Im Idealfall ist der Betrag des Frequenzganges F für alle Kreisfrequenzen ω:[4]

|F_{w}(\mathrm {j} \omega )|=1

.

Es wird auch von einer Betragsanschmiegung von F_w(jω) an Eins gesprochen.[3] In realen Regelkreisen treten allerdings immer Verzögerungen auf, weshalb dieses ideale Betragsoptimum nur in Näherung erreicht werden kann und es bei höheren Frequenzen zu einer Verkleinerung des Amplituden-Frequenzganges kommt. Das Optimierungsverfahren des Betragsoptimums versucht über einen möglichst großen Frequenzbereich von ω den Betrag des Frequenzgangs auf oder Nahe dem Wert 1 zu halten, dazu werden die Parameter des Reglers aus den Zeitkonstanten der Regelstrecke berechnet.[5]

Voraussetzungen zur Anwendung des Betragsoptimums

Blockschaltbild eines einfachen Standardregelkreises, bestehend aus der Regelstrecke, dem Regler und einer negativen Rückkopplung der Regelgröße y (auch Istwert). Die Regelgröße y wird mit der Führungsgröße (Sollwert) w verglichen. Die Regelabweichung e = w – y wird dem Regler zugeführt, der daraus entsprechend der gewünschten Dynamik des Regelkreises eine Stellgröße u bildet. Die Stabilität des Systems hängt unter anderem von den Streckenpolen ab. Die Erklärung wird nebenstehend aufgeführt.

Zur Anwendung des Betragsoptimum werden gewisse Voraussetzungen gestellt, diese gilt es einzuhalten. Werden die Voraussetzungen nicht eingehalten kann es zu undefinierten Zuständen kommen. Zum Beispiel könnte die Stellgrößenbegrenzung überschritten werden. Eine Folge könnte sein, dass das System eine unerwartete Reaktion herbeiführt, wie die Zerstörung elektrischer Bestandteile. So wird davon ausgegangen, dass bei dem Reglerentwurf die Messeinrichtung zu der Regelstrecke gezählt wird und somit ein Standardregelkreis vorliegt. Die Parameter der Regelstrecke, Zeitkonstanten und Verstärkungsfaktor, müssen bereits bekannt sein.[6] Des Weiteren wird bei der Herleitung, als auch bei den Einstellregeln für das Betragsoptimum, davon ausgegangen, dass es sich bei der Regelstrecke um eine Zusammensetzung aus Verzögerungssystemen handelt. Bei nichtreellen Streckenpolen besteht die Gefahr von Stabilitätsschwierigkeiten. Wenn konjugiert komplexe Pole in der Regelstrecke vorhanden sind, sollten diese hinreichend gedämpft sein. Jedoch wäre die Verwendung von rein reellen Polen vorzuziehen.[5] Eine nicht schwingfähige Regelungsstrecke mit Ausgleich ist somit vorauszusetzen. Bei Verwendung von dominanten Zeitkonstanten, d. h. eine oder zwei große Zeitkonstanten gegenüber der Ersatzzeitkonstante T_E, sind besonders brauchbare Resultate zu erwarten. Werden die Voraussetzungen eingehalten so ist ein gutes Führungsverhalten garantiert.[7]

Mathematischer Hintergrund

Das Verfahren wurde für einen Regelkreis II. Ordnung abgeleitet. Zudem wird bei der Herleitung in zwei Typen unterschieden: Anwendung des Betragsoptimums für Regelstrecken I. Ordnung und Anwendung des Betragsoptimums für Regelstrecken höherer Ordnung. Es existieren Hilfssätze um die Regelstrecke zu vereinfachen, diese werden angewendet bei Strecken höherer Ordnung und Totzeitelementen.[2]

Satz von der Summe aller kleinen Zeitkonstanten

Liegt eine Regelstrecke höherer Ordnung vor, welche folgende Form aufweist: $G_{s}(s)={\frac {K_{S}}{(1+T_{1}\cdot s)\cdot (1+T_{2}\cdot s)...(1+T_{n}\cdot s)}}$ ,
so kann eine Ersatzzeitkonstante T_E, welche sich aus der Summe aller kleinen Zeitkonstanten zusammensetzt, gebildet werden. Hierbei wird unterschieden, ob es eine oder zwei dominante Zeitkonstanten gibt. Dies wird auch als Satz von der Summe aller kleinen Zeitkonstanten bezeichnet.[2]

Im Fall einer dominanten Zeitkonstante gilt[5]: $\quad \quad \quad T_{E}=\sum _{i=2}^{n}T_{i},\quad T_{1}\gg T_{E},\quad G_{s}(s)={\frac {K_{S}}{(1+T_{1}\cdot s)\cdot (1+T_{E}\cdot s)}}$

Im Fall von zwei dominanten Zeitkonstanten gilt[7]: $\quad T_{E}=\sum _{i=3}^{n}T_{i},\quad T_{1}>T_{2}\gg T_{E},\quad G_{s}(s)={\frac {K_{S}}{(1+T_{1}\cdot s)\cdot (1+T_{2}\cdot s)\cdot (1+T_{E}\cdot s)}}$

Vereinfachung von Totzeitelementen

Sei eine Totzeit T_t deutlich kleiner als die Zeitkonstante T₁ eines Verzögerungssystems, das gleiche wäre gültig bei einem I-Glied und dessen Integrationszeit T_I, so kann diese als PT₁-Glied ersetzt werden. Bei dieser Überlegung wird von dem offenen Regelkreis G₀(s) ausgegangen. "Dabei wird die Reihenentwicklung der Exponential-Funktion für das Totzeitelement nach dem ersten Glied abgebrochen:"[2]

$G_{0}(s)={\frac {K_{R}\cdot K_{S}\cdot e^{-T_{t}\cdot s}}{1+T_{1}\cdot s}}={\frac {K_{R}\cdot K_{S}}{(1+T_{1}\cdot s)\cdot (1+{\frac {T_{t}\cdot s}{1!}}+{\frac {(T_{t}\cdot s)^{2}}{2!}}+...)}}={\frac {K_{R}\cdot K_{S}}{(1+T_{1}\cdot s)\cdot (1+T_{t}\cdot s)}}$ , wenn $T_{1}\gg T_{t}$ gilt.

Anwendung des Betragsoptimums für Regelstrecken Ι. Ordnung

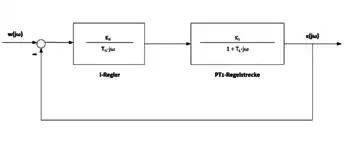
Dargestellt ist ein Regelkreis II. Ordnung mit einem I-Regler und einer PT₁-Regelstrecke. Aufgeschaltet wird das Eingangssignal w(j $\omega$ ) und abgerufen am Ausgang das Ausgangssignal x(j $\omega$ ).

Nachfolgend wird die Herleitung für die Anwendung des Betragsoptimums für Regelstrecken I. Ordnung beschrieben, diese baut auf dem Sachverhalt des Abschnittes Motivation auf. Ein Regelkreis II. Ordnung, zusammengesetzt aus einem I-Regler und einer PT₁-Regelstrecke, besitzt folgende Frequenzgangfunktion als offener Regelkreis:[2]

$F_{\text{RS}}(j\omega )={\frac {K_{S}}{T_{I}\cdot j\omega \cdot (1+T_{E}\cdot j\omega )}}$ , mit ${\frac {1}{T_{I}}}={\frac {K_{R}}{T_{N}}}$ .

Nun wird mittels des offenen Regelkreises der geschlossene Regelkreis gebildet, der folgende Frequenzgangfunktion aufweist:

$F(j\omega )={\frac {F_{\text{RS}}(j\omega )}{1+F_{\text{RS}}(j\omega )}}={\frac {K_{S}}{T_{I}\cdot j\omega \cdot (1+T_{E}\cdot j\omega )+K_{S}}}={\frac {K_{S}}{K_{S}-T_{I}\cdot T_{E}\cdot \omega ^{2}+T_{I}\cdot j\omega }}$

Da der Betrag für einen möglichst großen Bereich gleich 1 sein soll, gilt (es wird das Betragsquadrat verwendet, um die Wurzel im Nenner zu beseitigen):

$|F(j\omega )|={\frac {K_{S}}{\sqrt {(K_{S}-T_{I}\cdot T_{E}\cdot \omega ^{2})^{2}+T_{I}^{2}\cdot \omega ^{2}}}}{\stackrel {\mathrm {!} }{\approx }}1$

$|F(j\omega )|^{2}={\frac {K_{S}^{2}}{(K_{S}-T_{I}\cdot T_{E}\cdot \omega ^{2})^{2}+T_{I}^{2}\cdot \omega ^{2}}}={\frac {K_{S}^{2}}{K_{S}^{2}+(T_{I}^{2}-2\cdot K_{S}\cdot T_{I}\cdot T_{E})\cdot \omega ^{2}+T_{I}^{2}\cdot T_{E}^{2}\cdot \omega ^{4}}}{\stackrel {\mathrm {!} }{\approx }}1$

Damit die Approximation für einen großen Bereich gültig ist, müssen möglichst viele Koeffizienten des Zähler- und Nennerpolynoms gleich sein. Somit folgt diese Gleichung:

$|F(j\omega )|^{2}={\frac {\quad K_{S}^{2}+\quad \quad \quad \quad \quad \quad \quad \quad \quad 0\cdot \omega ^{2}+\quad \quad \quad 0\cdot \omega ^{4}}{K_{S}^{2}+(T_{I}^{2}-2\cdot K_{S}\cdot T_{I}\cdot T_{E})\cdot \omega ^{2}+T_{I}^{2}\cdot T_{E}^{2}\cdot \omega ^{4}}}{\stackrel {\mathrm {!} }{\approx }}1$

Aus der Gleichung kann eine Realisierungstabelle für den Koeffizientenvergleich abgeleitet werden:

Zählerpolynom	Nennerpolynom	Realisierung
$K_{S}^{2}\cdot \omega ^{0}$	$K_{S}^{2}\cdot \omega ^{0}$	ist erfüllt
$0\cdot \omega ^{2}$	$(T_{I}^{2}-2\cdot K_{S}\cdot T_{I}\cdot T_{E})\cdot \omega ^{2}$	realisierbar
$0\cdot \omega ^{4}$	$T_{I}^{2}\cdot T_{E}^{2}\cdot \omega ^{4}$	nicht realisierbar

Somit ergibt sich folgende Optimierungsgleichung:

$(T_{I}^{2}-2\cdot K_{S}\cdot T_{I}\cdot T_{E})\cdot \omega ^{2}=0$

$T_{I}=2\cdot K_{S}\cdot T_{E}$ , es gilt $K_{I}={\frac {1}{T_{I}}}={\frac {1}{2\cdot K_{S}\cdot T_{E}}}$ .

Setzt man nun die Integrierkonstante T_I in die Frequenzgangfunktion des geschlossenen Regelkreises ein, so ergibt sich:

$F(j\omega )={\frac {K_{S}}{K_{S}+T_{I}\cdot j\omega +T_{I}\cdot T_{E}\cdot (j\omega )^{2}}}={\frac {K_{S}}{K_{S}+2\cdot K_{S}\cdot T_{E}\cdot j\omega +2\cdot K_{S}\cdot T_{E}^{2}\cdot (j\omega )^{2}}}={\frac {1}{1+2\cdot T_{E}\cdot j\omega +2\cdot T_{E}^{2}\cdot (j\omega )^{2}}}$

Geht man nun in den Laplace-Bereich und stellt die Übertragungsfunktion des geschlossenen Regelkreises G(s) auf, kann man diese mit einem standardisierten PT₂-Glied abgleichen.

$G(s)={\frac {1}{1+2\cdot T_{E}\cdot s+2\cdot T_{E}^{2}\cdot s^{2}}}{\stackrel {\mathrm {!} }{=}}{\frac {1}{1+2\cdot D\cdot T_{0}\cdot s+T_{0}^{2}\cdot s^{2}}}$

Durch einen Koeffizientenvergleich lassen sich die Dämpfung D und die Kennkreisfrequenz $\omega _{0}$ ermitteln.

$2\cdot T_{E}=2\cdot D\cdot T_{0},\quad 2\cdot T_{E}^{2}=T_{0}^{2}$ , es gilt $\omega _{0}={\frac {1}{T_{0}}}$ .

$T_{0}={\sqrt {2}}\cdot T_{E},\quad \omega _{0}={\frac {1}{{\sqrt {2}}\cdot T_{E}}}$

$D={\frac {T_{E}}{T_{0}}}={\frac {1}{\sqrt {2}}}$ , somit gilt eine feste Dämpfung für alle Frequenzen.

Anwendung des Betragsoptimums für Regelstrecken höherer Ordnung

Die Herleitung zur Anwendung des Betragsoptimums für Regelstrecken höherer Ordnung baut zum einen auf den Sachverhalt des Abschnittes Motivation, als auf die ermittelte optimale Einstellung für T_I aus dem Abschnitt Anwendung des Betragsoptimums für Regelstrecken Ι.Ordnung auf. Darüber hinaus wird die Herleitung unterteilt in die Kompensation einer großen Zeitkonstante und in die Kompensation von zwei großen Zeitkonstanten.

Kompensation einer großen Zeitkonstante

Ist eine Zeitkonstante der Regelstrecke deutlich größer als die Anderen, so kann die Nachstellzeit T_N eines PI-Reglers genutzt werden um die große Zeitkonstante T₁ zu kompensieren. Vorteil dieser Kompensation ist, dass die Schnelligkeit der Regelung verbessert und die mathematische Rechnung vereinfacht wird. Die mathematische Rechnung wird deshalb vereinfacht, da die Kompensation einer Kürzung gleicht. Mit dem Satz von der Summe aller kleinen Zeitkonstanten werden die kleinen Zeitkonstanten der Regelstrecke zur Ersatzzeitkonstante T_E zusammengefasst.[2]

Vorausgesetzt wird ein PI-Regler und eine PT₂-Strecke bzw. PT_n-Strecke. Bei einer PT₂-Strecke bildet sich folgende Übertragungsfunktion für den offenen Regelkreis:

$G_{\text{RS}}(s)=G_{R}(s)\cdot G_{S}(s)={\frac {K_{R}\cdot (1+T_{N}\cdot s)}{T_{N}\cdot s}}\cdot {\frac {K_{S}}{(1+T_{1}\cdot s)\cdot (1+T_{E}\cdot s)}}$ , es gilt $T_{1}\gg T_{E}$ .

Wenn die Nachstellzeit T_N nun gleich der großen Verzögerungszeitkonstante T₁ gewählt wird ergibt sich eine Kürzung. Somit entsteht die Optimierungsvorschrift $T_{N}=T_{1}$ .

$G_{\text{RS}}(s)=G_{R}(s)\cdot G_{S}(s)={\frac {K_{R}}{T_{N}\cdot s}}\cdot {\frac {K_{S}}{(1+T_{E}\cdot s)}}$

Auf Grundlage des Abschnittes Anwendung des Betragsoptimums für Regelstrecken Ι.Ordnung folgt unter Verwendung der optimalen Einstellung für T_I die Optimierungsvorschrift für K_R.

$T_{I}=2\cdot K_{S}\cdot T_{E}={\frac {T_{N}}{K_{R}}},\quad K_{R}={\frac {T_{N}}{2\cdot K_{S}\cdot T_{E}}}$

Kompensation von zwei großen Zeitkonstanten

Für die Kompensation von zwei großen Zeitkonstanten werden die kleinen Zeitkonstanten wie schon im Abschnitt Anwendung des Betragsoptimums für Regelstrecken höherer Ordnung zu der Ersatzzeitkonstante T_E zusammengefasst. Des Weiteren wird ein PID-Regler eingesetzt, um mit Hilfe der Nachstellzeit T_N und der Vorhaltzeit T_V des Reglers die zwei großen Zeitkonstanten der Regelstrecke zu kompensieren. Vorteil dieser Kompensation ist, dass die Schnelligkeit der Regelung verbessert und die mathematische Rechnung vereinfacht wird. Die mathematische Rechnung wird deshalb vereinfacht, da die Kompensation einer Kürzung gleicht.[2]

Es ergibt sich folgende Übertragungsfunktion für den offenen Regelkreis, beim Einsatz eines PID-Reglers und einer PT₃-Regelstrecke:

$G_{\text{RS}}(s)=G_{R}(s)\cdot G_{S}(s)={\frac {K_{R}\cdot (1+T_{N}\cdot s)\cdot (1+T_{V}\cdot s)}{T_{N}\cdot s}}\cdot {\frac {K_{S}}{(1+T_{1}\cdot s)\cdot (1+T_{2}\cdot s)\cdot (1+T_{E}\cdot s)}}$ , es gilt $T_{1}>T_{2}\gg T_{E}$ .

Bei der Kompensation von zwei großen Zeitkonstanten ergibt sich die nachfolgende Reglereinstellung:

$T_{N}=T_{1},\quad T_{V}=T_{2},\quad$ für $T_{1}>T_{2}$ .

Nach der Kompensation ergibt sich dieselbe Übertragungsfunktion wie schon im Abschnitt Anwendung des Betragsoptimums für Regelstrecken höherer Ordnung:

$G_{\text{RS}}(s)=G_{R}(s)\cdot G_{S}(s)={\frac {K_{R}}{T_{N}\cdot s}}\cdot {\frac {K_{S}}{(1+T_{E}\cdot s)}}$

Die Optimierungsvorschrift für den Reglerverstärkungsfaktor K_R ist somit dieselbe wie bei dem Einsatz eines PI-Reglers und einer PT₂-Strecke:

$K_{R}={\frac {T_{N}}{2\cdot K_{S}\cdot T_{E}}}$

Einstellregeln für das Betragsoptimum

In der nachfolgenden Tabelle sind die Strecken- und Reglerstrukturen, inklusive der Angabe des Übertragungsverhaltens, dargestellt. Zudem sind die jeweiligen Einstellregeln für das Betragsoptimum hinzugefügt. Die Einstellregeln gelten nur, wenn die Voraussetzungen erfüllt sind.[2]

Regelstrecke		Regler
Typ	Übertragungsfunktion	Typ	Übertragungsfunktion
PT₁	$G_{S}(s)={\frac {K_{S}}{1+T_{1}\cdot s}}$ $T_{E}=T_{1}$	I	$G_{R}(s)={\frac {K_{I}}{s}},\quad G_{R}(s)={\frac {1}{T_{I}\cdot s}}$ $K_{I}={\frac {1}{2\cdot K_{S}\cdot T_{E}}},\quad T_{I}=2\cdot K_{S}\cdot T_{E}$
PT₂	$G_{S}(s)={\frac {K_{S}}{(1+T_{1}\cdot s)\cdot (1+T_{2}\cdot s)}}$ $T_{1}>T_{2},\quad T_{E}=T_{2}$	PI	$G_{R}(s)={\frac {K_{R}\cdot (1+T_{N}\cdot s)}{T_{N}\cdot s}}$ $T_{N}=T_{1},\quad K_{R}={\frac {T_{N}}{2\cdot K_{S}\cdot T_{E}}}$
PT_n	$G_{S}(s)={\frac {K_{S}}{(1+T_{1}\cdot s)\cdot (1+T_{E}\cdot s)}}$ $T_{1}\gg T_{E},\quad T_{E}=\sum _{i=2}^{n}T_{i}$	PI	$G_{R}(s)={\frac {K_{R}\cdot (1+T_{N}\cdot s)}{T_{N}\cdot s}}$ $T_{N}=T_{1},\quad K_{R}={\frac {T_{N}}{2\cdot K_{S}\cdot T_{E}}}$
PT_n	$G_{S}(s)={\frac {K_{S}}{(1+T_{1}\cdot s)\cdot (1+T_{2}\cdot s)\cdot (1+T_{E}\cdot s)}}$ $T_{1}>T_{2}\gg T_{E},\quad T_{E}=\sum _{i=3}^{n}T_{i}$	PID	$G_{R}(s)={\frac {K_{R}\cdot (1+T_{N}\cdot s)\cdot (1+T_{V}\cdot s)}{T_{N}\cdot s}}$ $T_{N}=T_{1},\quad T_{V}=T_{2},\quad K_{R}={\frac {T_{N}}{2\cdot K_{S}\cdot T_{E}}}$

Betragsoptimum im Vergleich

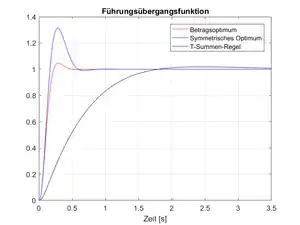
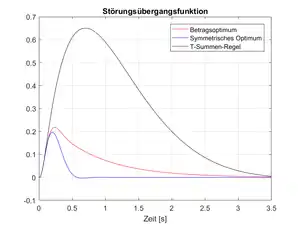
Vergleich des Betragsoptimums mit einer empirischen Einstellregel, T-Summen-Regel, und einem weiteren Optimierungskriterium aus dem Frequenzbereich, Symmetrisches Optimum. Abbildung der Führungsübergangsfunktion für einen Sollsprung w₀ = 1.

Vergleich des Betragsoptimums mit einer empirischen Einstellregel, T-Summen-Regel, und einem weiteren Optimierungskriterium aus dem Frequenzbereich, Symmetrisches Optimum. Abbildung der Störungsübergangsfunktion für einen Sollsprung z₀ = 1 am Streckeneingang.

Um die Stärken des Betragsoptimums zu verdeutlichen, wird nachfolgend ein Vergleich mit mehreren Verfahren vorgeführt. Dabei steht die Regelung einer PT₃-Strecke mit einem PI-Regler im Fokus. Zum Vergleich wird eine empirische Einstellregel aus dem Zeitbereich, sowie ein weiteres Optimierungskriterium aus dem Frequenzbereich herangezogen. Aus dem Spektrum der empirischen Einstellregeln wird die schnelle Regelung nach der T-Summen-Regel genommen. Aus den Optimierungskriterien im Frequenzbereich wird das Symmetrische Optimum gewählt.[3][4][6][8]

Gegeben sei folgende Regelstrecke: $G_{S}(s)={\frac {K_{S}}{(1+T_{1}\cdot s)\cdot (1+T_{2}\cdot s)\cdot (1+T_{3}\cdot s)}}$

mit den Streckenparametern: $K_{S}=1{,}78,\quad T_{1}=0{,}73,\quad T_{2}=0{,}031,\quad T_{3}=0{,}021$

Der PI-Regler soll wie folgt aussehen: $G_{R}(s)={\frac {K_{R}\cdot (1+T_{N}\cdot s)}{T_{N}\cdot s}}$

Einstellung der Regelparameter nach dem Betragsoptimum (s. Tabelle, 3 Zeile):
$T_{N}=T_{1}=0{,}73$
$T_{E}=T_{2}+T_{3}=0{,}052$ , da $T_{N}\gg T_{E}$ gültig ist.
$K_{R}={\frac {T_{N}}{2\cdot K_{S}\cdot T_{E}}}=3{,}9434$
$G_{R}(s)={\frac {K_{R}\cdot (1+T_{N}\cdot s)}{T_{N}\cdot s}}={\frac {3{,}94\cdot (1+0{,}73\cdot s)}{0{,}73\cdot s}}$

Einstellung der Regelparameter nach dem Symmetrischen Optimum (es sei $a=2$ ):
IT₁-Näherung: $G_{S}(s)={\frac {K_{S}}{s\cdot (1+T_{1}\cdot s)}}={\frac {1{,}78}{0{,}73\cdot s\cdot (1+0{,}052\cdot s)}}$
$T_{1}=0{,}052,\quad K_{S}={\frac {1{,}78}{0{,}73}}=2{,}44$
$T_{N}=a^{2}\cdot T_{1}=0{,}208$
$K_{R}={\frac {1}{a\cdot K_{S}\cdot T_{1}}}=3{,}9434$
$G_{R}(s)={\frac {K_{R}\cdot (1+T_{N}\cdot s)}{T_{N}\cdot s}}={\frac {3{,}94\cdot (1+0{,}21\cdot s)}{0{,}21\cdot s}}$

Einstellung der Regelparameter nach der T-Summen-Regel (schnelle Regelung):
$K_{S}=1{,}78,\quad T_{\sum }=T_{1}+T_{2}+T_{3}=0{,}782$
$T_{N}=0{,}7\cdot T_{\sum }=0{,}5474$
$K_{R}={\frac {1}{K_{S}}}=0{,}5618$
$G_{R}(s)={\frac {K_{R}\cdot (1+T_{N}\cdot s)}{T_{N}\cdot s}}={\frac {0{,}56\cdot (1+0{,}55\cdot s)}{0{,}55\cdot s}}$

Anhand der Führungsübergangsfunktion lässt sich erkennen, dass das Betragsoptimum eine deutlich geringere An- und Ausregelzeit aufweist gegenüber der empirischen Einstellregel. Dies ist auf den Größenunterschied des Regler-Verstärkungsfaktors K_R zurückzuführen, dieser ist bei der T-Summen-Regel deutlich kleiner. Des Weiteren ist der Überschwinger des Betragsoptimums wesentlich niedriger, als der des Symmetrischen Optimums. Der Grund ist die Nachstellzeit T_N, diese ist zwar geringer beim Symmetrischen Optimum und führt deshalb nochmal zu einer etwas besseren Anregelzeit. Der zu zahlende Preis ist jedoch ein größerer Überschwinger und eine erhöhte Ausregelzeit.

Anwendungsbereiche

Das Betragsoptimum ist wegen seiner Stärken in der Praxis unumstritten[9] und wird vorzugsweise im Bereich der elektrischen Regelung eingesetzt.[5] Darüber hinaus ist ein weiterer Einsatzschwerpunkt des Verfahrens der Einsatz in der Antriebstechnik.[6],[10]

Das Betragsoptimum wird häufig für die Einstellung von

Geschwindigkeits-,
Strom-,
Drehmoment- und
Kraftregelungen

eingesetzt. Dabei erstrecken sich die Einsatzgebiete von

Hauptantriebe von Werkzeugmaschinen,
Vorschubantriebe von Werkzeugmaschinen und Industrierobotern
bis hin zu Aufzügen.[2]

Siehe auch

Literatur

Slobodan N. Vukosavić: Digital Control of Electrical Drives. Springer-Verlag, New York 2007, ISBN 978-0-387-48598-0.
Dierk Schröder: Elektrische Antriebe – Regelung von Antriebssystemen. Springer-Verlag, Berlin, Heidelberg 2015, ISBN 978-3-642-30471-2.
Gert-Helge Geitner: Entwurf digitaler Regler für elektrische Antriebe. VDE-Verlag, Berlin, Offenbach 1996, ISBN 3-8007-1847-2.

Weblinks

BOD - Das Digitale Betragsoptimum

Einzelnachweise

Ekbert Hering, Heinrich Steinhart: Taschenbuch der Mechatronik. Hanser Verlag, Leipzig 2005, ISBN 978-3-446-22881-8, S. 100.
Holger Lutz, Wolfgang Wendt: Taschenbuch der Regelungstechnik mit MATLAB und Simulink. 12. Auflage. Verlag Europa-Lehrmittel, Haan-Gruiten 2021, ISBN 978-3-8085-5870-6, S. 504–515.
Gerd Schulz: Regelungstechnik: Grundlagen, Analyse und Entwurf von Regelkreisen, rechnergestützte Methoden. Springer, Berlin 1995, ISBN 3-540-59326-8, S. 151–154.
Manfred Reuter, Serge Zacher: Regelungstechnik für Ingenieure: Analyse, Simulation und Entwurf von Regelkreisen. 10. Auflage. Vieweg, Braunschweig 2002, ISBN 3-528-94004-2, S. 236–237.
Otto Föllinger, Ulrich Konigorski (Bearb.): Regelungstechnik: Einführung in die Methoden und ihre Anwendung. 11. Auflage. VDE-Verlag, Berlin 2013, ISBN 978-3-8007-3231-9, S. 201–203.
Thomas Beier, Petra Wurl: Regelungstechnik: Basiswissen, Grundlagen, Beispiele. 2. Auflage. Fachbuchverlag Leipzig, München 2015, ISBN 978-3-446-44210-8, S. 177–185.
Jörg Kahlert: Crashkurs Regelungstechnik: Eine praxisorientierte Einführung mit Begleitsoftware. 2. Auflage. VDE-Verlag, Berlin 2015, ISBN 978-3-8007-3642-3, S. 150–153.
A. Weigl-Seitz: Regelungstechnik. Darmstadt 2015, S. 23–35.
Hans-Werner Philippsen: Einstieg in die Regelungstechnik: Vorgehensmodell für den praktischen Reglerentwurf. Fachbuchverlag Leipzig, München 2004, ISBN 3-446-22377-0, S. 141–143.
Rolf Schönfeld: Regelungen und Steuerungen in der Elektrotechnik. Verlag Technik, Berlin, München 1993, ISBN 3-341-01027-0, S. 78–96, 151–154.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Hering-1] Ekbert Hering, Heinrich Steinhart: Taschenbuch der Mechatronik. Hanser Verlag, Leipzig 2005, ISBN 978-3-446-22881-8, S. 100.

[Lutz-2] Holger Lutz, Wolfgang Wendt: Taschenbuch der Regelungstechnik mit MATLAB und Simulink. 12. Auflage. Verlag Europa-Lehrmittel, Haan-Gruiten 2021, ISBN 978-3-8085-5870-6, S. 504–515.

[Schulz-3] Gerd Schulz: Regelungstechnik: Grundlagen, Analyse und Entwurf von Regelkreisen, rechnergestützte Methoden. Springer, Berlin 1995, ISBN 3-540-59326-8, S. 151–154.

[Reuter-4] Manfred Reuter, Serge Zacher: Regelungstechnik für Ingenieure: Analyse, Simulation und Entwurf von Regelkreisen. 10. Auflage. Vieweg, Braunschweig 2002, ISBN 3-528-94004-2, S. 236–237.

[Föllinger-5] Otto Föllinger, Ulrich Konigorski (Bearb.): Regelungstechnik: Einführung in die Methoden und ihre Anwendung. 11. Auflage. VDE-Verlag, Berlin 2013, ISBN 978-3-8007-3231-9, S. 201–203.

[Beier-6] Thomas Beier, Petra Wurl: Regelungstechnik: Basiswissen, Grundlagen, Beispiele. 2. Auflage. Fachbuchverlag Leipzig, München 2015, ISBN 978-3-446-44210-8, S. 177–185.

[Kahlert-7] Jörg Kahlert: Crashkurs Regelungstechnik: Eine praxisorientierte Einführung mit Begleitsoftware. 2. Auflage. VDE-Verlag, Berlin 2015, ISBN 978-3-8007-3642-3, S. 150–153.

[Weigl-Seitz-8] A. Weigl-Seitz: Regelungstechnik. Darmstadt 2015, S. 23–35.

[Philippsen-9] Hans-Werner Philippsen: Einstieg in die Regelungstechnik: Vorgehensmodell für den praktischen Reglerentwurf. Fachbuchverlag Leipzig, München 2004, ISBN 3-446-22377-0, S. 141–143.

[Schönfeld-10] Rolf Schönfeld: Regelungen und Steuerungen in der Elektrotechnik. Verlag Technik, Berlin, München 1993, ISBN 3-341-01027-0, S. 78–96, 151–154.