Magnus-Effekt

Der Magnus-Effekt,[1] benannt nach Heinrich Gustav Magnus (1802–1870), ist ein Phänomen der Strömungsmechanik und beschreibt die Querkraftwirkung (Kraft), die ein rotierender runder Körper (Zylinder oder Kugel) in einer Strömung erfährt. Beschrieben wurde der Effekt schon 100 Jahre vor Magnus von Benjamin Robins,[2] der die Ursache bereits in der Rotation vermutete. Magnus gelang als Erstem eine physikalische Erklärung des Effektes.

Geschichte

Visualisierung des Magnus-Effekts im Strömungskanal

Magnus erbrachte 1852 den Nachweis des Phänomens rein experimentell und erkannte damit die Ursache für die Bahnabweichung rotierender Geschosse. Angeregt durch die Flugbahnabweichung von Tennisbällen gelang erst 1877 Lord Rayleigh die theoretische Begründung des Effekts.[3] Er schrieb die Entdeckung und Erklärung des Phänomens Magnus zu, obwohl diese bereits etwa 100 Jahre vorher von Robins[4] beschrieben wurde.[5] Erst 1959 erweiterte Briggs die bis dahin gültige Erklärung des Phänomens allein über die Bernoulli-Relation, indem er die Grenzschichttheorie einbezog, die Anfang des 20. Jahrhunderts vornehmlich von Ludwig Prandtl entwickelt wurde. Noch bis in das 21. Jahrhundert wurde an der Perfektion von Geschossformen bezüglich des Magnus-Effekts und in Verbindung mit der Haackschen Ogive weitergearbeitet.[6]

Prinzip

Der Klassiker seit Magnus

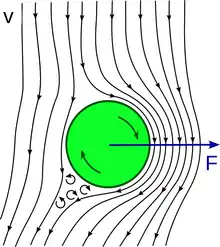
Ein rotierender Körper mit Zylindersymmetrie (z. B. Zylinder oder Kugel) wird im rechten Winkel zur Anströmrichtung V abgelenkt

Magnus erklärte den Effekt als erster[7] anhand der Bernoulli-Gleichung, die eine Relation zwischen Druck- und Geschwindigkeitsfeld einer reibungs-, viskositäts- und wirbelfreien Strömung herstellt. Um das experimentell gefundene Geschwindigkeitsfeld[8] zu beschreiben, überlagerte Magnus zwei Geschwindigkeitsfelder: Die symmetrische Umströmung eines nicht rotierenden Zylinders und die wirbelfreie Zirkulationsströmung um einen in ruhender Luft rotierenden Zylinder. Wo die Stromlinien eng beieinander liegen, ist die Geschwindigkeit höher als andernorts. In der Summe ist die Strömungsgeschwindigkeit auf der Seite des Zylinders, die sich mit der Anströmung dreht, größer als auf der anderen Seite und nach Bernoulli der Druck kleiner, sodass der Zylinder eine Kraft im rechten Winkel zur Anströmrichtung erfährt.

Robins[9] wies den Effekt mit Hilfe kugelförmiger Geschosse aus Musketen nach, deren Läufe leicht seitlich gebogen waren. Hierdurch rollt die Kugel im Lauf seitlich an der äußeren Seite bezüglich der seitlichen Biegung des Laufes, und die Kugel erhält einen Drall um die Hochachse. Nach Verlassen des Laufes wird die Kugel deutlich zur Seite abgelenkt.

Diese Erklärung für den Magnus-Effekt ist erfolgreich in dem Sinne, dass sie sich noch heute für den allgemeinen Fall des dynamischen Auftriebs in der Standardliteratur der Physik findet.[10][11] Als sehr spezielle Anwendung des Energiesatzes beschreibt die Bernoulli-Relation jedoch nicht Ursache und Wirkung, sondern ausschließlich einen funktionalen Zusammenhang zwischen Geschwindigkeits- und Druckfeld.

Erweiterungen bei Einbeziehung der Grenzschicht und Viskosität

Lyman Briggs erweiterte 1959 die Theorie von Magnus um den Einfluss der Grenzschicht:[12] In der Grenzschicht entsteht durch Reibung an der Kugeloberfläche eine Zirkulationsströmung, und auf der strömungsabgewandten Seite der Kugel löst sich die Luft aus der Grenzschicht (Grenzschichtablösung). Dadurch entsteht außerhalb der Grenzschicht eine Strömung, die der Bernoulli-Relation genügt.

Rotiert die umströmte Kugel nicht, erfolgt die Grenzschichtablösung symmetrisch. Der Magnus-Effekt entsteht dadurch, dass bei rotierender Kugel die Grenzschichtablösung auf einer Seite der Kugel später erfolgt, nämlich jener, wo die Strömung gleichgerichtet mit der Drehrichtung der Kugel ist. Hierdurch erhält die Strömung einen Impuls in Richtung der Seite der Kugel, die entgegen der Strömung dreht. Die Gegenkraft hierzu ist die seitliche Ablenkungskraft der Kugel. Im abgebildeten Beispiel verändert eine rechtsdrehende Kugel die Strömungsrichtung leeseits asymmetrisch nach einer Seite, während sie zur anderen Seite hin abgelenkt wird.

Praktische Beispiele

Flettner-Rotor als Schiffsantrieb

Die folgenden Beispiele von abgelenkten Flugkörpern werden häufig mit dem Magnus-Effekt in Verbindung gebracht. In allen Fällen treten jedoch verschiedene Effekte gleichzeitig auf. Es ist nicht offensichtlich, in welchem Ausmaß der Magnus-Effekt eine Rolle spielt.

Fußballspieler schießen den Ball mit Effet, damit er in einem Bogen ins Tor fliegt. Je schneller er dreht, umso größer ist die Bahnablenkung („Bananenflanke“).
Tischtennisspieler und Tennisspieler nutzen den Effekt, zum Beispiel beim Topspin und Slice
Curveballs im Baseball oder Riseballs im Softball
Spin bowling im Cricket
Flettner-Rotoren: In den 1920er- und 1930er-Jahren nutzte Anton Flettner den Magnus-Effekt zum Antrieb von Schiffen aus. Anstelle von Segelmasten besaßen die Schiffe große rotierende Zylinder. Trotz der maschinell angetriebenen Zylinder handelte es sich jedoch um Segelschiffe, die auf herrschenden Wind aus günstiger Richtung angewiesen waren. In den letzten Jahren gibt es wieder vermehrt Schiffe, die diese Art von Segel nutzen, wie etwa der 2010 in Dienst gestellte Frachter E-Ship 1.

Im Berliner Magnus-Haus kann der Effekt interaktiv erprobt werden, und eine Tafel erläutert den Vorgang:

Modell zum Magnus-Effekt
Texttafel

Siehe auch

Literatur

G. Magnus: Ueber die Abweichung der Geschosse, und: Ueber eine auffallende Erscheinung bei rotirenden Körpern. In: Annalen der Physik und Chemie. Bd. 28, Verlag von Johann Ambrosius Barth, Leipzig 1853, S. 1–28. (Volltext in der Google-Buchsuche)
G. Magnus: Ueber die Abweichung der Geschosse und über eine auffallende Erscheinung bei rotirenden Körpern. In: Die Fortschritte der Physik im Jahre 1853. Bd. 9, Berlin 1856, S. 78–84. (Volltext in der Google-Buchsuche)
Ludwig Bergmann, Clemens Schaefer, Thomas Dorfmüller, Wilhelm T. Hering: Lehrbuch der Experimentalphysik. Bd. 1: Mechanik, Relativität, Wärme. de Gruyter, 1998, ISBN 3-11-012870-5, S. 545 ff. (Fluidmechanische Kräfte an rotierenden Körpern in der Google-Buchsuche)
Jearl Walker: Der fliegende Zirkus der Physik. Oldenbourg Wissenschaftsverlag, 2007, ISBN 978-3-486-58067-9, S. 92–94. (Beispiele für Magnus-Effekt in der Google-Buchsuche)
Thorsten Kray: Untersuchungen über die Strömungsvorgänge bei rotierenden glatten Kugeln und Fußbällen. Dissertation. Universität Siegen 2008, online auf d-nb.info, abgerufen am 24. Januar 2017 (PDF; 9,8 MB).

Einzelnachweise

Gustav Magnus: Ueber die Abweichung der Geschosse, und: Ueber eine auffallende Erscheinung bei rotirenden Körpern. Aus der Abhandlung der Königlichen Akademie der Wissenschaften zu Berlin für 1852, in: Annalen der Physik und Chemie. Band LXXXVIII, Nr. 1, Berlin 1853, online auf Uni-Jena.de, abgerufen am 24. Januar 2017 (PDF; 1,46 MB).
Magnus, 1852: „Robins, der zuerst eine Erklärung der Abweichung in seinen Principles of Gunnery versucht hat, glaubte, daß die ablenkende Kraft durch die Eigendrehung des Geschosses erzeugt werde, und gegenwärtig nimmt man dies allgemein an.“
Lord Rayleigh: On the irregular flight of a tennis ball. In: Scientific Papers. I, 344, S. 1869–1881.
Benjamin Robins: New principles of gunnery. Hutton, London 1742.
H. M. Barkla, L. J. Auchterlonie: The Magnus or Robins effect on rotating spheres. In: Journal of Fluid Mechanics. Bd. 47, Ausg. 3, Cambridge Juni 1971, S. 437–447, doi:10.1017/S0022112071001150, online auf Cambridge.org, abgerufen am 24. Januar 2017.
Paul Weihnacht: VIRTUAL WIND TUNNEL METHOD FOR PROJECTILE AERODYNAMIC CHARACTERIZATION, 2007 (PDF, 211 kB) (Memento vom 10. Mai 2018 im Internet Archive)
Magnus, 1852: „Allein wiewohl man seit Robins sich sehr vielfältig bemüht hat zu erklären, wie durch eine solche Rotation eine Abweichung des Geschosses eintreten könne, so hat dies doch selbst den Bemühungen von Euler und Poisson nicht gelingen sollen.“
Magnus 1852, S. 6: „Kleine Windfahnen, die sehr beweglich waren, dienten dazu die Veränderungen des Drucks anzuzeigen, welche während der Rotation des Cylinders in dem Luftstrome stattfanden […] Wurde der Cylinder nicht gedreht, so nahmen beide Fahnen die Richtung des Luftstroms an. Sobald der Cylinder aber zu rotiren begann, so wandte sich auf der Seite, wo derselbe sich in gleicher Richtung mit dem Luftstrom bewegte, die Fahne dem Cylinder zu, während sie auf der anderen, wo die Bewegung des Cylinders und des Luftstroms in entgegengesetzter Richtung stattfanden, abgewandt wurde. Es war folglich auf jener Seite ein geringerer, auf dieser ein größerer Luftdruck vorhanden als im Zustand der Ruhe.“
Siehe auch: R. G. Watts, R. Ferrer: The lateral force on a spinning sphere. In: Am. J. Phys. 55(1), 1987, S. 40, doi:10.1119/1.14969.
Zum Beispiel: Lexikon der Physik. Spektrum, Akad. Verlag, Heidelberg 1999, ISBN 3-86025-293-3.
P. A. Tippler: Physik. Spektrum, Akad. Verlag, Heidelberg / Berlin / Oxford 1994, ISBN 3-86025-122-8.
Lyman J. Briggs: Effect of Spin and Speed on the Lateral Deflection (Curve) of a Baseball; and the Magnus Effect for Smooth Spheres. In: American Journal of Physics. Bd. 27, Ausg. 8, November 1959, S. 589, doi:10.1119/1.1934921, online auf AAPT, abgerufen am 24. Januar 2017.

Weblinks

Commons: Magnus-Effekt – Sammlung von Bildern, Videos und Audiodateien

Dirk Rathje: Wieso ist die Bananenflanke krumm? Auf: WeltDerPhysik.de, 10. März 2006.
Martin Kölling: Erneuerbare Energien in Fernost: vom Winde verweht. In: Technology Review. 12. Oktober 2007. (Nutzung des Magnus-Effekts zur Stromerzeugung (Windgeneratoren))
iCar 101 Kleinflugzeug durch Magnus-Effekt angetrieben (englisch)
Surprising Applications of the Magnus Effect. YouTube-Video zum Magnus-Effekt (englisch)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Gustav Magnus: Ueber die Abweichung der Geschosse, und: Ueber eine auffallende Erscheinung bei rotirenden Körpern. Aus der Abhandlung der Königlichen Akademie der Wissenschaften zu Berlin für 1852, in: Annalen der Physik und Chemie. Band LXXXVIII, Nr. 1, Berlin 1853, online auf Uni-Jena.de, abgerufen am 24. Januar 2017 (PDF; 1,46 MB).

[2] Magnus, 1852: „Robins, der zuerst eine Erklärung der Abweichung in seinen Principles of Gunnery versucht hat, glaubte, daß die ablenkende Kraft durch die Eigendrehung des Geschosses erzeugt werde, und gegenwärtig nimmt man dies allgemein an.“

[3] Lord Rayleigh: On the irregular flight of a tennis ball. In: Scientific Papers. I, 344, S. 1869–1881.

[4] Benjamin Robins: New principles of gunnery. Hutton, London 1742.

[5] H. M. Barkla, L. J. Auchterlonie: The Magnus or Robins effect on rotating spheres. In: Journal of Fluid Mechanics. Bd. 47, Ausg. 3, Cambridge Juni 1971, S. 437–447, doi:10.1017/S0022112071001150, online auf Cambridge.org, abgerufen am 24. Januar 2017.

[Nr.1-6] Paul Weihnacht: VIRTUAL WIND TUNNEL METHOD FOR PROJECTILE AERODYNAMIC CHARACTERIZATION, 2007 (PDF, 211 kB) (Memento vom 10. Mai 2018 im Internet Archive)

[7] Magnus, 1852: „Allein wiewohl man seit Robins sich sehr vielfältig bemüht hat zu erklären, wie durch eine solche Rotation eine Abweichung des Geschosses eintreten könne, so hat dies doch selbst den Bemühungen von Euler und Poisson nicht gelingen sollen.“

[8] Magnus 1852, S. 6: „Kleine Windfahnen, die sehr beweglich waren, dienten dazu die Veränderungen des Drucks anzuzeigen, welche während der Rotation des Cylinders in dem Luftstrome stattfanden […] Wurde der Cylinder nicht gedreht, so nahmen beide Fahnen die Richtung des Luftstroms an. Sobald der Cylinder aber zu rotiren begann, so wandte sich auf der Seite, wo derselbe sich in gleicher Richtung mit dem Luftstrom bewegte, die Fahne dem Cylinder zu, während sie auf der anderen, wo die Bewegung des Cylinders und des Luftstroms in entgegengesetzter Richtung stattfanden, abgewandt wurde. Es war folglich auf jener Seite ein geringerer, auf dieser ein größerer Luftdruck vorhanden als im Zustand der Ruhe.“

[9] Siehe auch: R. G. Watts, R. Ferrer: The lateral force on a spinning sphere. In: Am. J. Phys. 55(1), 1987, S. 40, doi:10.1119/1.14969.

[10] Zum Beispiel: Lexikon der Physik. Spektrum, Akad. Verlag, Heidelberg 1999, ISBN 3-86025-293-3.

[11] P. A. Tippler: Physik. Spektrum, Akad. Verlag, Heidelberg / Berlin / Oxford 1994, ISBN 3-86025-122-8.

[12] Lyman J. Briggs: Effect of Spin and Speed on the Lateral Deflection (Curve) of a Baseball; and the Magnus Effect for Smooth Spheres. In: American Journal of Physics. Bd. 27, Ausg. 8, November 1959, S. 589, doi:10.1119/1.1934921, online auf AAPT, abgerufen am 24. Januar 2017.