Idealer Tiefpass

Ein idealer Tiefpass, auch als si-Filter, gelegentlich als Küpfmüller-Tiefpass (KTP)[1][2] und im englischen meist als Sinc-Filter bezeichnet, ist in der Signalverarbeitung ein Tiefpass mit der folgenden idealen Übertragungsfunktion: Unterhalb einer bestimmten Grenzfrequenz mit der Bandbreite B werden alle Frequenzanteile durch das Filter hindurchgelassen, oberhalb der Grenzfrequenz B werden alle Frequenzanteile blockiert. Der ideale Tiefpass spielt als Modell in der Filtertheorie eine wichtige Rolle, beispielsweise beim Nyquist-Shannon-Abtasttheorem.

Ein idealer Tiefpassfilter ist in der Theorie gut beschreibbar, in Praxis allerdings nicht realisierbar. Dies liegt an der nichtkausalen und unendlich langen Impulsantwort. Ein idealer Tiefpassfilter zeigt am Ausgang des Filters bereits eine Reaktion, bevor das auslösende Signal am Filtereingang anliegt. Reale Tiefpassfilter nähern sich daher der Übertragungsfunktion des idealen Tiefpass nur an, erreichen sie aber nie, da sie sonst eine unendliche Gruppenlaufzeit hätten.

Übertragungsfunktion

Normierte Übertragungsfunktion H(f)

Normierte Impulsantwort h(t)

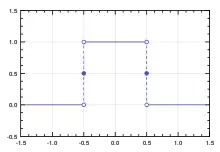
Mathematisch kann die Übertragungsfunktion des idealen Tiefpasses im zeitkontinuierlichen Fall mit der Rechteckfunktion und der Bandbreite B und dem Parameter der Frequenz f beschrieben werden als:

H(f)={\text{rect}}\left({\frac {f}{2B}}\right)

Im Zeitbereich ergibt sich als inverse Fourier-Transformierte der Übertragungsfunktion die Impulsantwort h(t):

h(t)={\mathcal {F}}^{-1}\{H\}(t)=2B\cdot {\frac {\sin(2\pi Bt)}{2\pi Bt}}=2B\cdot \mathrm {si} (2\pi Bt)

Die dabei auftretende Funktion si wird auch als si-Funktion oder Sinc-Funktion bezeichnet, wovon sich für zeitkontinuierliche Filter die Bezeichnung Sinc-Filter ableitet.

Im zeitdiskreten Fall, beispielsweise in der digitalen Signalverarbeitung, liegen über die Zeit bzw. das Spektrum keine kontinuierlichen Verläufe vor, sondern diskrete Folgen. Dabei wird die oben dargestellte Rechteckfunktion durch eine endliche Rechteckfolge mit N Spektralpunkten ersetzt. Die inverse Fouriertransformation wird durch die inverse diskrete Fourier-Transformation (IDFT) ersetzt. Damit tritt durch die periodische Fortsetzung im Zeitbereich in der dann zeitdiskreten Impulsantwort h(x) keine si-Funktion auf, sondern ein Dirichlet-Kern. Dieser wird in Anlehnung an die si-Funktion auch als di-Funktion bezeichnet und folgendermaßen definiert:

\mathrm {di} _{N}(x)={\frac {\sin((N+{\frac {1}{2}})x)}{\sin({\frac {1}{2}}x)}}

Gelegentlich werden in der meist englischsprachigen Fachliteratur auch im zeitdiskreten Fall ideale Tiefpassfilter als Sinc-Filter bezeichnet.

Einzelnachweise

Nocker, Rudolf: Digitale Kommunikationssysteme. 1. Grundlagen der Basisband-Übertragungstechnik. Vieweg, 2004, ISBN 978-3-528-03976-9.
Hoffmann, Rüdiger: Signalanalyse und -erkennung: Eine Einführung für Informationstechniker. Springer, 1998, ISBN 978-3-540-63443-0.

Literatur

Karl-Dirk Kammeyer: Nachrichtenübertragung. 2. Auflage. Teubner, 1996, ISBN 3-519-16142-7.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Nocker, Rudolf: Digitale Kommunikationssysteme. 1. Grundlagen der Basisband-Übertragungstechnik. Vieweg, 2004, ISBN 978-3-528-03976-9.

[2] Hoffmann, Rüdiger: Signalanalyse und -erkennung: Eine Einführung für Informationstechniker. Springer, 1998, ISBN 978-3-540-63443-0.