15-Puzzle
Das 15-Puzzle, auch Fünfzehnerspiel, 14-15-Puzzle, Schiebepuzzle, Schieberätsel, Schiebefax oder Ohne-Fleiß-kein-Preis-Spiel genannt, ist ein Geduldsspiel. Es wurde zwischen 1870 und 1880 in den Vereinigten Staaten vom Postangestellten Noyes Palmer Chapman erfunden. Das Spiel besteht aus 15 Kacheln, von 1 bis 15 durchnummeriert, die auf den 16 Feldern eines Vier-mal-vier-Quadrats angebracht sind. Ein Feld (das „Loch“) bleibt also frei. Eine (vertikal oder horizontal) benachbarte Kachel kann jeweils in das freie Feld hineingeschoben werden. Die Aufgabe besteht nun darin, durch Verschieben der Kacheln die Zahlen von 1 bis 15 aufsteigend anzuordnen.
Je nach Ausgangsstellung gibt es verschiedene Varianten des Spiels, insbesondere das 14-15-Puzzle, bei dem in der Ausgangsstellung lediglich die Zahlen 14 und 15 vertauscht sind, wodurch das Puzzle unlösbar wird. Heutige Ausgaben des Spiels werden meist in der gewünschten Anordnung ausgeliefert; Der Spieler verschiebt („mischt“) die Kacheln zunächst und versucht dann, das Puzzle wieder in die geordnete Ausgangsstellung zu bringen. Bei dieser Spielvariante ist mithin garantiert, dass die Aufgabe lösbar ist.
Geschichte
Das Spiel wurde von dem Postangestellten Noyes Palmer Chapman erfunden, der seinen Freunden im Jahr 1874 ein ähnliches Puzzle zeigte. Bei diesem ging es darum, 16 nummerierte Blöcke in die Form eines magischen Quadrates zu bringen. Die ersten Kopien des 15-Puzzles gelangten nach Syracuse im Staat New York zu Frank Chapman, dem Sohn von Noyes. Von dort verbreitete sich das Spiel weiter nach Watch Hill und schließlich nach Hartford in Connecticut, wo Schüler der amerikanischen Schule für Hörbehinderte das Puzzle in großen Auflagen fertigten und im Dezember 1879 als Weihnachtsgeschenke in Boston, Massachusetts verkauften. Matthias Rice, der Besitzer eines Geschäftes für ausgefallene Holzgegenstände, entdeckte eines dieser Puzzles und fing an, diese umgehend selbst herzustellen und als „Gem Puzzle“ auf den Markt zu bringen.
Die 15 Spielsteine bzw. Kacheln lagen dabei lose in einer kleinen Box und die Spielanleitung lautete: »Place the blocks in the box irregularly, then move until in regular order« (zu Deutsch etwa: „Setze die Spielsteine in beliebiger Anordnung in die Box, dann verschiebe sie, bis sie sich in Reihenfolge befinden“).[1]
Gegen Ende Januar 1880 setzte der Zahnarzt Charles Pevey ein Preisgeld für die Lösung des 15-Puzzles aus. Der erste Trend für das Spiel war in den USA im Februar, in Kanada im März und in Europa im April 1880 zu sehen. Der Trend war bereits im Juli desselben Jahres aber wieder im Rückgang. Erst neun Jahre später wurde das Spiel in Japan eingeführt.[2]
Chapman wollte das 15-Puzzle am 21. Februar 1880 als „Block Solitaire Puzzle“ zum Patent anmelden, stieß beim Patentamt aber auf Ablehnung, da sich sein Spiel nicht ausreichend von dem am 20. August 1878 erteilten Patent für das von Ernest U. Kinsey entwickelte Spiel „Puzzle-Blocks“ zu unterscheiden schien.[2]
Der Rätselspezialist Samuel Loyd behauptete von 1891 bis zu seinem Tod im Jahr 1911, dass er der Erfinder dieses Rätsels sei, konnte dies aber niemals belegen. Neueren Untersuchungen zufolge wurde er sogar als Lügner entlarvt.[2][3] Während des Ersten Weltkriegs wurde das 15-er Puzzle als „Geduldspiel für den Schützengraben“ produziert.
Aufgabenstellungen
Ursprüngliches Puzzle
Beim „Gem Puzzle“, das Matthias Rice 1879 produzierte und verkaufte,[1] nahm der Spieler zu Beginn die Steine heraus und setzte sie beliebig in die Box. Anschließend bestand die Aufgabe darin, durch Verschieben der Steine die Zahlen zeilenweise aufsteigend anzuordnen. Dabei ergeben sich folgende mathematische Zusammenhänge:
- Es gibt 16! = 20922789888000 ≈ 2,1 ⋅ 1013 mögliche Start-Anordnungen (Permutationen der Zahlen 1 bis 16), bei denen das leere 16-te Feld nicht unbedingt unten rechts sitzt.
- Durch Verschieben der Steine kann genau die Hälfte aller Startanordnungen in eine aufsteigende Reihenfolge (Sequenz) mit dem leeren Feld unten rechts gebracht werden.[4][5]
- Durch Verschieben der Steine kann die andere Hälfte aller Startanordnungen in eine Sequenz mit dem leeren Feld oben links gebracht werden.
- Bei einer Startanordnung, mit der eine Sequenz mit dem leeren Feld oben links erreichbar ist, kann man einer Sequenz mit dem leeren Feld unten rechts lediglich so nahe bringen, dass sich nur zwei der fünfzehn Blöcke an den falschen Positionen befinden.
Für andere Zielanordnungen kann man folgende Sachverhalte feststellen:
- Lässt sich eine bestimmte Anordnung erreichen, so ist
- die horizontal oder vertikal gespiegelte Anordnung nicht erreichbar.
- die um 90° nach rechts oder links gedrehte Anordnung nicht erreichbar.
- die um 180° gedrehte Anordnung ebenfalls erreichbar.
- die diagonal gespiegelte Anordnung erreichbar.
- eine Anordnung, bei der nur zwei benachbarte Steine vertauscht sind, nicht erreichbar.
Die Hälfte (H1) aller Ausgangsstellungen lässt sich in diese Anordnung bringen.
Die andere Hälfte (H2) der Ausgangsstellungen lässt sich in diese Anordnung bringen.
Jede zweite Ausgangsstellung (H1) lässt sich nur in diese Anordnung bringen.
Die andere Hälfte (H2) lässt sich nur in diese Anordnung bringen.
15-14-Puzzle
In der Ausgangsposition des 15-14-Puzzles sind die Steine mit Ausnahme der Steine 14 und 15 schon in aufsteigender Reihenfolge sortiert. Das letzte Feld unten rechts bleibt frei. Bei dieser Ausgangsstellung ist die Aufgabe, die Zahlen durch Verschieben der Steine in die richtige Reihenfolge zu bringen, wobei das letzte Feld wieder frei bleibt, nicht lösbar. Die Aufgabe wird lösbar, wenn man das erste statt des letzten Feldes freilässt (s. o.)
14-15-Puzzle
Eine weitere Möglichkeit besteht darin, aus der geordneten Reihenfolge mit der Lücke unten rechts bestimmte andere Anordnungen zu erreichen, z. B:
- Ausgangsstellung
Erreichbar:
Vertikale Anordnung
Erreichbar:
Eine Spirale
Erreichbar:
Diese Zick-Zack-Anordnung.
Erreichbar:
Dieser Springerpfad
Nicht erreichbar:
Eine Drehung um 90°.
Modernes 15-Puzzle
Viele der Spiele, die heute erhältlich sind, sind im Auslieferungszustand bereits richtig sortiert und ihre Steine sind miteinander so verzahnt, dass man sie zwar verschieben, aber nicht entnehmen kann. Das Ziel des Spieles ist es von daher, ein gemischtes Puzzle wieder in den Originalzustand zu versetzen.
Im Handel findet man viele Formen dieses Spiels. Es gibt sie beispielsweise als Schlüsselanhänger aus Plastik oder Holz gefertigt.
Es gibt auch Spiele, die nicht mehr das Ziel haben, Zahlen zu sortieren, sondern aus einem Bild bestehen, das nur komplett zu sehen ist, wenn alle Quadrate in einer richtigen Reihenfolge sortiert werden.
Es gibt Ausführungen mit Buchstaben oder Buchstabengruppen statt Zahlen. Hier soll als Lösung entweder die alphabetische Reihenfolge erreicht werden oder es soll ein bestimmter Text stehen. Letztere haben oft ein Paar (oder gar mehrere) gleicher Kacheln (d. h. mit gleichen Buchstaben). Kommt es dabei zu einer Situation, bei der nur noch die beiden letzten Kacheln vertauscht sind, so muss man ein Paar gleicher Buchstaben tauschen, um die Aufgabe zu lösen. Steht beispielsweise bei dem in der Abbildung „Textversion“ dargestellten Spiel in der unteren Zeile „Prsei“ statt „Preis“, so muss man entweder die beiden „e“, die beiden „n“ oder (!) die beiden „ei“ tauschen.
Bei der Darstellung mittels römischer Zahlen erhöht sich der Schwierigkeitsgrad durch die meist schlechtere Übung bei der Zahlenfolge.
Version mit Buchstaben
Version mit Text
Version mit Bild
Version mit römischen Zahlen
15-Puzzle als Schlüsselanhänger
Magische Quadrate
Eine weitere Aufgabenstellung für das 15-Puzzle mit Zahlen ist es, die übliche Start-Anordnung (mit dem leeren Feld unten rechts) in ein magisches Quadrat zu überführen, wobei das leere Feld für die Zahl 0 steht.[6] Die magische Summe (d. h. die Zeilen-, Spalten- und Diagonalensumme) ist dann 30. Berücksichtigt man Drehungen oder Spiegelungen des Quadrats, gibt es 880 8 = 7040 magische Quadrate auf einem 4x4 -Feld. Von diesen ist genau die Hälfte, also 3520, aus der üblichen Start-Anordnung zu erreichen. Kociemba bestimmte für jedes dieser magischen Quadrate die minimale Anzahl von Zügen, die ausgehend von der Start-Anordnung erforderlich ist. Man benötigt mindestens 35 Züge, um ein magisches Quadrat zu erhalten, und es gibt nur ein einziges magisches Quadrat, das in 35 Zügen erreichbar ist.[7]
Andere Größen
Es gibt auch Ausführungen in anderen Größen, so z. B. das 8-Puzzle in einem Drei-mal-drei-Quadrat und das 31-Puzzle in einem Vier-mal-acht-Rechteck.
Mathematischer Hintergrund
Permutationen und Invarianten
Jede Stellung des Spiels ist entweder lösbar oder unlösbar, das heißt, sie kann in die Endstellung überführt werden oder nicht. Zum Beweis wird die so genannte Parität jeder Stellung betrachtet. Sie bleibt bei einem Zug immer erhalten. Die Parität ergibt sich aus der Anzahl der ungeordneten Zahlenpaare. Dabei ist die Anzahl der Zahlenpaare, die sich in falscher Reihenfolge befinden und die Nummer der Reihe, in der sich das leere Feld befindet. Die Summe ist entweder gerade oder ungerade. Bei allen erlaubten Zügen bleibt diese Parität erhalten, das heißt eine gerade Spielstellung kann nie in eine ungerade überführt werden und umgekehrt. Da die ursprüngliche Aufgabenstellung ungerade ist, kann sie nie in den geraden Endzustand führen.
Eine andere Beweisidee verwendet das Vorzeichen der als Permutation, also als Vertauschung, betrachteten Stellung, das mit jedem Zug das Vorzeichen wechselt.
Beispiel
Um zu überprüfen, ob eine Konstellation von Steinen mittels erlaubter Züge in eine andere überführt werden kann, ist zwischen Rahmengrößen mit geradzahliger (wie der vorliegenden) und solchen mit ungeradzahliger Spaltenanzahl zu unterscheiden. Grundvoraussetzung ist, dass die Quadrate in der gezeigten Weise nummeriert sind oder bei Puzzles, deren Lösung in der Erstellung eines Bildes liegt, für den Nachweis nummeriert werden. Bei Puzzles, die mehrere Lösungen erlauben, etwa Symbole, die nach bestimmten Regeln angeordnet werden sollen, ist nachzuweisen, dass keine der Lösungsvarianten durch erlaubte Züge erreicht werden kann.
Zur Ermittlung des Unordnungsparameters N1 zählt man alle Zahlenpaare, bei denen eine kleinere Zahl auf eine größere folgt, gleich wie viele Steine dazwischen liegen; die absolute Größe der jeweiligen Zahlen ist unerheblich, Zahlen können in mehreren Paaren vorkommen. Verglichen werden die Steine so, als wären alle in einer horizontalen Reihe aufgelistet. Bei einer Konstellation von beispielsweise 1, 4, 2, 6, 7, 8, 3, 5 gibt es also folgende Paare (2|4), (3|8), (3|7), (3|6), (3|4), (5|8), (5|7), (5|6). Man iteriert von links nach rechts und vergleicht eine Zahl mit allen links stehenden Zahlen. Sobald eine links stehende Zahl dann größer ist, wurde ein unordentliches Paar gefunden.
Wird ein Stein in horizontaler Richtung verschoben, ändern sich weder der Unordnungsparameter N1 noch der Reihenparameter N2, da man diese Bewegung als Austausch des bewegten Steins durch das freie Feld auffassen kann, das in der Berechnung des Unordnungsparameters nicht berücksichtigt wird.
Wird ein Stein in vertikaler Richtung verschoben, ändert sich der Reihenparameter N2 um +/− 1. Die vertikale Verschiebung betrifft immer genau drei Zahlenpaare, denn es kann nur Änderungen in der Ordnung zwischen dem verschobenen Stein und den drei eingeschlossenen Feldern geben. Dabei hat sich für jeden eingeschlossenen Stein der Unordnungsparameter um 1 vergrößert oder verkleinert, da der zu verschiebende Stein seinen Platz getauscht hat, haben nun alle Paare, welche mit dem verschiebenden Stein gebildet wurden, ihre Ordnung geändert. Unordentliche Paare sind nun ordentliche und umgekehrt.
In dieser Konstellation beträgt N1=3; die unordentlichen Paare sind .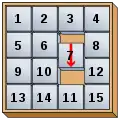
Die 7 wechselt vertikal auf das leere Feld, wodurch N1 um drei erhöht und N2 um eins erniedrigt wird.
N war von Anfang an gerade (N=4). Da der Reihenparameter N2 bei jedem vertikalen Schritt eine ungerade Veränderung erfährt (+1, −1) und der Ordnungsparameter N1 dann ebenfalls nur eine ungerade Veränderung erfährt (+3, +1, −1, −3), kann N jeweils nur eine gerade Änderung erfahren (+4, +2, 0, −2, −4). Es ist also nicht möglich, von der ursprünglichen Aufgabenstellung (15 mit 14 getauscht) in eine sortierte Reihenfolge zu gelangen, da die ursprüngliche Reihenfolge (N = 5) eine ungerade Parität hat und nicht mit dem Verschieben von Steinen in eine gerade Parität überführt werden kann.
Allgemeinfall
In einem a × a großen Puzzle mit ungeradzahliger Spaltenanzahl a beträgt die Anzahl der eingeschlossenen Steine a²−1, also eine gerade Zahl; der Unordnungsparameter ändert sich also mit einem horizontalen Zug gar nicht und mit einem vertikalen Zug um eine gerade Zahl. Die Parität des Unordnungsparameters N1 bleibt mit jedem Zug erhalten.
In einem a × a großen Puzzle mit geradzahliger Spaltenanzahl a (wie dem vorliegenden) beträgt die Anzahl der eingeschlossenen Steine a²−1, also eine ungerade Zahl, der Unordnungsparameter N1 ändert sich mit einem vertikalen Zug um eine ungerade Zahl. Der Reihenparameter N2 vergrößert oder verkleinert sich mit jedem vertikalen Zug um 1; N1+N2 ist also die Summe aus zwei ungeraden Zahlen und damit gerade. Die Parität von (N1+N2) bleibt mit jedem Zug erhalten.
Da die Parität von N1 bei ungeradzahliger oder (N1+N2) bei geradzahliger Spaltenanzahl stets erhalten bleibt, kann man durch einfaches Abzählen prüfen, ob eine zufällige Konstellation K1 in eine andere bestimmte Konstellation K2 mittels erlaubter Züge überführt werden kann. Bei der klassischen Aufgabenstellung des 15-Puzzles ist das nicht möglich, da bei geradzahliger Spaltenanzahl a=4 die Summe (N1+N2)=(1+4)=5 in (N1+N2)=(0+4)=4 überführt werden müsste.
Des Weiteren zeigen diese Überlegungen, dass höchstens die Hälfte aller denkbaren Konstellationen aus der Grundkonstellation heraus erreicht werden kann, weil nur Anordnungen von geraden in gerade oder ungeraden in ungerade Paritäten überführt werden können. Wie Story 1879 zeigte,[5] ist von der Grundkonstellation genau diese Hälfte immer erreichbar, was aber durch den hier vorgestellten Beweis nicht nachgewiesen werden kann, da die Parität lediglich eine notwendige, nicht aber eine hinreichende Bedingung für die allgemeine Lösbarkeit ist. Einen eleganten modernen Beweis dafür, dass alle Konstellationen von gerader Parität tatsächlich ineinander überführt werden können und auch alle Konstellationen mit ungerader Parität ineinander überführt werden können, gab Archer 1999.[8] Auch die im folgenden Kapitel angesprochenen Algorithmen für das 15-Puzzle belegen diese Tatsache.
Algorithmen und Komplexität
Schiebepuzzle wie das 8-Puzzle oder das 15-Puzzle dienen seit langem als Testprobleme für Suchalgorithmen in der Künstlichen Intelligenz.[9][10] Wie Brüngger et al. 1999 unter Verwendung eines Intel Paragon Parallelrechners mit 64 Knoten zeigten, erfordert die Lösung des 15-Puzzles für alle Start-Anordnungen maximal 80 Schritte[10]. Korf und Schultze[11] bestimmten 2005 mittels einer Breitensuche und unter Verwendung eines Parallelrechners für jede der 16!/2 = 10.461.394.944.000 lösbaren Start-Anordnungen die minimale Anzahl von Schritten, die zur Lösung notwendig ist. Insbesondere bestimmten sie erstmals alle 17 Start-Anordnungen, die in 80 Schritten (und nicht weniger) gelöst werden können. Eine zufällig gewählte, lösbare Ausgangskonfiguration lässt sich in durchschnittlich 52,6 Zügen lösen. Zur Vermeidung von Speicherfehlern – immerhin waren 8 1014 Bit ≈ 100 Terabyte zu schreiben und zu lesen – verwendeten Korf und Schultze ein RAID-System.
Ratner und Warmuth bewiesen 1990, dass das verallgemeinerte Problem, die minimale Anzahl Züge zu einer lösbaren Start-Anordnung in einem n x n -Spiel zu finden, NP-schwer ist.[12]
Literatur
- L. E. Horden: Sliding Piece Puzzles. Oxford University Press, 1986, ISBN 0-19-853204-0.
- Jerry Slocum, Dic Sonneveld: The 15 Puzzle. Slocum Puzzle Foundation, 2006, ISBN 1-890980-15-3.
Siehe auch
Weblinks
- The 14-15-Puzzle – Englischsprachige Seite, die den Beweis der Unlösbarkeit des ursprünglichen 15-Puzzles anhand interaktiver Beispiele illustriert.
- 15-Puzzle Optimal Solver mit Download (von Herbert Kociemba)
Einzelnachweise
- Jerry Slocum: Sam Loyd's Most Successful Hoax. (PDF; 672 kB). Vortrag auf Seventh Gathering for Gardner, März 2006, The Convention of the Association of Game and Puzzle Collectors. Publiziert in: E. Pegg, A. H. Schoen, T. Rodgers: Homage to a Pied Puzzler. A.K. Peters, Wellesley/ Massachusetts 2009, S. 3–21. (hier: S. 4)
- Jerry Slocum, Dic Sonneveld: The 15 Puzzle. Slocum Puzzle Foundation, 2006, ISBN 1-890980-15-3.
- Sam Loyd's Fifteen Englischsprachige Seite mit Java-Applet und Beweis der Unlösbarkeit des Problems. Abgerufen 16. November 2007.
- Woolsey Johnson: Notes on the „15“ Puzzle. I. In: Amer. J. Math. 2, 1879, S. 397 bis 399.
- William E. Story: Notes on the „15“ Puzzle. II. In: Amer. J. Math. 2, 1879, S. 399 bis 404.
- Sam Loyd, Martin Gardner: Mathematical puzzles of Sam Loyd. Dover Pubs., New York 1959, S. 19 und 20., Google Books
- Herbert Kociemba: 15-Puzzle Optimal Solver 2013.
- Aaron F. Archer: A Modern Treatment of the 15 Puzzle. In: The American Mathematical Monthly. 106, No. 9, 1999, S. 793 bis 799.
- Richard E. Korf, Larry A. Taylor: Finding Optimal Solutions to the Twenty-Four Puzzle. (PDF; 1,1 MB). In: Proceedings of the 11th National Conference on Artificial Intelligence. 1993, S. 756 bis 761.
- Adrian Brüngger, Ambros Marzetta, Komei Fukuda, Jurg Nievergelt: The parallel search bench ZRAM and its applications. (PDF; 192 kB). In: Annals of Operations Research. 90, 1999, S. 45 bis 63.
- Richard E. Korf, Peter Schultze: Large-Scale Parallel Breadth-First Search. (PDF; 104 kB). In: AAAI Conference On Artificial Intelligence. Proceedings of the 20th national conference on Artificial intelligence. 3, 2005, S. 1380 bis 1385, hier S. 1384 bis 1385 (Fifteen Puzzle), Table 2 (States as a Function of Depth for Fifteen Puzzle).
- D. Ratner, M. Warmuth: Finding a shortest solution for the (N X N)-extension of the 15-puzzle is intractable. In: Journal of Symbolic Computation. 10, 1990, S. 111 bis 137.