Mechanische Geduldspiele
Mechanische Geduldspiele oder Denk- oder Knobelspiele sind eine Kategorie von Rätsel-Spielen, in denen die Lösung des Problems durch Manipulation des ganzen Objektes oder von Teilen davon erfolgen muss. Die Spiele werden meistens für einen einzelnen Spieler konzipiert (sogenanntes Solitärspiel). Das Ziel ist es, dass der Spieler das Prinzip des Objektes durchschaut, und weniger, dass er durch die heuristische Methode Versuch und Irrtum zufällig auf die richtige Lösung kommt. Sie werden deshalb gerne auch als Intelligenztest oder in der Problemlösungsschulung verwendet.
Eines der bekanntesten Geduldspiele ist der von Ernő Rubik 1974 erfundene Zauberwürfel. Ein altes östliches Knobelspiel ist Tangram aus China, welches zwischen dem 8. und 4. Jahrhundert v. Chr. erfunden wurde. Das wahrscheinlich erste dokumentierte westliche mechanische Knobelspiel stammt aus dem 3. Jahrhundert v. Chr. aus Griechenland. Danach ist eine Vielzahl weiterer Spiele mit demselben Spielprinzip erfunden worden.
Geschichte
Ein erstes überliefertes Knobelspiel ist Tangram, welches zwischen dem 8. und 4. Jahrhundert v. Chr. in China entstanden ist. Dort müssen aus Plättchen, die aus einem Quadrat herausgeschnitten wurden, schattenrissartig Tiere, Schiffe oder andere Gestalten gelegt werden.
Das Stomachion ist ein Schriftstück des Archimedes (3. Jh. v. Chr.), das ein Legepuzzle zum Inhalt hat. Dort sollen 14 Teile zum Quadrat gefügt werden. Im Iran wurden Puzzle-Schlösser bereits im 17. Jahrhundert hergestellt. Die nächsten bekannten Spiele stammen aus Japan. Ein Buch aus dem Jahr 1742 erwähnt ein Spiel namens „Sei Shona-gon Chie No-Ita“. 1870 oder 1880 kam ein unlösbares Puzzlespiel auf den Markt, welches als 15-Puzzle bekannt wurde. Heute sind ähnliche, aber lösbare Puzzles in den Läden. 1820 hat sich das Tangram-Spiel in Europa und Amerika ausgebreitet. Die Firma Richter aus Rudolstadt produzierte ab 1882 große Mengen an Tangram-ähnlichen Spielen verschiedenster Form, die Anker-Puzzles. 1893 wurde von Professor Hoffman ein Buch unter dem Namen „Puzzles Old and New“ veröffentlicht. Es enthielt unter anderem mehr als 40 Beschreibungen für Puzzles mit geheimen Öffnungsmechanismen. Dieses Buch entwickelte sich zu einer Art Standardwerk für Knobelspiele. Moderne Auflagen existieren für diejenigen, die sich dafür interessieren. Auch sonst war die Wende zum 20. Jahrhundert eine Zeit, in der Knobelspiele groß in Mode waren. Erste Patente auf Puzzle-Designs wurden angemeldet. So zum Beispiel im Jahr 1890 ein Spiel von Wilhelm Altekruse, das aus 12 identischen Teilen bestand (siehe Bild). Mit der Erfindung von billig formbaren Materialien wie Plastik wurde die Tür zu weiteren Möglichkeiten geöffnet.
Varianten
Zusammensetzspiele
In dieser Kategorie liegt das Spiel in Einzelteilen vor und es muss eine Zielform erzeugt werden. Zu diesen Spielen gehören der Somawürfel von Piet Hein und die Pentominos von Solomon W. Golomb, außerdem Probleme, bei denen eine Anzahl Teile in eine (meist viel zu klein erscheinende) Kiste geräumt werden müssen, schließlich auch die Gruppe der Legepuzzles mit Tangram und die Legespiele des Ankerwerks in Rudolstadt. Weiterhin gibt es eine Puzzle-Reihe unter dem Namen Happy Cubes, wo aus zweidimensionalen Teilen dreidimensionale Objekte zusammengepuzzelt werden können.
Das Bild zeigt eine Variante von Hoffmans Packproblem. Packe 27 identische Quader mit den Kantenlängen A, B und C in eine kubische Box mit der (inneren) Kantenlänge A+B+C, wobei folgende zwei Bedingungen gelten müssen: A, B und C müssen unterschiedlich sein und die kleinste Seitenlänge muss größer als sein. Eine mögliche Variante für A, B und C sind 18, 20, 22. Die Box muss dann Innenmaße von 60 × 60 × 60 haben.
Moderne Maschinen, wie Lasercutter, ermöglichen es, komplexe 2-dimensionale Puzzles aus Holz oder Plexiglas zu schneiden. Von diesen Möglichkeiten wird in letzter Zeit vermehrt Gebrauch gemacht und Spiele mit außergewöhnlichen dekorativen geometrischen Mustern entworfen. Hier kann die ganze Vielfalt der möglichen regelmäßigen Flächenaufteilungen ausgenutzt werden.
Auch der Computer ist hilfreich für neue Ideen. Er erlaubt die erschöpfende Suche nach Lösungen. Mit seiner Hilfe kann das Spiel so entworfen werden, dass es möglichst wenige Lösungen hat und somit relativ kompliziert wird.
Die Arbeit mit transparenten Werkstoffen erlaubt Puzzles, bei denen die Teile übereinander gestapelt werden müssen. In der Lösung müssen dann Muster, Bilder oder Farbverläufe sichtbar sein. Es gibt beispielsweise ein Spiel, das aus einigen Scheiben besteht, auf denen einzelne Winkelabschnitte unterschiedlich eingefärbt sind. Diese Scheiben müssen so gestapelt werden, dass ein Farbkreis (Rot→Blau→Grün→Rot) um die Scheiben herum sichtbar wird.
Ein einfach zu realisierendes Spiel ist das Nagelspiel: Es besteht aus einer Anzahl von Nägeln. Die Aufgabenstellung gibt vor, dass alle Nägel von einem einzelnen Nagel getragen werden sollen. Die Lösung ist eine Konstruktion, in der sich die Nägel verzahnen und danach auf einem Nagelkopf balancieren.
Auseinandernehmspiele
Puzzles in dieser Kategorie sollen normalerweise geöffnet oder in mehrere Teile zerlegt werden. Zu dieser Sorte gehören die Kästchen mit geheimen Verschlussmechanismen, die der Knobelnde durch Probieren öffnen muss. Außerdem gehören in diese Kategorie auch Metallspiele, bei denen mehrere Teile ineinander verhakt sind.
Die zwei im Bild gezeigten Spiele sind besonders gut für den Kaffeetisch geeignet, da sie dem Spieler vorgaukeln, dass es doch ganz einfach sein müsse, sie zu zerlegen. Viele Menschen bekommen sie aber gar nicht auseinander. Das Problem liegt in der Form der Verzahnungen: Diese sind konisch und erlauben somit das Entfernen nur in eine Richtung. Diese Richtung ist bei allen Teilen gleich, so dass man die Teile immer nur ein wenig bewegen kann. Die eine Richtung wird durch den eigenen Zahn blockiert, da dieser dann durch seine konische Form in der Öse des vorherigen Teils steckt. In der anderen Richtung bleibt die eigene Öse im Zahn des nächsten Teils hängen.
Zu dieser Kategorie gehören auch die in Japan extrem beliebten Schachteln mit geheimen Öffnungsmechanismen. Diese Kästen enthalten mehr oder minder komplizierte, meist nicht sichtbare, Verschlussmechanismen, die schließlich einen kleinen Hohlraum freigeben. Die Mechanismen reichen dabei von kaum sichtbaren Paneelen, die verschoben werden müssen, über Kippmechanismen, Magnetverschlüsse, bewegliche Pins, die mit Rotationen in eine bestimmte Position gebracht werden müssen bis hin zu Zeitverschlüssen, in denen das Objekt in einer Position eine bestimmte Zeit festgehalten werden muss, bis eine Flüssigkeit ein Gefäß gefüllt hat.
Verzahnende Objekte
Verzahnende Puzzles sind zum Beispiel die bekannten chinesischen Holzknoten, die bisweilen auch Teufelsknoten[1] genannt werden. Die Aufgabe besteht darin, das Spiel zu zerlegen und dann wieder zusammenzusetzen. Beide Aktionen können kompliziert sein. Im Gegensatz zu den Zusammensetz-Puzzles haben verzahnende Puzzles die Eigenschaft, nicht einfach auseinanderzufallen. Der Schwierigkeitsgrad dieser Puzzles wird angegeben als Anzahl von Zügen, die notwendig sind, um beim Auseinandernehmen das erste Teil aus dem Puzzle zu entfernen. Das Bild zeigt den bekanntesten Vertreter dieser Kategorie, den chinesischen Holzknoten, bei dem 5 Bewegungen benötigt werden, bevor das erste Teil entfernt werden kann.
Solche Spiele lassen sich seit dem Anfang des 18. Jahrhunderts nachweisen. 1803 enthielt der Katalog von Georg Hieronimus Bestelmeier zwei Puzzles dieser Art. Anfang des 19. Jahrhunderts übernahmen die Japaner den Markt für diese Spiele. Sie entwickelten eine Vielzahl von Spielen in Form von Tieren, Häusern und anderen Objekten, wogegen die Entwicklung im westlichen Raum bei geometrischen Formen blieb. Mit Hilfe von Computern können Spiele, wie die chinesischen Holzknoten analysiert werden.
Stewart Coffin hat seit den 1960er Jahren viele Spiele auf der Grundlage des Rhombischen Dodekaeders, mit Sechskant- oder Dreikant-Leisten entwickelt. Seine Spiele haben oft extrem unregelmäßige Teilformen, die sich dann im letzten Schritt des Zusammensetzens zu einem regelmäßigen Objekt fügen. Außerdem erlauben die 60-Grad-Winkel Designs, bei denen mehrere Objekte gleichzeitig bewegt werden müssen. Das Puzzle „Rosebud“ von Stewart Coffin markiert einen Höhepunkt dieser Möglichkeit. Bei diesem Puzzle müssen 6 Teile gleichzeitig von einer Extremposition, an der sie sich nur an Ecken berühren, zum Zentrum des fertigen Objektes hin bewegt werden.
Entwirrspiele
Die Aufgabe bei Entwirrspielen ist meist, eine Metallschlaufe oder eine Fadenschlinge von einem Gegenstand zu lösen. Topologie spielt eine große Rolle bei diesen Spielen. Einfache Vertreter dieser Kategorie sind noch durch zufälliges Ausprobieren zu lösen. Komplexere Varianten erfordern wiederholende Lösungsmuster, die selbst bei Kenntnis der Komplettlösung einen verhältnismäßig hohen Zeitanspruch mit sich bringen.
Vier Vexiere aus Draht
Ein einfaches Entwirrpuzzle: Entferne die Schnur mit den zwei Kugeln vom Drahtgebilde!
Ineinandergreifendes lineares Ringpuzzle analog den chinesischen Ringen. Exponentielle Anzahl von Lösungsschritten entsprechend der Ringanzahl.
Im Gegensatz zu den chinesischen Ringen ist dieses verzweigte Geduldsspiel nicht linear.
Zu den Entwirrspielen gehören die Vexiere, bei denen zwei oder mehr ineinander verknotete Metalldrähte voneinander gelöst werden müssen. Auch diese Spiele hatten ihre erste weite Verbreitung am Ende des 19. Jahrhunderts mit dem allgemeinen Puzzle-Wahn. Eine große Anzahl von auch jetzt noch erhältlichen Vexieren haben ihren Ursprung in dieser Zeit.
Eine hervorstechende Art von Vexieren sind Ringpuzzles, zu denen auch die Chinesischen Ringe gehören. Bei diesen Spielen muss eine längliche Drahtschlaufe oder Fadenschlinge von einem Geflecht von ineinandergreifenden Ringen, Schlaufen und Drähten gelöst werden. Die Anzahl der notwendigen Schritte ist oft exponentiell zur Anzahl der ineinandergreifenden Hindernisse, wenn diese linear verlaufend verkettet sind. Zu den chinesischen Ringen gibt es die Geschichte, dass im Mittelalter Ritter ihren Frauen dieses Spiel geschenkt haben, damit denen die Zeit nicht lang wurde, während ihr Mann unterwegs war. Im Gegensatz zu den chinesischen Ringen gibt es auch Entwirrspiele mit ineinandergreifenden Hindernissen, die nicht linear verlaufen. Der Verlauf der Ringe verzweigt sich und wird wieder wie etwa bei James Dalgetys Devil's Halo zusammengeführt, wodurch die Komplexität der Lösung gesteigert wird. Die Verzweigungsidee kam 1970 auf. James Dalgetys Devil's Halo erhielt 1974 den London Design Centre Award.(Quelle: siehe Weblink)
Niels Bohr verwendete ein Entwirr-Puzzle namens Tangloids, um seinen Studenten die Eigenschaften des Spins anschaulich zu machen.
Faltspiele
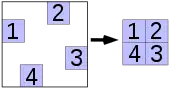
Bei diesen Puzzles muss ein Stück Papier mit Aufdrucken so gefaltet werden, dass ein bestimmtes Zielbild erreicht wird. Prinzipiell könnte man Rubiks Magic zu dieser Kategorie zählen. Ein anderes, besseres Beispiel ist im Bild dargestellt. Falte das quadratische Stück Papier so, dass die vier Quadrate mit den Nummern ohne Lücke nebeneinander liegen, ein Quadrat bilden. Dieses Puzzle ist schon ziemlich kompliziert.
Ein anderes Faltproblem hat wahrscheinlich jeder zu Hause: Faltprospekte, Stadtpläne und Packungsbeilagen. Trotz der sichtbaren Richtung an den Faltstellen ist es manchmal erstaunlich kompliziert, das Papier wieder so zusammenzulegen, wie es geliefert wurde.
Rätsel-Schlösser
Hierbei handelt es sich um Schlösser (oft in Form eines Vorhängeschlosses), die einen außergewöhnlichen Verschlussmechanismus haben. Aufgabe ist das Öffnen des Schlosses. Bei manchen Schlössern ist es dann aber schwieriger, den Ursprungszustand wiederherzustellen. Ein Beispiel für ein Puzzle-Schloss ist das Himitsu Bako.
Verwirrende Gefäße
Es handelt sich hier um Gefäße mit Tücken. Die Aufgabe besteht darin, aus dem Gefäß zu trinken oder einzuschenken, ohne die Flüssigkeit zu verschütten. Eine mögliche Konstruktion für ein Puzzle-Gefäß ist auf dem Bild zu sehen. Der Hals des Behälters enthält viele Löcher, die ein normales Einschenken nicht behindern, aber das Ausschenken unmöglich machen. Für den Puzzler unsichtbar ist eine Leitung durch den Griff entlang des oberen Randes des Gefäßes bis zur Tülle eingebaut. Wird jetzt mit einem Finger die Öffnung am oberen Ende des Griffes zugehalten, kann man durch Saugen an der Tülle Flüssigkeit trinken. Puzzlegefäße sind eine sehr alte Form von Spielen. Schon die Griechen und Phönizier stellten Gefäße her, die über eine Öffnung im Boden befüllt werden mussten. Im 9. Jahrhundert gab es in der Türkei eine Vielzahl verschiedener Gefäße, die in einem Buch ausführlich beschrieben wurden. Im 18. Jahrhundert stellten auch die Chinesen solche Trinkgefäße her.
Geschicklichkeitsspiele
Diese Kategorie umfasst keine Knobelspiele, da hier mehr die Geschicklichkeit und Ausdauer gefragt sind. Ziel ist es oft, kleine Kugeln durch vorsichtiges Kippen einer Schachtel mit transparentem Deckel in ein Loch zu manövrieren. Eine zeitgenössische Variante klassischer Kugellabyrinthe ist die sogenannte Perplexus-Kugel.
»Versuche die Kugel durch Kippen der Kiste entlang der Linie zum Ziel zu führen!«
»Auch hier muss eine Kugel in ein Ziel bugsiert werden!«
Spiele mit Bewegungsfolgen
Spiele dieser Kategorie erfordern die wiederholte Manipulation des Puzzles, um das Spiel in einen ganz bestimmten Zustand zu bringen. Bekannte Vertreter sind der Zauberwürfel und die Türme von Hanoi.
Zu dieser Kategorie gehören auch alle Schiebepuzzles, bei denen ein oder mehrere Steine an eine bestimmte Stelle geschoben werden sollen. Der bekannteste Vertreter ist das 15-Puzzle. Spiele wie Rushhour oder Sokoban gehören auch zu den Schiebespielen.
Drehpuzzle
Der Zauberwürfel hat einen ungeahnten Boom in dieser Kategorie bewirkt. Die Varianten an Objekten sind unüberschaubar. Neben Würfeln mit den Abmessungen von 2×2×2, 3×3×3, 4×4×4, 5×5×5, 6×6×6 und 7×7×7 gibt es unter anderem auch Tetraeder, Dodekaeder und verschiedene Formen von Zylindern. Die unterschiedliche Anordnung der Rotationsachsen erlaubt verschiedene Puzzles mit der gleichen Grundform. Weiterhin kann man durch Entfernen von Ebenen aus einem Würfel quaderförmige Spiele erhalten, die beim Manipulieren verschiedene unregelmäßige Formen annehmen (engl. shape shifting). Ein weiteres Spiel ist der Masterball.[2]
Das Bild zeigt einen anderen, weniger bekannten Vertreter dieser Gattung von Knobelspielen. Das Spiel ist auch noch so einfach, dass man es mit ein wenig Probieren und ein paar Notizen lösen kann, im Gegensatz zum Rubikwürfel, der schon zu schwer ist, um mit Probieren eine Lösung zu finden.
Einzelnachweise
Weblinks
- Gunnars Metallpuzzle und Geduldspiele Blog
- Diese Seite enthält Rezensionen und Informationen zu aktuellen Geduldspielen
- Webseite der Puzzleworld von Andreas Vahldieck
- Diese Seite enthält die gut bebilderte Vorstellung der Sammlung, Java-Applets zu verschiedenen Puzzles, Lösungen für verzweifelte Puzzlebesitzer und eine sehr umfangreiche Linkliste zu dem Thema Logikpuzzle und Vexiere.
- Webseite der Puzzlesammlung von John Rausch
- Diese Seite enthält neben einer gut bebilderten Vorstellung der Sammlung auch eine Seite mit Java-Applets von Schiebepuzzles. Außerdem sind auch die Bücher von Stewart Coffin, einem der wichtigsten Puzzle-Designer erhältlich.
- Puzzle Designs aufbereitet von ISHINO Keiichiro
- Diese Seite enthält eine riesige Sammlung von genauen Beschreibungen für Zusammensetz- und Verzahnenden Puzzles. Wer ein geschicktes Händchen besitzt, kann sich mit den hier vorgestellten Entwürfen eine eigene Sammlung erstellen.
- Devil's Halo im Puzzle Museum
- James Dalgetys Webpräsenz zum Puzzle Museum bietet eine Übersicht zu mittlerweile mehr als 5000 Geduldsspielen. Devil's Halo stellt einen modernen Vertreter von Entwirrspielen mit besonders hohem Schwierigkeitsgrad dar.
Literatur
- Jerry Slocum, Jack Botermans: Puzzles Old And New – How to make and solve them. Wellingborough 1987, ISBN 1-85336-018-X. (englisch)
- Jerry Slocum, Jack Botermans: Geduldspiele der Welt. Hugendubel, 1986, ISBN 3-88034-336-5.
- Stewart Coffin: The Puzzling World of Polyhedral Dissections. Oxford University Press, 1990, ISBN 0-19-853207-5.
- Stewart Coffin: Puzzle Craft 1985 Edition. Selbstverlag, Lincoln, MA 1985, OCLC 12869349.
- Stewart Coffin: Puzzle Craft 1992 Edition. (diese Bücher sind online erhältlich auf John Rauschs Web-Seite)
- Edward Hordern: Sliding Piece Puzzles (Recreations in Mathematics, No 4). Clarendon Press, 1987, ISBN 0-19-853204-0. (Hauptreferenz für Schiebepuzzles)
- Sophus Tromholt: Streichholzspiele : Denksport und Kurzweil. Spamer, Leipzig 1889 (Neuauflage: Hugendubel Verlag, München 1989, ISBN 3-88034-298-9).
- Rüdiger Thiele, Konrad Haase: Teufelsspiele. Urania Verlag, ISBN 3-332-00116-7.
- Pieter van Delft, Jack Botermans: Denkspiele der Welt. Hugendubel Verlag, ISBN 3-88034-087-0.
- Christoph Bandelow: Inside Rubik’s Cube and Beyond. Birkhäuser Verlag, ISBN 3-7643-3078-3.
- Tom Werneck: Zauberpyamide (teufelstonne – Tower – Trikki 4). Heyne Verlag, ISBN 3-453-41473-X.
- Tom Werneck: Die Zauberkugel. Heyne Verlag, ISBN 3-453-41505-1.
- Angus Lavery: Rubik’s CLOCK. Heyne Verlag, ISBN 3-453-03216-0.