Windchill

Der Windchill (engl.) bzw. die Windkühle (auch Windfrösteln) beschreibt den Unterschied zwischen der gemessenen Lufttemperatur und der gefühlten Temperatur in Abhängigkeit von der Windgeschwindigkeit. Er ist definiert für Temperaturen unterhalb von ca. 10 °C.

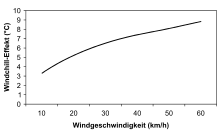
Gefühlte Temperaturdifferenz (Windchill-Faktor) bei 0 °C in Abhängigkeit vom Wind

Der Windchill-Effekt (engl. wind chill factor) wird durch die konvektive Abführung hautnaher und damit relativ warmer Luft und die damit einhergehende Erhöhung der Verdunstungsrate hervorgerufen. Die für den Phasenübergang des Wassers notwendige Energie wird dabei durch Wärmeleitung aus der Körperoberfläche abgezogen und kühlt diese dementsprechend ab. Der Wind hat daher die Wirkung, die Angleichung der Oberflächentemperatur des Körpers mit der Umgebungstemperatur der Luft zu beschleunigen, was Menschen als kühlend empfinden.

Während der Windchill vornehmlich für Temperaturen unterhalb der Behaglichkeit angewendet wird, ist für Temperaturen darüber der Hitzeindex aussagekräftiger.

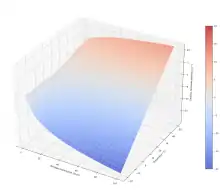
Gefühlte Temperatur in Abhängigkeit von der Windgeschwindigkeit

Quantifizierung – Größen des Windchill

Es gibt verschiedene Möglichkeiten, den Windchill-Effekt zu quantifizieren, so zum Beispiel über den Wärmeverlust pro betreffender Hautfläche oder über die Temperatur der Haut selbst. Diese haben sich bisher jedoch nicht gegen die derzeit vorherrschende Windchill-Temperatur (WCT) durchgesetzt oder wurden von ihr verdrängt.

Die WCT ist über die Lufttemperatur definiert, die bei schwachem Wind die gleiche Wärmeverlustrate pro dem Wind ausgesetzter Hautfläche verursachen würde wie die tatsächliche Lufttemperatur mit Windeinfluss. Diese Definition wurde aus Gründen der Verständlichkeit gewählt, da eine Temperatur von der breiten Öffentlichkeit besser verstanden wird als etwa die Angabe in Watt pro Quadratmetern. Es handelt sich also im eigentlichen Sinne nicht um eine Temperatur, sondern um ein Maß für die Wärmeverlustrate, das lediglich in Einheiten der Temperatur angegeben wird.

Dabei geht man von trockener Luft aus, berücksichtigt also nicht den bei niedrigen Temperaturen geringen Effekt der Luftfeuchtigkeit. Der hier verwandte „schwache Wind“ wird meist als „Windstille“ bezeichnet. Das kann jedoch zu Missverständnissen führen, da es sich normalerweise um eine Windgeschwindigkeit von 1,34 m/s (früher 1,79 m/s) beim Gehen handelt. Solange man als Bezug eine totale Windstille veranschlagt, ist die Windchill-Temperatur immer geringer als die tatsächlich messbare Temperatur.

Die Allgemeinverständlichkeit der WCT durch ihre Angabe in Temperatureinheiten führt leicht zu einem falschen Verständnis dessen, was die WCT eigentlich zum Ausdruck bringt. Es handelt sich dabei gerade nicht um die Temperatur, die ein Körper aufgrund des Windes annimmt. Bei einer gemessenen Temperatur von 5 °C und einer Windgeschwindigkeit von 55 km/h ergibt sich eine WCT von −1,6 °C (siehe unten), dennoch wird die Haut völlig unabhängig vom Wirkungszeitraum niemals Erfrierungen aufweisen. Die WCT ist nur ein Ausdruck dafür, um wie viel schneller sich die Temperatur der Haut an die gemessene Lufttemperatur von 5 °C annähert, als es ohne Wind der Fall wäre. Das erklärt auch, warum sich der Windchill nicht bei hohen Temperaturen zeigt, denn ein schnellerer Temperaturangleich spielt bei geringen Temperaturdifferenzen kaum eine Rolle.

Aktuelle Berechnung und Tabelle

Die seit November 2001 gültige empirische Formel in Form einer Zahlenwertgleichung zur Berechnung des Windchill mit metrischen Einheiten und einer in 10 Meter Höhe über dem Erdboden gemessenen Windgeschwindigkeit lautet:

\vartheta _{\mathrm {WCT} }=13{,}12+0{,}6215\cdot \vartheta _{\mathrm {a} }+(0{,}3965\cdot \vartheta _{\mathrm {a} }-11{,}37)\cdot v^{0{,}16}\!

ϑ_WCT – Windchill-Temperatur in Grad Celsius
ϑ_a – Lufttemperatur in Grad Celsius
v – Windgeschwindigkeit in Kilometern pro Stunde

Mit Einheiten des angloamerikanischen Maßsystems (für 33 Fuß Höhe über dem Erdboden):

\vartheta _{\mathrm {WCT} }=35{,}74+0{,}6215\cdot \vartheta _{\mathrm {a} }+(0{,}4275\cdot \vartheta _{\mathrm {a} }-35{,}75)\cdot v^{0,16}

ϑ_WCT – Windchill-Temperatur in Grad Fahrenheit
ϑ_a – Lufttemperatur in Grad Fahrenheit
v – Windgeschwindigkeit in Meilen pro Stunde (Landmeile)

Zu beachten ist dabei, dass sich die Formeln nicht auf eine komplette Windstille beziehen und man bei Windgeschwindigkeiten unter 1,34 m/s einen Wert erhält, der sich über dem der Lufttemperatur befinden kann. Das hat seine Ursache in der isolierenden Wirkung der hautnahen Luftschicht, die sich bei vollständiger Windstille erwärmt, ohne vom Wind weggetragen zu werden. Die dann wahrgenommene Lufttemperatur ist aufgrund dieser wärmeren Körperhülle höher als die tatsächliche Umgebungstemperatur in einiger Entfernung zur Hautoberfläche. Für derart niedrige Windgeschwindigkeiten ist die Formel allerdings nicht ausgelegt und die entsprechenden Ergebnisse sind unzuverlässig. In der Regel wird der Gültigkeitsbereich der Formel daher erst für Windgeschwindigkeiten über 5 km/h veranschlagt.

Die Ursprünge dieser Gleichungen, die Probleme in ihrer Umsetzung und Exaktheit sowie alternative Herangehensweisen werden in den folgenden Abschnitten dargestellt.

Windchill-Temperatur[1]
Windgeschwindigkeit	Lufttemperatur
00 km/h	10 °C	5 °C	0 °C	−5 °C	−10 °C	−15 °C	−20 °C	−30 °C	−40 °C	−50 °C
05 km/h	9,8	+4,1	−1,6	0−7,3	−12,9	−18,6	−24,3	−35,6	−47,0	−58,3
10 km/h	8,6	+2,7	−3,3	0−9,3	−15,3	−21,2	−27,2	−39,2	−51,1	−63,0
15 km/h	7,9	+1,7	−4,4	−10,6	−16,7	−22,9	−29,1	−41,4	−53,7	−66,1
20 km/h	7,4	+1,1	−5,2	−11,6	−17,9	−24,2	−30,5	−43,1	−55,7	−68,3
25 km/h	6,9	+0,5	−5,9	−12,3	−18,8	−25,2	−31,6	−44,5	−57,3	−70,2
30 km/h	6,6	+0,1	−6,5	−13,0	−19,5	−26,0	−32,6	−45,6	−58,7	−71,7
40 km/h	6,0	−0,7	−7,4	−14,1	−20,8	−27,4	−34,1	−47,5	−60,9	−74,2
50 km/h	5,5	−1,3	−8,1	−15,0	−21,8	−28,6	−35,4	−49,0	−62,7	−76,3
60 km/h	5,1	−1,8	−8,8	−15,7	−22,6	−29,5	−36,5	−50,3	−64,2	−78,0
Anmerkung: Bei blauen Feldern besteht die Möglichkeit, dass es innerhalb von 30 Minuten oder weniger zu Erfrierungen kommt. Erfrierungsgefahr besteht bei Erreichen einer Hauttemperatur von −4,8 °C, unterhalb der für etwa 5 % der Menschen Erfrierungen auftreten.

Bedeutung und Anwendung

Eine besondere Bedeutung besitzt der Windchill in kalten und windigen Regionen der Erde, insbesondere in Arktis, Antarktis und in den Hochgebirgen, also für Bergsteiger. Auch eine schnelle Bewegung des Menschen entspricht dabei einer hohen Windgeschwindigkeit, wovon bestimmte Wintersportarten betroffen sind. Eine große wirtschaftliche Bedeutung und somit politische Brisanz kommt dem Windchill daher in Wetterberichten der Wintersportgebiete zu, insofern er dort verwendet wird (was in Europa meist nicht der Fall ist). Der Effekt kann die Einsatzfähigkeit von Maschinen beeinträchtigen, insbesondere von Fahrzeugen. Er hat eine hohe Bedeutung für alles Leben in entsprechenden Extremklimaten und beeinflusst die Verbreitung von biologischen Arten in windoffenem Gelände.

Hauptanwendungsgebiet des Windchill in Form der WCT sind die USA und Kanada, weshalb die meisten Definitionen von dort oder dem National Weather Service und Environment and Climate Change Canada stammen. Beide nutzen derzeit vorgefertigte Tabellen zur Auswertung der Messdaten. Zusätzlich zu Anstrengungen in europäischen Staaten und Israel ergeben sich durch diese Vielfalt je nach verwendeter Fachliteratur oder Berechnungsverfahren, deren Aktualität und der eventuellen Anpassung an spezifische Bedingungen, teils erhebliche Unterschiede, sowohl in der grundsätzlichen Herangehensweise wie auch beim Ergebnis.

Geschichte

Einführung des Windchill

Die Entwicklung der ersten empirischen Formeln und Tabellen geht auf die Bemühungen der Streitkräfte der Vereinigten Staaten zurück, ihre Soldaten für die Härten der europäischen Winter des Zweiten Weltkrieges adäquat auszurüsten. Sie beauftragte die US-amerikanischen Polarforscher Paul Siple und Charles F. Passel, welche während der zweiten Antarktisexpedition Richard E. Byrds (1939–1941) im Winter des Jahres 1941 dazu ein Experiment durchführten. Ihre Messungen basierten dabei jedoch nicht auf einem Menschen, sondern auf einem mit 250 g Wasser gefüllten Kunststoffzylinder. Dieser bestand aus Celluloseacetat, war 14,9 cm lang, 5,7 cm im Durchmesser und hatte eine Dicke von 0,3 cm. Sie nutzten zwei Widerstandsthermometer zur Messung von Luft- und Wassertemperatur und ein Schalenkreuzanemometer zur Erfassung der Windgeschwindigkeit. Über die Zeitdauer des Gefriervorganges konnten sie mithilfe der bekannten Schmelzwärme des Wassers den Wärmeverlust des Zylinders in Kilokalorien pro Stunde (siehe Wärmestrom) und damit schließlich auch den Wärmeübergangskoeffizient in Kilokalorien pro Stunde, Quadratmeter und Grad Celsius ermitteln. Einflussgrößen waren dabei die dem Wind ausgesetzte Fläche des Zylinders sowie die Differenz aus dessen Temperatur (mit 0 °C veranschlagt) und der Lufttemperatur. Die Lufttemperaturen bewegten sich während ihrer Messungen im Bereich zwischen −56 °C und −9 °C, die Windgeschwindigkeiten von absoluter Windstille bis 12 m/s. Ihre ersten wirklichen Ergebnisse erhielten Siple und Passel durch eine grafische Interpolation eines Diagramms, in dem ihre gemessenen Windgeschwindigkeiten gegen die bestimmten Wärmeübergangskoeffizienten aufgetragen waren. Die resultierende Ausgleichsgerade dieser Interpolation (1.1) konnte nun leicht mit dem Wärmeverlust des Kunststoffzylinders verknüpft werden (1.2).

1.1)

\ \alpha =10{\sqrt {v}}+10{,}45-v

1.2)

\ \Phi =\alpha A(\vartheta _{\mathrm {O} }-\vartheta _{\mathrm {L} })

Auf Basis dieser Beziehung wurde der Wärmeverlust mit den Bedingungen der Windchill-Temperatur gleichgesetzt.

1.3)

\ \alpha A(\vartheta _{\mathrm {O} }-\vartheta _{\mathrm {L} })=\alpha _{0}A(\vartheta _{\mathrm {O} }-\vartheta _{\mathrm {WCT} })

Die einzelnen Formelzeichen stehen für folgende Größen:

α – Wärmeübergangskoeffizient mit Wind
α₀ – Wärmeübergangskoeffizient ohne Wind
v – Windgeschwindigkeit
Φ – Wärmestrom (Wärmemenge pro Zeit)
A – Flächeninhalt der Oberfläche
ϑ_O – Oberflächentemperatur
ϑ_L – Lufttemperatur
ϑ_WCT – Windchill-Temperatur

Für ϑ_O veranschlagten sie eine Temperatur der Haut von 33 °C und zur Bestimmung von α nach Formel 1.1 wurde eine Windgeschwindigkeit von 1,79 m/s genutzt. Die sich durch Umformungen schließlich ergebende empirische Gleichung für die Trockentemperatur in Grad Celsius und die Windgeschwindigkeit in km/h lautet:

1.4)

\ \vartheta _{\mathrm {WCT} }=33+(0{,}478+0{,}237\cdot {\sqrt {v}}-0{,}0124\cdot v)\cdot (\vartheta -33)

In der Formel werden nur die tatsächliche Temperatur und die Windgeschwindigkeit als Variablen verwendet. Sie ist im eigentlichen Sinne nur unter extremen Bedingungen, wie windstarken Bergkuppen mit niedriger Lufttemperatur gültig, denn zusätzlich zum Wind beeinflussen auch noch andere Parameter die gefühlte Temperatur, etwa die Luftfeuchtigkeit (siehe Humidex, Schwüle), Körpergröße und -gewicht, die Bekleidung, die Sonneneinstrahlung (Grad der Beschattung, Sonnenstand) und die Hautfeuchtigkeit.

In Kanada wurde nur die linke Seite von Gleichung 1.3 mit ansonsten identischen Annahmen genutzt. Man erhält dadurch über Umformungen den so genannten wind chill index (WCI) in Watt pro Quadratmeter, also den eigentlichen Wärmeverlust.

Der NWS veranschlagte für die WCT einen Schwellenwert von −29 °C, ab dem man von einer Gefährlichkeit des Windchill spricht. Dieser eher willkürliche Wert wird durch eine Vielzahl von Faktoren beeinflusst und sollte daher nur als ungefährer Richtwert gesehen werden. Als Beispiel würde ihn eine starke Sonneneinstrahlung erniedrigen.

Kritik an den Messungen von Siple und Passel

Die ursprünglichen Messungen weisen vielerlei Schwachstellen auf. So hat man zum Beispiel nur ein Thermometer zur Erfassung der Wassertemperatur genutzt, obwohl das Wasser im Kunststoffzylinder nur sehr ungleichmäßig gefriert. Das führt zu einem im Nachhinein nicht mehr ausgleichbaren Abweichen der Messwerte, die auf dem von Siple und Passel für ihre Interpolation genutzten Diagramm sehr weit gestreut lagen. Die Veranschlagung von 0 °C für den Kunststoffzylinder ignoriert zudem dessen thermischen Widerstand, der eine eigentlich niedrigere Temperatur bedingt. Hinzu kommt, dass die Probleme in Bezug auf eine Extrapolation von einem kleinen Kunststoffzylinder auf den Körper des Menschen nicht berücksichtigt wurden. Das gilt wiederum besonders für den thermischen Widerstand, der bei einer Hautoberfläche noch erheblich größer ist.

Das größte Problem ist jedoch wohl die Nutzung von 33 °C für die Temperatur der Haut, denn diese kann sich in einer kühlen Umgebung sehr schnell unter diesem Wert befinden. Ein noch zum Teil aktuelles Problem hängt mit der Messung der Windgeschwindigkeit zusammen. Diese wird als Eingangsgröße für die Gleichungen benötigt, meteorologisch standardisiert, jedoch in zehn Metern Höhe über dem Erdboden erfasst. In der Höhe eines Menschen, also zwischen dem Erdboden und rund zwei Metern, ist die Windgeschwindigkeit durch Reibungseffekte an Hindernissen jedoch in der Regel wesentlich geringer.

All diese Faktoren wirken zusammengefasst in Richtung einer Überbewertung des Windchill durch die Gleichung von Siple und Passel. Trotzdem haben es ihre Ergebnisse erstmals ermöglicht, einer breiten Öffentlichkeit den Windchill bewusst zu machen.

Weitere Entwicklung bis 2001

In den 1970er Jahren wurden diese Daten schließlich dem National Weather Service zur Verfügung gestellt und durch seine 1971 und 1984 erschienenen Arbeiten passte der australische Forscher Robert G. Steadman diese Formel auf einen bekleideten „Durchschnittsmenschen“ an. Das Ergebnis wurde vom National Bureau of Standards als offizielle Formel übernommen und vom National Weather Service in den USA ab 1973 angewandt. Es handelt sich dabei jedoch vielmehr um eine Reaktion der zuständigen Behörden auf die bereits in den 1960er und 1970er Jahren in den USA einsetzende Nutzung des Windchill durch einige Medienvertreter.

Steadman war es, der sich des Problems der Windgeschwindigkeitsmessung annahm. Er erstellte eine Formel, die für den Fall einer offenen Fläche die Windgeschwindigkeiten in Gesichtshöhe auf ungefähr zwei Drittel der Windgeschwindigkeiten in zehn Metern Höhe bestimmte. Noch größere Werte, alle mit einer Erhöhung der WCT verknüpft, zeigen sich dabei in Wäldern oder urbaner Umgebung. Da derartige Hindernisse in ihrer Beeinflussung der Windgeschwindigkeit schlecht zu kalkulieren sind, stellen sie weiterhin ein Problem dar. Ist der Einfluss der Umgebung nicht exakt feststellbar, sollte die standardisiert gemessene Windgeschwindigkeit dennoch grob korrigiert werden (solange die Korrektur nicht schon in der Gleichung enthalten ist).

Einen wesentlichen Fortschritt für die Genauigkeit von WCT/WCI ermöglichten die Arbeiten von Randall Osczevski im Jahr 1995. Er entwickelte ein Modell des menschlichen Kopfes und konnte so Messungen im Windkanal durchführen, wobei sich ähnliche Ergebnisse zu denen eines Zylinders ergaben. Maurice Bluestein und Zecher nutzen 1999 eine ähnliche Herangehensweise, jedoch nur mit einer theoretischen Analyse. Zylinder wählt man dabei deswegen, weil sie in der Fachliteratur der Wärmeleitung intensiv abgehandelt werden und folglich besser mathematisch zu modellieren sind. Osczevski ging in der Folge dazu über, nicht mehr den Kopf als Ganzes, sondern nur noch das Gesicht zu betrachten, da es dem Wind am stärksten ausgesetzt ist. Der Wärmeverlust bei schwachem Wind an dieser Stelle, der Frontseite der Versuchszylinder, erwies sich dabei als höher im Vergleich zu dessen Seiten. In Gleichung 1.3. hat das ein höheres α₀ zur Folge, was die WCT erhöht. Zusammen mit einer realistischen Temperatur für die Hautoberfläche ergaben sich höhere Temperaturen als bei Siple und Passle, Bluestein und Zecher und besonders für hohe Windgeschwindigkeiten auch Steadman. Ein Vergleich der verschiedenen Berechnungsmethoden wurde unter anderem von Quayle vorgenommen.

Besonders von Steadman wurden Anstrengung unternommen, weitere Faktoren wie die Strahlungsstärke und damit verbunden die Bewölkung einfließen zu lassen. Das führt jedoch zu einer zunehmenden Komplexität der Berechnungsgrundlage, wobei ein von Jahreszeit und Breitengrad abhängiger Faktor für die Sonneneinstrahlung noch einigermaßen gut umgesetzt werden könnte. Die Entwicklung eines Modells für den gesamten Körper mit Berücksichtigung von Metabolismus, Kleidung und verschiedener anderer Faktoren wurde unter anderem von Steadman vorgeschlagen, gestaltet sich jedoch schwierig. Einen Versuch in diese Richtung und damit der Angabe einer gefühlten Temperatur über große Intervalle, ohne dabei die Berechnungsgrundlage zu wechseln, stellt das Klima-Michel-Modell des Deutschen Wetterdienstes dar.

Heutige Berechnung ab 2001

Durch eine im Jahr 2000 von Seiten der kanadischen Verantwortlichen anberaumte Internetkonferenz wurde die Bestrebung forciert, eine grundlegende Reform der Windchill-Berechnungen durchzuführen. Eine Gruppe von Spezialisten, die Joint Action Group for Temperature Indices (JAG/TI) wurde damit beauftragt, eine Empfehlung für die WCT auszuarbeiten. Auch die International Society of Biometeorology (ISB) bildete eine Expertengruppe, um die internationale Übertragbarkeit verschiedener Lösungskonzepte zu prüfen. Im Jahr 2001 wurden zwei internationale Konferenzen durchgeführt, um die Probleme und Lösungsvorschläge bezüglich des Windchill zu thematisieren. Dabei standen die Fragen im Vordergrund, ob ein Temperaturindex für die gesamte Spanne des Wärmeübergangs entwickelt werden könne, ob dieser Index auf alle Klimate und Jahreszeiten anwendbar wäre, ob er für die Wettervorhersage und andere Verwendungen nutzbringend wäre und ob dieser Index unabhängig von individuellen Charakteristika sein würde, wie etwa der jeweiligen Kleidung.

Schließlich wurden Osczevski und Bluestein beauftragt, einen Kompromiss zwischen ihren ursprünglichen Arbeiten zu realisieren. Dafür wurden im Juni 2001 am Defence and Civil Institute of Environmental Medicine in Toronto Versuchsmessungen durchgeführt. Dabei wurden zwölf Personen in einem Windkanal unterschiedlichen Temperaturen und Windgeschwindigkeiten ausgesetzt, wodurch man Werte erhielt, die den thermischen Widerstand des Gesichtes besser berücksichtigten. Danach wurden die Methoden der Wärmeübertragung auf einen halben Zylinder angewandt, der das dem Wind zugekehrte Gesicht repräsentieren sollte. Die Bedingungen für Windstille wurden dabei auf einen Wert von 1,34 m/s reduziert, was einer realistischen Gehgeschwindigkeit von 4,8 km/h Rechnung tragen sollte. Durch eine Iteration mit fortschreitenden Abschätzungen der Hauttemperatur wurde auf dieser Basis der Wärmeverlust ermittelt und über einen Rückbezug auf die windstillen Bedingungen in eine WCT umgerechnet. Die Korrekturen für die Windgeschwindigkeitsmessung schloss man in diese Regressionsformeln ein, weshalb sie, wie angegeben, mit in 10 m Höhe gemessenen Windgeschwindigkeiten arbeiten.

Zukünftige Entwicklungen zielen vor allem auf die Berücksichtigung der Sonneneinstrahlung ab, es werden jedoch Verbesserungen in Bezug auf die Erfrierungsgefahr erwartet. Ein weiteres Forschungsfeld ist die Entwicklung eines Windchill unter Berücksichtigung des Einflusses von Nässe, was besonders für marine Umgebungen wichtig ist.

Kritik

Es gibt verschiedene Wege, den Effekt des Windchill quantitativ zu bestimmen. Meist werden einfache Näherungsformeln mit stark eingeschränkter Gültigkeit, vorgefertigte Tabellen oder auch Nomogramme verwendet. Allen Methoden ist jedoch gemein, dass der durch sie bestimmte Wert idealerweise nur unter Berücksichtigung seines Zustandekommens verwendet werden sollte, denn weder ergeben die verschiedenen Berechnungsmethoden einheitliche Ergebnisse, noch muss der berechnete Wert viel mit der Realität des konkreten Einzelfalles zu tun haben.

Allen Anstrengungen zum Trotz kann der Windchill nicht allgemeingültige Aussagen über das subjektive Temperaturempfinden eines Individuums treffen, da sich dieses schon per Definition der Allgemeingültigkeit entzieht. Was der Windchill letztendlich an Aussagen über dieses Temperaturempfinden treffen kann, hängt von einer Vielzahl von Faktoren ab. Die Annahmen, die in die Rechnungen einfließen, stellen zwar gute Mittelwerte dar, sind jedoch unzutreffend, wenn man in einer konkreten Situation von diesen Mittelwerten abweicht. Die Geschwindigkeit, mit der man geht oder fährt und die den Wind beeinflussende Umgebung, in der man sich bewegt, sind im Regelfall andere als jene, die für den Windchill veranschlagt wurden. Das Tragen einer großen Brille, ein umfangreicher Bartwuchs oder die Nutzung einer isolierenden Creme beeinflussen die Reaktion der Haut auf den Wind sehr stark, ebenso die Eigenheiten der körpereigenen Thermoregulation, die sich von Mensch zu Mensch stark unterscheiden. Ein Mensch mit großem Körpergewicht im Vergleich zur Körperoberfläche weist dabei geringere Hauttemperaturen auf, als eine schmächtige Person, die dafür aber auch leichter auskühlt (Hypothermie). Dazu kommt die unterschiedliche Akklimatisierung und auch genetische Adaption, was ein Vergleich zwischen dem Temperaturempfinden eines Mitteleuropäers und eines Eskimos bei −20 °C Außentemperatur illustriert.

Ein weiteres Problem ist, dass stillschweigend Meereshöhe vorausgesetzt wird, obwohl im Hochgebirge in großen Höhen, z. B. auf dem Gipfel des Kibo, die Luft nicht einmal die Hälfte der Dichte auf Meereshöhe hat. Dadurch ist die Wärmekapazität der Luft und die Wärmeleitung durch Konvektion entsprechend reduziert und der Windchill viel schwächer.

Der Windchill-Effekt wird häufig fälschlicherweise mit dem Begriff „gefühlte Temperatur“ gleichgesetzt. Das ist insofern irreführend, da auch bei hochsommerlichen Temperaturen Wind dazu führt, dass die Temperatur als niedriger empfunden wird. Hohe Luftfeuchtigkeit dagegen bewirkt bei niedrigen Temperaturen, dass die Temperatur kühler empfunden wird als die tatsächliche Temperatur; bei sehr warmer Umgebung lässt hohe Luftfeuchtigkeit dagegen die Temperatur als noch höher empfinden.

Diese Faktoren beschränken die Aussagekraft des Windchill zwar stark, jedoch kann bei ihrer Kenntnis auch deren Zuverlässigkeit eingeschätzt und an den Einzelfall angepasst werden. Das ist jedoch auch nur dann möglich, wenn genaue Kenntnisse über die WCT und deren Zustandekommen vorliegen, was jedoch meist nicht der Fall ist. Der Nutzen des Windchill im Rahmen eines Wetterberichts für die breite Bevölkerung wird daher oft als gering eingeschätzt und in Unkenntnis des Zustandekommens können die oft sehr niedrigen „Temperaturen“ abschreckend wirken. Aufgrund dieser Faktoren wird der Windchill oft als nutzlose Größe erachtet, die gerade für Laien keinen Mehrwert zur Angabe von realer Lufttemperatur und Windgeschwindigkeit besitzt. Das ist auch einer der Gründe, weshalb der Windchill außerhalb Nordamerikas selten Verwendung findet.

Siehe auch

Literatur

Maurice Bluestein, Jack Zecher: A New Approach to an Accurate Wind Chill Factor. In: Bulletin of the American Meteorological Society. Band 80, 2010, S. 1893–1899, doi:10.1175/1520-0477(1999)080<1893:ANATAA>2.0.CO;2.
J. C. Dixon, M. J. Prior: Wind-chill indices, a review. In: Meteorological Magazine. Band 116, Nr. 1374, 1987, S. 1–17.
James R. Holton (Hrsg.), John Pyle (Hrsg.), Judith Curry (Hrsg.): Encyclopedia of Atmospheric Sciences. Academic Press, San Diego/London 2002, ISBN 0-12-227090-8
Randall J. Osczevski: Windward Cooling: An Overlooked Factor in the Calculation of Wind Chill. In: Bulletin of the American Meteorological Society. Band 81, 2010, S. 2975–2978, doi:10.1175/1520-0477(2000)081<2975:WCAOFI>2.3.CO;2.
P. A. Siple, C. F. Passel: Measurements of dry atmospheric cooling in sub-freezing temperatures. Reports on Scientific Results of the United States Antarctic Service Expedition, 1939–1941. In Proceedings of the American Philosophical Society 89, 1945, S. 177–199, Australian Geographer 5, 1946, doi:10.1080/00049184608702259
R. G. Steadmen: Indices of wind chill of clothed persons. In Journal of Applied Meteorology. 10, 1971, S. 674–683, doi:10.1175/1520-0450(1971)010<0674:IOWOCP>2.0.CO;2
R. G. Steadmen: Comments on „Wind chill errors“. In Bulletin of the American Meteorological Society. 9, 1995, S. 1628–1630
R. G. Quayle, R. G. Steadmen: The Steadmen wind chill: an improvement over present scales. In Weather and Forecasting,13, 1998, S. 1187–1193
D. P. Wyon: Wind-chill equations predicting whole-body heat loss for a range of typical civilian outdoor clothing ensembles. In Scandinavian Journal of Work, Environment and Health. 15 (supplement 1), S. 76–83

Weblinks

Commons: Windchill – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Windchill – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Windchill-Rechner
Windchill-Erklärung. Windchill-Erklärung.
Wind Chill Index. National Weather Service (NWS), abgerufen am 2. Juni 2010 (engl., Tabelle der Windchill-Temperaturen mit spezifischer Erfrierungszeitdauer).
Canada’s Wind Chill Index. Environment and Climate Change Canada (engl.)
Miguel Tremblay: Wind Chill and Humidex. 31. Mai 2003, abgerufen am 2. Juni 2010 (engl., Vortrag, Kritik an Windchill und Humidex).
Der Windchill-Effekt: Gefrorene Wellen. MyVideo, 22. Januar 2008, abgerufen am 2. Juni 2010 (Video).

Einzelnachweise

Gefühlte Temperatur (Memento vom 16. März 2016 im Internet Archive)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Gefühlte Temperatur (Memento vom 16. März 2016 im Internet Archive)