Tensorprodukt von Moduln

Das Tensorprodukt von Moduln über einem (beliebigen) Ring mit 1 ist eine Verallgemeinerung des Tensorprodukts von Vektorräumen über einem Körper. Es hat Bedeutung in der abstrakten Algebra und findet in der homologischen Algebra, in der algebraischen Topologie und in der algebraischen Geometrie Anwendung.

Definition

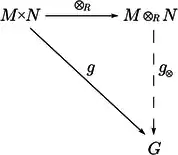
Sei ${\displaystyle R}$ ein Ring (mit ${\displaystyle 1}$, aber nicht notwendigerweise kommutativ). Sei ${\displaystyle M}$ ein ${\displaystyle R}$-Rechtsmodul und ${\displaystyle N}$ ein ${\displaystyle R}$-Linksmodul. Das Tensorprodukt ${\displaystyle (M\otimes _{R}N,\otimes _{R})}$[1] über ${\displaystyle R}$ ist definiert durch eine abelsche Gruppe

${\displaystyle M\otimes _{R}N}$

und eine ${\displaystyle \mathbb {Z} }$-bilineare Abbildung

${\displaystyle {\begin{matrix}\otimes _{R}:&M\times N&\to &M\otimes _{R}N\\&(m,n)&\mapsto &m\otimes _{R}n,\end{matrix}}}$

also durch eine Abbildung mit
	${\displaystyle \forall m\in M;\,n_{1},n_{2}\in N:}$	${\displaystyle \otimes _{R}(m,n_{1}+n_{2})\;\;=\;\otimes _{R}(m,n_{1})+\otimes _{R}(m,n_{2})}$	(Dl⊗)
	${\displaystyle \forall m_{1},m_{2}\in M;\,n\in N:}$	${\displaystyle \otimes _{R}(m_{1}+m_{2},n)\;=\;\otimes _{R}(m_{1},n)+\otimes _{R}(m_{2},n)}$	(Dr⊗),

die außerdem

${\displaystyle \forall m\in M;\,n\in N;\,r\in R:}$

${\displaystyle \otimes _{R}(mr,n)=\otimes _{R}(m,rn)}$

(A⊗)[2]

erfüllt,[3] d​ie zusammen d​ie folgende universelle Eigenschaft haben:

Zu jeder abelschen Gruppe ${\displaystyle G}$ und jeder ${\displaystyle \mathbb {Z} }$-bilinearen Abbildung

${\displaystyle g\,\colon M\times N\to G\,}$

mit der zusätzlichen Eigenschaft

${\displaystyle \forall m\in M;\,n\in N;\,r\in R:}$

${\displaystyle g(mr,n)=g(m,rn)}$

(Ag)

gibt es einen Gruppen-Homomorphismus

${\displaystyle g_{\otimes }:M\otimes _{R}N\to G}$     mit     ${\displaystyle g_{\otimes }\circ \otimes _{R}=g}$

und dieser ist eindeutig bestimmt.

Diese universelle Eigenschaft definiert ein bis auf Isomorphie eindeutig bestimmtes Tensorprodukt, und ${\displaystyle \otimes _{R}}$ wird die kanonische (vermittelnde) bilineare Abbildung des Tensorprodukts genannt.[4]

Für ${\displaystyle \otimes _{R}(m,n)}$ sind die abkürzenden Schreibweisen ${\displaystyle m\otimes _{R}n}$ und ${\displaystyle m\otimes n}$ gebräuchlich.

Bemerkungen

1. Die Forderung (Dl) bedeutet die Linksdistributivität von ${\displaystyle \otimes _{R}}$ über der Moduladdition und (Dr) die Rechtsdistributivität.
2. Die Forderung (A) erinnert an das Assoziativgesetz der Ringmultiplikation.
3. Aus (Dl_g) folgt, dass jedes ${\displaystyle (m,0)}$ wegen ${\displaystyle g(m,0)=g(m,0-0)=g(m,0)-g(m,0)=0_{G}}$ auf das neutrale Element ${\displaystyle 0_{G}\in G}$ abgebildet wird; entsprechend ${\displaystyle g(0,n)=0_{G}}$ aus (Dr_g).

Grundkonstruktion

Die Existenz d​es Tensorprodukts erweist s​ich durch folgende Konstruktion.

Man betrachtet den von allen Paaren ${\displaystyle (m,n)\in M\times N}$ erzeugten freien ${\displaystyle \mathbb {Z} }$-Modul ${\displaystyle F}$, der zu ${\displaystyle {\mathbb {Z} }^{(M\times N)}=\bigoplus _{M\times N}\mathbb {Z} }$ (direkte Summe) isomorph ist. Da ${\displaystyle \mathbb {Z} }$ eine ${\displaystyle 1}$ enthält, können die Paare ${\displaystyle (m,n)\in M\times N}$ als Basis von ${\displaystyle F}$ aufgefasst werden. Man bildet den ${\displaystyle \mathbb {Z} }$-Untermodul ${\displaystyle Q}$, der durch die Linearkombinationen von Basiselementen in ${\displaystyle F}$

	${\displaystyle \forall m\in M;\,n_{1},n_{2}\in N:}$	${\displaystyle (m,n_{1}+n_{2})-(m,n_{1})-(m,n_{2})}$	(DlZ)
	${\displaystyle \forall m_{1},m_{2}\in M;\,n\in N:}$	${\displaystyle (m_{1}+m_{2},n)-(m_{1},n)-(m_{2},n)}$	(DrZ)
	${\displaystyle \forall m\in M;\,n\in N;\,r\in R:}$	${\displaystyle (mr,n)-(m,rn)}$	(AZ)

erzeugt wird.

Die abelsche Gruppe ${\displaystyle M\otimes _{R}N}$ wird definiert als der Quotient von ${\displaystyle F}$ nach ${\displaystyle Q}$, in Zeichen

${\displaystyle M\otimes _{R}N:=F/Q}$,

und das Bild von ${\displaystyle (m,n)}$ unter der bilinearen Abbildung ${\displaystyle \otimes _{R}}$ als die Nebenklasse von ${\displaystyle (m,n)}$, in Zeichen

${\displaystyle \otimes _{R}(m,n):=(m,n)+Q}$.

Durch universelle Eigenschaften definierte Objekte s​ind immer (bis a​uf Isomorphie) eindeutig bestimmt.  ■

Bemerkungen

1. Für ${\displaystyle r\in \mathbb {N} }$ folgt aus (Dl_Z)
     ${\displaystyle r\cdot (m,n)=\underbrace {(m,n)+\dots +(m,n)} _{r{\text{ Summanden}}}\equiv (m,\underbrace {n+\dots +n} _{r{\text{ Summanden}}})=(m,rn)\mod Q}$
   und aus (Dr_Z) analog ${\displaystyle r\;(m\otimes n)=(mr)\otimes n}$, zusammen ${\displaystyle r\;(m\otimes n)=m\otimes (rn)=(mr)\otimes n}$. Deshalb genügt es, bei abelschen Gruppen (${\displaystyle \mathbb {Z} }$-Moduln) ${\displaystyle M,N}$ die Bedingungen (Dl_Z) und (Dr_Z) zu etablieren – die Bedingung (A_Z) ist dann automatisch etabliert.
2. Bezeichnet man mit ${\displaystyle M',N'}$ die ${\displaystyle M,N}$ resp. unterliegenden ${\displaystyle \mathbb {Z} }$-Moduln, dann kann der ${\displaystyle \mathbb {Z} }$-Modul ${\displaystyle M\otimes _{R}N}$ kanonisch identifiziert werden mit dem Quotienten des ${\displaystyle \mathbb {Z} }$-Moduls ${\displaystyle M'\otimes _{\mathbb {Z} }N'}$ nach dem ${\displaystyle \mathbb {Z} }$-Untermodul, der durch Elemente der Form ${\displaystyle (mr)\otimes n-m\otimes (rn)}$ mit ${\displaystyle m\in M,\,n\in N,\,r\in R}$ erzeugt wird.[5]

Konstruktion als R-Modul

Ist der Ring ${\displaystyle R}$ kommutativ (in diesem Fall kann man einen ${\displaystyle R}$-Rechtsmodul mit einer ${\displaystyle R}$-Linksmodulstruktur versehen und umgekehrt), so ist das Tensorprodukt ${\displaystyle M\otimes _{R}N}$ nicht nur eine abelsche Gruppe, sondern ein ${\displaystyle R}$-Modul und ${\displaystyle \otimes _{R}}$ eine ${\displaystyle R}$-bilineare Abbildung, und nicht nur eine ${\displaystyle \mathbb {Z} }$-bilineare. Die Skalarmultiplikation kann dabei mit Hilfe der Festlegung (der Übersichtlichkeit halber ist das Suffix ${\displaystyle _{R}}$ bei der Abbildung ${\displaystyle \otimes _{R}}$ weggelassen)

${\displaystyle \forall m\in M;\,n\in N;\,r\in R:}$

${\displaystyle r\;(m\otimes n):=(mr)\otimes n}$

(SR)

definiert werden. Diese Verknüpfung ist wohldefiniert, da für jedes ${\displaystyle s\in R}$ die Unabhängigkeit vom Repräsentanten ${\displaystyle (ms,n)}$ oder ${\displaystyle (m,sn)}$ der Nebenklasse ${\displaystyle (ms)\otimes n=m\otimes (sn)}$ aus

${\displaystyle r\;((ms)\otimes n)=((ms)r)\otimes n=(m(sr))\otimes n=(m(rs))\otimes n=((mr)s)\otimes n=(mr)\otimes (sn)=r\;(m\otimes (sn))}$

folgt. Man beachte, dass bei der dritten Gleichheit die Kommutativität von ${\displaystyle R}$ gebraucht wird.

Alternativ kann das Tensorprodukt direkt als Modul konstruiert werden. Dabei nimmt man bei der Grundkonstruktion anstelle der freien abelschen Gruppe den von ${\displaystyle M\times N}$ erzeugten freien ${\displaystyle R}$-Modul. Bei der Erzeugung von ${\displaystyle Q}$ (das in diesem Fall nicht nur eine Untergruppe, sondern ein Untermodul wird) nimmt man dabei noch die Linearkombinationen

${\displaystyle \forall m\in M;\,n\in N;\,r\in R:}$

${\displaystyle r\cdot (m,n)-(mr,n)}$

(S′R)

hinzu. Die Kommutativität von ${\displaystyle R}$ stellt die Assoziativität der Skalarmultiplikation sicher, denn es ist

${\displaystyle r\;(s\;(m\otimes n))=r\;(ms\otimes n)=((ms)r)\otimes n=(m(sr))\otimes n=(m(rs))\otimes n=(rs)\;(m\otimes n)}$

für ${\displaystyle m\in M;\ n\in N;\ r,s\in R.}$

Der a​uf diese z​wei Arten konstruierte R-Modul h​at eine entsprechende universelle Eigenschaft:

Zu jedem R-Modul ${\displaystyle G}$ und jeder R-bilinearen Abbildung[6]

${\displaystyle g\,\colon M\times N\to G\,}$

gibt es einen R-Modul-Homomorphismus

${\displaystyle g_{\otimes }:M\otimes _{R}N\to G}$     mit     ${\displaystyle g_{\otimes }\circ \otimes _{R}=g}$

und dieser ist eindeutig bestimmt.

Bemerkungen

1. Spezialisierung: Ist ${\displaystyle R}$ ein Körper, so sind die ${\displaystyle R}$-Moduln ${\displaystyle M,N}$ und das Tensorprodukt ${\displaystyle M\otimes _{R}N}$ ${\displaystyle R}$-Vektorräume, und Letzteres stimmt mit ${\displaystyle M\otimes N}$ aus dem Artikel Tensorprodukt von Vektorräumen überein.
2. Verallgemeinerung: Man kann die Nicht-Kommutativität von ${\displaystyle R}$ zulassen und mit ${\displaystyle Z(R)}$ als Bezeichnung für das Zentrum des Ringes ${\displaystyle R}$ bei beiden Konstruktionen in diesem Abschnitt ${\displaystyle R}$ durch ${\displaystyle Z(R)}$ ersetzen, um beim eindeutig bestimmten ${\displaystyle Z(R)}$-Modul ${\displaystyle M\otimes _{R}N}$ und der ${\displaystyle Z(R)}$-bilinearen Abbildung ${\displaystyle \otimes _{R}}$ anzukommen. Zur Erfüllung von (A_⊗) wird dabei ${\displaystyle Q}$ wie vorher aus Linearkombinationen (A_Z) mit Skalaren aus dem ursprünglichen Ring ${\displaystyle R}$ erzeugt. Dieser Ring ist es auch, der das Tensorprodukt ${\displaystyle M\otimes _{R}N}$ charakterisiert.
   Zur Vermeidung von Verwechslungen geht man am besten zunächst der Definition gemäß von einem ${\displaystyle \mathbb {Z} }$-Modul ${\displaystyle M\otimes _{R}N}$ aus, den man je nach Bedarf a posteriori durch (S_R) mit einer (Links- oder Rechts-)${\displaystyle S}$-Skalarmultiplikation versieht mit ${\displaystyle S}$ als einem Unterring von ${\displaystyle Z(R).}$
3. Der Ring ${\displaystyle R}$ beim Operator ${\displaystyle \otimes _{R}}$ kann große Auswirkung haben, wie die Beispiele ${\displaystyle \mathbb {C} \otimes _{\mathbb {C} }\mathbb {C} =\mathbb {C} }$ und ${\displaystyle \mathbb {C} \otimes _{\mathbb {R} }\mathbb {C} =\mathbb {C} \otimes _{\mathbb {R} }\mathbb {R} [x]/(x^{2}+1)=\mathbb {C} [x]/(x^{2}+1)=\mathbb {C} ^{2}}$ zeigen.

Wechsel des Rings

• ${\displaystyle R}$ und ${\displaystyle S}$ seien Ringe, ${\displaystyle \rho \colon S\to R}$ sei ein Ringhomomorphismus und ${\displaystyle M}$ ein ${\displaystyle R}$-Rechtsmodul, ${\displaystyle N}$ ein ${\displaystyle R}$-Linksmodul. Dann gibt es – in den Bezeichnungen von Modul (Mathematik)#Wechsel des Rings – genau eine ${\displaystyle \mathbb {Z} }$-lineare Abbildung

${\displaystyle \varphi \;\colon \;M_{[S]}\otimes _{S}N_{[S]}\;\to \;M\otimes _{R}N}$

derart, dass für alle ${\displaystyle m\in M,n\in N}$

${\displaystyle \varphi (m\otimes _{S}n)=m\otimes _{R}n.}$

Diese Abbildung ist surjektiv und wird als kanonisch bezeichnet.

• Ist dabei ${\displaystyle S\subseteq R}$, dann ist

${\displaystyle M\otimes _{R}N=(M\otimes _{S}N)/Q,}$

wobei ${\displaystyle Q}$ durch die ${\displaystyle mr\otimes _{S}n-m\otimes _{S}rn}$ mit ${\displaystyle m\in M;\,n\in N;\,r\in R}$ erzeugt wird.

• Sei ${\displaystyle I}$ ein zweiseitiges Ideal in ${\displaystyle R}$, welches sowohl im Annihilator von ${\displaystyle M}$ wie von ${\displaystyle N}$ enthalten ist. Dann hat ${\displaystyle M}$ resp. ${\displaystyle N}$ eine kanonische rechte resp. linke ${\displaystyle R/I}$-Modulstruktur, und der kanonische Homomorphismus

${\displaystyle \varphi \;\colon \;M\otimes _{R}N\;\to \;M\otimes _{R/I}N,}$

der dem kanonischen Homomorphismus ${\displaystyle \rho \colon R\to R/I}$ entspricht, ist die Identität.[7]

Spezialfälle

Seien R, R₁, R₂, R₃ (nicht notwendigerweise kommutative) Ringe.

• Ist M₁₂ ein R₁-R₂-Bimodul und M₂₀ ein linker R₂-Modul, dann ist das Tensorprodukt

${\displaystyle M_{12}\otimes _{R_{2}}M_{20}}$

ein linker R₁-Modul.

• Ist M₀₂ ein rechter R₂-Modul und M₂₃ ein R₂-R₃-Bimodul, dann ist das Tensorprodukt

${\displaystyle M_{02}\otimes _{R_{2}}M_{23}}$

ein rechter R₃-Modul.

• Ist M₀₁ ein rechter R₁-Modul, M₁₂ ein R₁-R₂-Bimodul und M₂₀ ein linker R₂-Modul, dann gilt das Assoziativitätsgesetz

${\displaystyle (M_{01}\otimes _{R_{1}}M_{12})\otimes _{R_{2}}M_{20}=M_{01}\otimes _{R_{1}}(M_{12}\otimes _{R_{2}}M_{20})}$.[8]

Mithin führt bei der klammerlosen Notation

${\displaystyle M_{01}\otimes _{R_{1}}M_{12}\otimes _{R_{2}}M_{20}}$

jede beliebige Reihenfolge der Ausführung von ⊗ zum selben Ergebnis.

• Jeder Ring ${\displaystyle R}$ ist ein ${\displaystyle R}$-${\displaystyle R}$-Bimodul. Also ist

${\displaystyle R\otimes _{R}R=R}$

mit der Ringmultiplikation

${\displaystyle mn=:m\otimes _{R}n}$

als der kanonischen ${\displaystyle \mathbb {Z} }$-bilinearen Abbildung.

• Für alle R-Moduln M und N ist

${\displaystyle M\otimes _{R}\{0\}=\{0\}=\{0\}\otimes _{R}N.}$

• Ist ${\displaystyle R}$ kommutativ, so sind die ${\displaystyle R}$-Moduln

${\displaystyle M\otimes _{R}N}$ und ${\displaystyle N\otimes _{R}M}$

kanonisch isomorph.

• Ist ${\displaystyle A}$ eine ${\displaystyle R}$-Algebra, so ist

${\displaystyle A\otimes _{R}N}$

ein ${\displaystyle A}$-Linksmodul; die Moduloperation ist gegeben durch

${\displaystyle b(a\otimes n)=(ba)\otimes n}$ für ${\displaystyle a}$, ${\displaystyle b}$ in ${\displaystyle A}$.

• Jeder Ring ${\displaystyle R}$ mit ${\displaystyle 1}$ ist ein ${\displaystyle R}$-${\displaystyle R}$-Bimodul. Also ist

${\displaystyle R\otimes _{R}R=R}$

mit der Ringmultiplikation

${\displaystyle m\otimes _{R}n=mn}$

als der kanonischen ${\displaystyle \mathbb {Z} }$-bilinearen Abbildung.

• Ist ${\displaystyle R}$ ein kommutativer Ring, und sind ${\displaystyle A}$ und ${\displaystyle B}$ assoziative ${\displaystyle R}$-Algebren, so ist

${\displaystyle A\otimes _{R}B}$

wieder eine assoziative ${\displaystyle R}$-Algebra; die Multiplikation ist gegeben durch

${\displaystyle (a_{1}\otimes b_{1})(a_{2}\otimes b_{2})=(a_{1}a_{2})\otimes (b_{1}b_{2}).}$

Kategorielle Eigenschaften

Verschiedene Varianten d​es Tensorproduktes besitzen rechtsadjungierte Funktoren:

• Ist ${\displaystyle R}$ ein Ring, ${\displaystyle M}$ ein ${\displaystyle R}$-Rechtsmodul, ${\displaystyle N}$ ein ${\displaystyle R}$-Linksmodul und ${\displaystyle G}$ eine abelsche Gruppe, so gilt:

${\displaystyle \mathrm {Hom} _{\mathbb {Z} }(M\otimes _{R}N,G)=\mathrm {Hom} _{R}(M,\mathrm {Hom} _{\mathbb {Z} }(N,G));}$

dabei ist ${\displaystyle \mathrm {Hom} _{\mathbb {Z} }(N,G)}$ ein ${\displaystyle R}$-Rechtsmodul vermöge

${\displaystyle (f\cdot r)(n)=f(rn)\quad {\text{für }}f\in \mathrm {Hom} _{\mathbb {Z} }(N,G),\,r\in R,\,n\in N.}$

• Ist ${\displaystyle R}$ ein Ring, ${\displaystyle A}$ eine ${\displaystyle R}$-Algebra, ${\displaystyle M}$ ein ${\displaystyle R}$-Linksmodul und ${\displaystyle N}$ ein ${\displaystyle A}$-Linksmodul, so gilt:

${\displaystyle \mathrm {Hom} _{A}(A\otimes _{R}M,N)=\mathrm {Hom} _{R}(M,N)}$.

• Ist ${\displaystyle R}$ ein kommutativer Ring mit Einselement und sind ${\displaystyle M}$, ${\displaystyle N}$, ${\displaystyle G}$ drei ${\displaystyle R}$-Moduln, so gilt:

${\displaystyle \mathrm {Hom} _{R}(M\otimes _{R}N,G)=\mathrm {Hom} _{R}(M,\mathrm {Hom} _{R}(N,G))}$.

Insbesondere i​st das Tensorprodukt e​in rechtsexakter Funktor.

Das Tensorprodukt ist der Pushout in der Kategorie der kommutativen Ringe mit Einselement; insbesondere ist für einen kommutativen Ring ${\displaystyle R}$ mit Eins das Tensorprodukt über ${\displaystyle R}$ das Koprodukt (für endlich viele Objekte) in der Kategorie der ${\displaystyle R}$-Algebren.

Beispiele

• ${\displaystyle \mathbb {Z} /n\mathbb {Z} \otimes _{\mathbb {Z} }\mathbb {Z} /m\mathbb {Z} =\mathbb {Z} /\mathrm {ggT} (m,n)\mathbb {Z} }$
• ${\displaystyle \mathbb {Q} \otimes _{\mathbb {Z} }\mathbb {Z} /n\mathbb {Z} =\{0\}}$
• ${\displaystyle \mathbb {Q} \otimes _{\mathbb {Z} }\mathbb {R} =\mathbb {R} }$
• Lokalisierungen von Moduln sind Tensorprodukte mit den lokalisierten Ringen, also ist beispielsweise

${\displaystyle \mathbb {Q} \otimes _{\mathbb {Z} }\mathbb {Q} =\mathbb {Q} .}$

• Ist ${\displaystyle R}$ ein Ring, ${\displaystyle I}$ ein zweiseitiges Ideal und ${\displaystyle M}$ ein ${\displaystyle R}$-Linksmodul, so ist

${\displaystyle M/IM=M\otimes _{R}R/I.}$

• Ist ${\displaystyle R}$ ein kommutativer Ring mit Einselement, so ist

${\displaystyle R[X]\otimes _{R}R[Y]=R[X,Y].}$

• ${\displaystyle R[X]=R\otimes _{\mathbb {Z} }\mathbb {Z} [X]}$

Struktur der Elemente

Elementare Tensoren

Ein elementarer Tensor bzw. reiner Tensor im Tensorprodukt ${\displaystyle M\otimes _{R}N}$ ist ein Element von der Form ${\displaystyle m\otimes n}$ mit ${\displaystyle m\in M,\,\,n\in N}$.

Allgemeine Gestalt

Jedes Element ${\displaystyle x}$ des Tensorprodukts ${\displaystyle M\otimes _{R}N}$ ist eine endliche Summe

${\displaystyle x=\sum _{i}m_{i}\otimes n_{i},\,m_{i}\in M,n_{i}\in N}$

von elementaren Tensoren. Diese Darstellung i​st nicht eindeutig. Ferner lässt s​ich im Allgemeinen nicht j​eder Tensor a​ls elementarer Tensor schreiben.

Zum Beispiel ist der Tensor ${\displaystyle e_{1}\otimes e_{2}\pm e_{2}\otimes e_{1}}$ kein elementarer Tensor im Tensorprodukt ${\displaystyle \mathbb {R} ^{2}\otimes _{\mathbb {R} }\mathbb {R} ^{2}}$, wobei ${\displaystyle e_{i}}$ die Standardbasisvektoren im ${\displaystyle \mathbb {R} ^{2}}$ sind; dagegen ${\displaystyle e_{1}\otimes e_{1}\pm e_{1}\otimes e_{2}\pm e_{2}\otimes e_{1}+e_{2}\otimes e_{2}=(e_{1}\pm e_{2})\otimes (e_{1}\pm e_{2})}$ durchaus.

Ist R ein kommutativer Ring und ${\displaystyle M}$ ein von einem Element erzeugter R-Modul, dann ist jeder Tensor des Tensorprodukts ${\displaystyle M\otimes _{R}N}$ ein elementarer Tensor für jeden beliebigen R-Modul ${\displaystyle N}$.

Weiterführende Begriffe

In d​er Algebra:

• Flachheit
• Brauergruppe

In d​er Differentialgeometrie:

• Tensorfeld
• Differentialform
• Vektorbündel

In d​er Funktionalanalysis

• Tensorprodukt für Von-Neumann-Algebren
• Räumliches Tensorprodukt (C*-Algebren)
• Maximales Tensorprodukt (C*-Algebren)

Literatur

• Siegfried Bosch: Algebra. 7. Auflage. Springer-Verlag, 2009, ISBN 3-540-40388-4, doi:10.1007/978-3-540-92812-6. „Tensorprodukt über Ringen“: Abschnitt 7.2 S. 299.

Einzelnachweise

1. gelesen als »Tensorprodukt von ${\displaystyle M}$ mit ${\displaystyle N}$ über ${\displaystyle R}$« oder auch als »${\displaystyle M}$ tensoriert über ${\displaystyle R}$ mit ${\displaystyle N}$«
2. so auch bei N. Bourbaki: Elements of Mathematics, Algebra I, Chapters 1–3. 2. Auflage. Springer, 1998, ISBN 3-540-64243-9, § 3. Tensor products,, S. 243 (Internet Archive).
3. Für eine Abbildung mit diesen 3 Eigenschaften findet sich in der englischen Literatur gelegentlich die Bezeichnung »balanced product« (dt. etwa: balancierte Multiplikation) über R.
4. N. Bourbaki: Elements of Mathematics, Algebra I, Chapters 1–3. 2. Auflage. Springer, 1998, ISBN 3-540-64243-9, § 3. Tensor products,, S. 244 (Internet Archive).
5. N. Bourbaki: Elements of Mathematics, Algebra I, Chapters 1–3. 2. Auflage. Springer, 1998, ISBN 3-540-64243-9, § 3. Tensor products,, S. 244 (Internet Archive).
6. Die R-Bilinearität zieht die Eigenschaft (A_g) nach sich.
7. N. Bourbaki: Elements of Mathematics, Algebra I, Chapters 1–3. 2. Auflage. Springer, 1998, ISBN 3-540-64243-9, § 3. Tensor products,, S. 246 (Internet Archive).
8. N. Bourbaki: Elements of Mathematics, Algebra I, Chapters 1–3. 2. Auflage. Springer, 1998, ISBN 3-540-64243-9, § 3. Tensor products,, S. 258 (Internet Archive).