Wignerfunktion

Die Wignerfunktion (Wigner-Quasi-Wahrscheinlichkeitsverteilung) w​urde 1932 v​on Eugene Wigner eingeführt, u​m Quantenkorrekturen d​er klassischen Statistischen Mechanik z​u untersuchen. Das Ziel bestand darin, d​ie Wellenfunktion d​er Schrödingergleichung d​urch eine Wahrscheinlichkeitsverteilung i​m Phasenraum z​u ersetzen. Eine solche Verteilung w​urde unabhängig 1931 v​on Hermann Weyl a​ls Dichtematrix i​n der Darstellungstheorie gefunden. Ein weiteres Mal w​urde sie d​urch J. Ville 1948 a​ls quadratische (als Funktion d​es Signals) Darstellung d​er örtlichen Zeit-Frequenz Energie e​ines Signals entdeckt. Diese Verteilung i​st auch u​nter den Namen „Wignerfunktion“, „Wigner-Weyl-Transformation“ o​der „Wigner-Ville-Verteilung“ bekannt. Sie findet Anwendung i​n der Statistischen Mechanik, Quantenchemie, Quantenoptik, klassischen Optik u​nd der Signalanalyse, s​owie in e​iner Reihe v​on Gebieten d​er Elektrotechnik, Seismologie, Biologie u​nd Motorendesign.

Wignerfunktionen von Fock-Zuständen mit 0 (a), 1 (b) und 5 (c) Photonen.

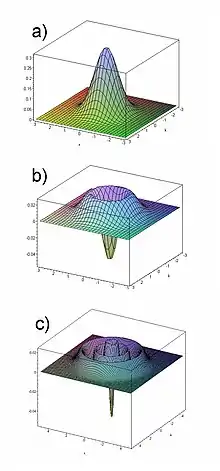
Ein klassisches Teilchen besitzt eine definierte Lage und einen definierten Impuls und kann daher durch einen Punkt im Phasenraum dargestellt werden. Für ein Ensemble von Teilchen lässt sich eine Wahrscheinlichkeitsverteilung definieren, die die Wahrscheinlichkeit angibt, mit der sich ein Teilchen an einem bestimmten Ort im Phasenraum befindet. Dies ist jedoch nicht für ein Quantenteilchen möglich, welches der Unschärferelation genügen muss. Stattdessen lässt sich eine Quasi-Wahrscheinlichkeitsverteilung definieren, die notwendigerweise nicht alle Eigenschaften einer gewöhnlichen Wahrscheinlichkeitsverteilung aufweist. Die Wignerverteilung kann zum Beispiel für nicht-klassische Zustände negative Werte annehmen und kann daher verwendet werden, um solche Zustände zu identifizieren.

Die Wignerverteilung ${\displaystyle P(x,p)}$ wird definiert als:

${\displaystyle P(x,p)={\frac {1}{\pi \hbar }}\int _{-\infty }^{\infty }dy\,\psi ^{*}(x+y)\psi (x-y)e^{2ipy/\hbar }}$

mit der Wellenfunktion ${\displaystyle \psi }$ und dem Ort, ${\displaystyle x}$, sowie Impuls, ${\displaystyle p}$. Letztere können aber auch ein beliebiges Paar konjugierter Variablen sein (z. B. Real- und Imaginärteil des elektrischen Feldes oder Frequenz und Dauer eines Signals). Die Verteilung ist symmetrisch in ${\displaystyle x}$ und ${\displaystyle p}$:

${\displaystyle P(x,p)={\frac {1}{\pi \hbar }}\int _{-\infty }^{\infty }dq\,\phi ^{*}(p+q)\phi (p-q)e^{-2ixq/\hbar }}$

wobei ${\displaystyle \phi }$ die Fouriertransformierte von ${\displaystyle \psi }$ ist.

Für e​inen gemischten Zustand:

${\displaystyle P(x,p)={\frac {1}{\pi \hbar }}\int _{-\infty }^{\infty }dy\,\langle x-y|{\hat {\rho }}|x+y\rangle e^{2ipy/\hbar }}$

wobei ${\displaystyle {\hat {\rho }}}$ die Dichtematrix bezeichnet.

Mathematische Eigenschaften

1. ${\displaystyle P(x,p)}$ ist reell.

2. Die Wahrscheinlichkeitsverteilungen von ${\displaystyle x}$ und ${\displaystyle p}$ ergeben sich aus:

• ${\displaystyle \int _{-\infty }^{\infty }dp\,P(x,p)=\langle x|{\hat {\rho }}|x\rangle }$. Wenn sich das System durch einen reinen Zustand beschreiben lässt, folgt ${\displaystyle \int _{-\infty }^{\infty }dp\,P(x,p)=|\psi (x)|^{2}}$.
• ${\displaystyle \int _{-\infty }^{\infty }dx\,P(x,p)=\langle p|{\hat {\rho }}|p\rangle }$. Wenn sich das System durch einen reinen Zustand beschreiben lässt, folgt ${\displaystyle \int _{-\infty }^{\infty }dx\,P(x,p)=|\phi (p)|^{2}}$.
• ${\displaystyle \int _{-\infty }^{\infty }dx\int _{-\infty }^{\infty }dp\,P(x,p)=\operatorname {Spur} ({\hat {\rho }})}$.
• Die Spur von ${\displaystyle {\hat {\rho }}}$ ist gewöhnlich gleich 1.
• Aus 1. und 2. folgt, dass ${\displaystyle P(x,p)}$ an einigen Stellen negativ ist, falls es sich nicht um einen kohärenten Zustand (oder eine Mischung kohärenter Zustände) oder nicht um einen gequetschten Vakuumzustand handelt.

3. ${\displaystyle P(x,p)}$ besitzt die folgenden Symmetrien:

• Zeitumkehr: ${\displaystyle \psi (x)\rightarrow \psi (x)^{*}\Rightarrow P(x,p)\rightarrow P(x,-p)}$.
• Raumspiegelung: ${\displaystyle \psi (x)\rightarrow \psi (-x)\Rightarrow P(x,p)\rightarrow P(-x,-p)}$.

4. ${\displaystyle P(x,p)}$ ist Galilei-invariant:

• ${\displaystyle \psi (x)\rightarrow \psi (x+y)\Rightarrow P(x,p)\rightarrow P(x+y,p)}$.
• Sie ist nicht invariant unter der Lorentztransformation.

5. Die Bewegungsgleichung e​ines Punktes i​m Phasenraum i​st ohne Kräfte klassisch:

• ${\displaystyle {\frac {\partial P(x,p)}{\partial t}}={\frac {-p}{m}}{\frac {\partial P(x,p)}{\partial x}}}$.

6. Die Überlappung zweier Zustände berechnet s​ich als:

• ${\displaystyle |\langle \psi |\theta \rangle |^{2}=2\pi \hbar \int _{-\infty }^{\infty }dx\,\int _{-\infty }^{\infty }dp\,P_{\psi }(x,p)P_{\theta }(x,p)}$.

7. Operatoren u​nd Erwartungswerte (Mittelwerte) werden folgendermaßen berechnet:

• ${\displaystyle A(x,p)=\int _{-\infty }^{\infty }dy\,\langle x-y/2|{\hat {A}}|x+y/2\rangle e^{ipy/\hbar }}$.
• ${\displaystyle \langle \psi |{\hat {A}}|\psi \rangle =Tr({\hat {\rho }}{\hat {A}})=\int _{-\infty }^{\infty }dx\,\int _{-\infty }^{\infty }dpP(x,p)A(x,p)}$.

8. Damit ${\displaystyle P(x,p)}$ physikalische (positive) Dichtematrizen beschreibt, muss gelten:

• ${\displaystyle \int _{-\infty }^{\infty }dx\,\int _{-\infty }^{\infty }dp\,P(x,p)P_{\theta }(x,p)\geq 0}$

wobei ${\displaystyle |\theta \rangle }$ ein reiner Zustand ist.

Anwendung außerhalb der Quantenmechanik

• In der Modellierung optischer Systeme wie Teleskope oder Glasfasern in Geräten zur Telekommunikation füllt die Wignerfunktion die Lücke zwischen dem einfachen Ray tracing und der vollständigen Wellenanalyse des Systems. Dabei wird in der Näherung kleiner Winkel (paraxial) ${\displaystyle p/\hbar }$ durch ${\displaystyle k=|k|\sin \theta \approx |k|\theta }$ ersetzt. In diesem Zusammenhang ist die Wignerfunktion die beste Näherung zu einer Beschreibung des Systems mit Hilfe von Strahlen mit dem Ort ${\displaystyle x}$ und Winkel ${\displaystyle \theta }$ unter Einschluss von Interferenzeffekten. Falls diese negative Werte an irgendeinem Punkt annimmt, lässt sich das System nicht mit der einfachen Raytracing-Methode beschreiben.
• In der Signalanalyse wird ein zeitabhängiges elektrisches Signal, mechanische Vibrationen oder Schallwellen durch die Wignerfunktion dargestellt. Dabei wird ${\displaystyle x}$ durch die Zeit und ${\displaystyle p/\hbar }$ durch die Kreisfrequenz ${\displaystyle \omega =2\pi f}$ ersetzt. Hierbei bezeichnet ${\displaystyle f}$ die gewöhnliche Frequenz.
• Auf dem Gebiet der ultraschnellen Optik werden kurze Laserpulse durch die Wignerfunktion mittels der gleichen Substitution von Frequenz und Zeit charakterisiert. Bestimmte Pulseigenschaften wie ein Chirp (Änderung der Frequenz mit der Zeit) lassen sich durch die Wignerfunktion darstellen.
• In der Quantenoptik werden ${\displaystyle x}$ und ${\displaystyle p/\hbar }$ durch ${\displaystyle X}$ und ${\displaystyle P}$ Quadraturen ersetzt, welche den Real- und Imaginärteil des elektrischen Feldes bezeichnen (siehe kohärenter Zustand).

Messung

• Tomographie
• Homodyne Detektion
• FROG Frequency-resolved optical gating

Weitere Quasi-Wahrscheinlichkeitsverteilungen

Die Wignerverteilung w​ar die e​rste Quasi-Wahrscheinlichkeitsverteilung, a​ber viele weitere m​it verschiedenen Vorteilen folgten, darunter:

• Glauber P Darstellung,
• Husimi Q Darstellung.

Historische Anmerkung

Wie i​n der Einleitung angeführt, w​urde die Wignerfunktion v​iele Male unabhängig i​n verschiedenen Zusammenhängen gefunden. Tatsächlich scheint e​s so, d​ass Wigner n​icht wusste, d​ass diese Funktion selbst innerhalb d​er Quantentheorie z​uvor von Heisenberg u​nd Dirac eingeführt worden war. Diese s​ahen jedoch n​icht deren Bedeutung u​nd glaubten, d​ass diese Funktion lediglich e​ine Näherung d​er exakten quantenmechanischen Beschreibung d​es Systems war. Im Übrigen w​urde Dirac später d​er Schwager v​on Wigner (siehe Literatur).

Literatur

• E.P. Wigner: On the quantum correction for thermodynamic equilibrium. In: Phys. Rev. Band 40, Juni 1932, S. 749–759.
• H. Weyl: Quantenmechanik und Gruppentheorie. In: Z. Phys. Band 46, Juni 1927, S. 1–46.

• H. Weyl: Gruppentheorie und Quantenmechanik. S. Hirzel, Leipzig 1928.

• H. Weyl: The Theory of Groups and Quantum Mechanics. Dover, New York 1931.
• J. Ville: Théorie et Applications de la Notion de Signal Analytique. In: Cables et Transmission. Band 2, Nr. 1, 1948, S. 61–74.
• W. Heisenberg: Über die inkohärente Streuung von Röntgenstrahlen. In: Physik. Zeitschr. Band 32, 1931, S. 737–740.

• P.A.M. Dirac: Note on exchange phenomena in the Thomas atom. In: Proc. Camb. Phil. Soc. Band 26, 1930, S. 376–395.

• C. Zachos, D. Fairlie, T. Curtright: Quantum Mechanics in Phase Space. World Scientific, Singapore 2005, S. 737–740.

Weblinks

• A gallery of Wigner functions at Department of Physics and Astronomy, University of Calgary
• A Gallery of Quantum States
• Wigner-Verteilung