Mutation (Knotentheorie)

In der Knotentheorie, einem Teilgebiet der Topologie bezeichnet man als Mutation eine Operation, die aus einem Knoten auf eine bestimmte Weise einen anderen Knoten macht.

Der Kinoshita–Terasaka-Knoten und der Conway-Knoten gehen durch Mutation auseinander hervor.

In der Regel unterscheidet sich ein Mutant vom ursprünglichen Knoten, jedoch haben beide Knoten viele Gemeinsamkeiten und insbesondere stimmen viele Knoteninvarianten überein. Es ist deshalb ein schwieriges knotentheoretisches Problem, Knoten von ihren Mutanten zu unterscheiden.

Der Begriff wurde in den 1960er Jahren von John Horton Conway eingeführt im Zusammenhang mit der Tangle-Notation zur Tabulierung von Knoten und Verschlingungen.

Definition

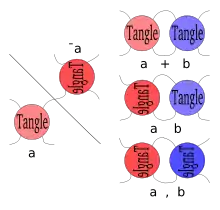
Tangle-Operationen Links: Ein Tangle a und sein Spiegelbild ⁻a. Oben rechts: Tangle-Addition a + b. Mitte rechts: Tangle-Produkt ab, äquivalent zu ⁻a + b. Unten rechts: Ramification a, b, äquivalent zu ⁻a + ⁻b

Man betrachtet eine Sphäre („Conway-Sphäre“), die den Knoten (nach geeigneter Verformung) in 4 symmetrisch liegenden Punkten schneidet. Der im Inneren der Sphäre liegende Teil des Knotens („Tangle“) wird um 180° gedreht oder so gekippt, dass paarweise je zwei Punkte vertauscht werden, und dann wieder mit dem außerhalb liegenden Teil des Knotens verbunden. Der so entstandene neue Knoten heißt Mutation des ursprünglichen Knotens.

Die Wirkung der Mutation auf die Knotenkomplemente lässt sich wie folgt beschreiben. Das Komplement des ursprünglichen Knotens wird entlang einer 4-fach gepunkteten Sphäre aufgeschnitten und anschließend mittels einer hyperelliptischen Involution der 4-fach gepunkteten Sphäre wieder verklebt. Das Ergebnis ist homöomorph zum Komplement des Mutanten.

Invarianten

Viele Knoteninvarianten stimmen für Knoten und ihre Mutanten überein: das Alexander-Polynom, das Jones-Polynom, das HOMFLY-Polynom, das gefärbte Jones-Polynom. Ruberman bewies 1987, dass die Mutation eines hyperbolischen Knotens wieder hyperbolisch ist und dasselbe hyperbolische Volumen hat.

Es ist deshalb schwierig, Knoten von ihren Mutanten zu unterscheiden. Eine Invariante, mit der manche Knoten von ihren Mutanten unterschieden werden können, ist Heegaard-Floer-Homologie. Die rechts abgebildeten Kinoshita-Terasaka- und Conway-Knoten unterscheiden sich durch ihr Seifert-Geschlecht.

Josh Greene hat bewiesen, dass für alternierende Knoten die folgenden drei Aussagen äquivalent sind:

L geht durch Mutation aus K hervor
$\Sigma (L)$ ist homöomorph zu $\Sigma (K)$
${\widehat {HF}}(\Sigma (L))={\widehat {HF}}(\Sigma (K))$

Hierbei bezeichnet $\Sigma (K)$ die entlang K verzweigte 2-fache Überlagerung der 3-Sphäre und ${\widehat {HF}}$ die Heegaard-Floer-Homologie.

Literatur

John H. Conway „An enumeration of knots and links and some of their related properties“, 1970.
Daniel Ruberman: „Mutation and volumes of knots in S³“, Inventiones Mathematicae 90, no.1, 189–215 (1987).
Stephan M. Wehrli: „Contributions to Khovanov homology“, Dissertation Zürich (2007).
Alexander Stoimenow, Toshifumi Tanaka, „Mutation and the colored Jones polynomial“, Journal of Gökova Geometry & Topology 3, 44–78 (2009).
Joshua E. Greene, „Lattices, Graphs and Conway Mutation“, pdf
Hugh R. Morton, Peter R. Cromwell: Distinguishing mutants by knot polynomials. J. Knot Theory Ramifications 5 (1996), no. 2, 225–238. pdf

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.