Napiersche Rechenstäbchen
Napiersche Rechenstäbchen (nach John Napier, der diese in seinem 1617 erschienenen Werk Rabdologiae seu numeratio per virgulas libri duo beschreibt) sind Rechenstäbchen, mit denen Multiplikationen und Divisionen durchgeführt werden können. Sie werden auch Nepersche Stäbchen oder Neperianische Rechenstäblein genannt. Das Arithmeum in Bonn, das weltweit größte Museum zu Rechenmaschinen, stellt diese Rechenstäbchen zum Multiplizieren vor. Um 1905 produzierte die Firma Merkur Verlag Remig Rees in Wehingen (Württemberg) dieses Rechenhilfsmittel unter dem Namen „Theutometer“ auf einzelnen Kartonstreifen, einsetzbar für bis zu 18 Stellen.[1]

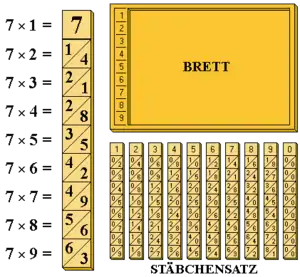
Die Stäbchen haben einen quadratischen Querschnitt. Auf jeder Längsseite eines Stäbchen ist spaltenweise eine Reihe des Einmaleins notiert. Beispielsweise stehen auf der rechts abgebildeten (Abb. 1) Seite eines Stäbchens die Vielfachen von 7, von 1×7 bis 9×7. Oben auf jeder Seite steht die jeweilige Grundzahl, im Beispiel also die 7.
Dabei ist jedes Zahlenfeld diagonal geteilt von links unten nach rechts oben. Im unteren rechten Dreieck steht die Einerstelle und im oberen linken Dreieck die Zehnerstelle des Produktes. Beispielsweise steht in der 4. Position des 7er-Stabes links oben 2 und rechts unten 8, entsprechend dem Produkt 4 × 7 = 28.
Die Stäbchen werden zur Multiplikation auf ein Tablett gelegt, an dessen linkem Rand die Zahlen 1 bis 9 untereinander aufgeführt sind. Die Stäbchen passen exakt in dieses Tablett hinein, so dass sie nicht vertikal verrutschen können.
Multiplikation
Die Multiplikation mit den Stäbchen soll an einem Beispiel erläutert werden.
Um das Produkt 7 × 46785399 zu berechnen, legt man die Stäbchen entsprechend den Ziffern des zweiten Faktors auf das Tablett, so dass ganz links ein Stäbchen der 4er Reihe, also mit der Ziffer 4 an oberster Stelle, liegt, rechts daneben ein Stäbchen aus der 6er Reihe, also mit der Ziffer 6 an oberster Stelle, und so weiter bis zum letzten, rechts liegenden Stäbchen mit der Ziffer 9 an oberster Stelle (siehe Abbildung 2).
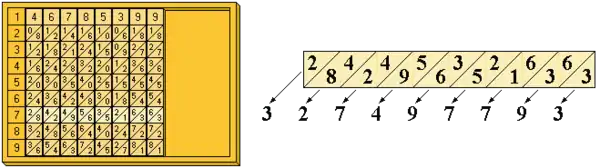
Das Ergebnis erhält man aus den Ziffern in der Zeile 7 (die in Abb. 2 weiß unterlegt ist). Von rechts nach links vorgehend, liest man jeweils die zwei Ziffern innerhalb eines aus zwei nebeneinanderliegenden Dreiecken gebildeten Parallelogramms ab, addiert sie und schreibt die Einerstelle des Ergebnisses auf. Ergibt sich bei der Addition eine Zahl größer als 9, wird die Zehnerstelle (1) in das nachfolgende, links daneben stehende Parallelogramm mit übernommen. So entsteht von rechts nach links das Ergebnis der Multiplikation, wobei rechts die Einerstelle steht, links daneben die Zehnerstelle und so weiter.
Das Ergebnis in unserem Beispiel ist demzufolge 7 × 46785399 = 327497793.
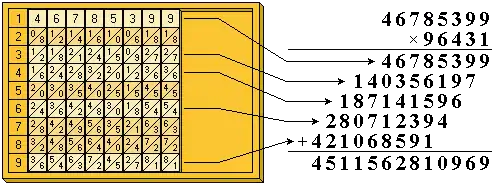

Auch Multiplikationen mit mehrstelligen Zahlen sind möglich. Um das vorige Beispiel weiterzuführen, soll das Produkt 96431 × 46785399 (mit dem gleichen zweiten Faktor) berechnet werden.
Dazu werden die Stäbchen ebenfalls wie in Abb. 2 gelegt. Damit werden dann nacheinander die Einzelmultiplikationen mit den Ziffern 1, 3, 4, 6, 9 (von rechts nach links) des ersten Faktors ausgeführt und die Ergebnisse untereinander, aber jeweils um eine Stelle nach links versetzt, aufgeschrieben, wie in Abb. 3 dargestellt.
Durch Addition der Einzelprodukte erhält man das gesuchte Gesamtergebnis der Multiplikation 96431 × 46785399 = 4511562810969.
Rechenmaschine
Nach einer Rekonstruktion hat Wilhelm Schickard die Stäbchen für seine – die erste – Rechenmaschine im Jahr 1623 verwendet, bei der die Addition der Teilprodukte mechanisch ausgeführt wurde.[2]
Einzelnachweise
- http://www.rechenwerkzeug.de/theutometer.htm
- Die erste „richtige“ Rechenmaschine. Abgerufen am 13. März 2019.