Luther-Bedingung
Die Luther-Bedingung ist sowohl in der Farbfotografie als auch in der Farbmesstechnik eine technische Forderung nach geeigneten Analysekomponenten, mit denen die menschliche Farbwahrnehmung bestmöglich simuliert werden soll. Benannt ist diese Forderung nach dem deutschen Kolloid- und Fotochemiker Robert Luther, der sie 1927 in seiner wissenschaftlichen Schrift Aus dem Gebiete der Farbreizmetrik erstmals formuliert hatte.
Formulierung der Luther-Bedingung
Robert Luther war einer der bedeutendsten Schüler des Chemie-Nobelpreis-Trägers Wilhelm Ostwald. Das eigentliche Forschungs- und Lehrgebiet Luthers war die Fotografie, doch wie sein Doktorvater Ostwald beschäftigte er sich auch mit der Farbenlehre. So wird nachvollziehbar, dass Luther wichtige Fortschritte auf dem Gebiet der Farbfotografie und Farbmesstechnik gelangen.
Einerseits entwickelte er ein Verfahren, mit dem später die spektrale Empfindlichkeit fotografischer Materialien standardisiert wurde. Andererseits wollte er den aus der Schwarzweißfotografie bekannten lichtempfindlichen Informationsträger Silberbromid für die Farbfotografie nutzbar machen, indem mit Hilfe einer gekoppelten Reaktion durch das Silber ein Farbstoff zerstört wird, sodass in einem zweiten Entwicklungsschritt an Stelle des konventionell entwickelten Silberbildes ein Farbstoffbild entsteht (Silber-Farbbleichverfahren).
Unmittelbares Ziel seiner Forschung war es, dünne Schichten zu schaffen, deren spektrale Filterwirkung die Belichtung und Entwicklung von Farbfilmen ermöglichen sollte. Somit war er einer der Pioniere des farbrichtigen Dreischichtenfarbfilms, wie er seit den 1930er Jahren fabriziert wird.
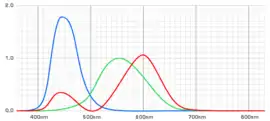
Für dieses Ziel benötigte er geeignete Farbfilter, die unter Berücksichtigung der Spektralempfindlichkeit der fotografischen Materialien die menschliche Farbwahrnehmung simulieren können. In Anlehnung an die Trichromasie – also das Farbensehen mit den rot-, grün- und blauempfindlichen Zapfen auf der Netzhaut des Auges – suchte er drei Lichtanalysefilter, deren spektrale Transmissionsgrade so verliefen, dass sie der Empfindlichkeit der Fotorezeptoren auf der Netzhaut gerecht wurden, zugleich aber auch die spektrale Empfindlichkeit des fotografischen Materials berücksichtigten. Ausgehend von den Spektralempfindlichkeiten der seinerzeit (1927) verwendeten Filmmaterialien, beschrieb er in seiner Schrift Aus dem Gebiete der Farbreizmetrik die Transmissionskurven der Filter, die für eine trichromatische Farbanalyse bzw. -messung geeignet sind.
Der spektrale Transmissionsgrad der Analysefilter, also ihr Lichtschwächungsfaktor in Abhängigkeit von der Wellenlänge , wird beschrieben durch die Kurven
- für die Rotorangefilter-Analyse,
- für die Grünfilter-Analyse und
- für die Blauviolettfilter-Analyse
- mit
- den Maßstabskonstanten für die Gesamtschwächungswirkung der Filter, also Koeffizienten zwischen 0 und 1;
- den drei spektralen Netzhautzapfen-Empfindlichkeitskurven (1931 benannt und standardisiert als CIE-Normspektralwertkurven);
- der spektralen Empfindlichkeitskurve eines geeigneten Lichtempfängers (Silberbromidschicht im Farbfilm, Sensor im Dreibereichsgerät).
Diese Formeln lassen sich in Worten wie folgt interpretieren: Nicht nur die Farbfilter, sondern auch der Lichtempfänger sind Analysekomponenten. Sie wirken immer zusammen, sodass sie immer aufeinander abgestimmt sein müssen.
In der Konsequenz stellte Luther somit zugleich eine allgemeine Forderung für die technische Simulation des Farbensehens auf.
Heutige Bedeutung der Luther-Bedingung
Anwendung in der Farbmesstechnik
Über die Farbfotografie hinaus gewann die 1927 formulierte Luther-Bedingung vor allem Bedeutung für die Farbmessung. Denn darin sind bereits die Grundlagen der Farbmesstechnik verankert. So wurde die Luther-Bedingung zuerst in den Dreibereichsmessgeräten (Kolorimeter) berücksichtigt, den in ihrem Aufbau einfachsten Farbmessgeräten. Kolorimeter besitzen drei Filter, deren spektraler Transmissionsgrad in Verbindung mit der Spektralempfindlichkeit der Sensoren exakt den Normspektralwertkurven (Tristimuluskurven) entsprechen. Heute werden diese Geräte nur noch für Messungen an Monitoren oder gefärbten Flüssigkeiten verwendet. In Auflichtmessgeräten wird zusätzlich die spektrale Verteilung der Messlichtquelle (mit näherungsweise einer Normlichtart) in die Berechnung der Messwerte einbezogen.[1][2] Bei Monitormessungen wird seit je her vorwiegend die Normlichtart D50 rechnerisch als Referenz simuliert.
Ca. seit dem Jahr 2000 erlebte diese Methode eine Renaissance mit der Verwendung von Videokameras als Kolorimeter. Die CCD- oder CMOS-Sensoren der Kamera liegen hierbei nicht hinter Filtern mit den üblichen spektralen Transmissionsgraden für Rot-, Grün- und Blau-Kanal. Vielmehr weisen die drei Filter die spektrale Charakteristik der Tristimuluskurven auf. Auf diese Weise wird die Videokamera zu einem schnellen und ziemlich zuverlässigen Detektor für geringste Farbunterschiede. Hauptanwendung ist das Erweitern von Inspektionssystemen an Druckmaschinen mit einer Funktion für das automatische Minimieren von Farbschwankungen.[3]
Auch moderne Farbmessgeräte, also Spektralfotometer und Spektraldensitometer, werden der Luther-Bedingung gerecht. Obwohl sie an Stelle des Dreibereichsfiltersatzes über einen Polychromator verfügen, der das Licht in alle Spektralfarben zerlegt, ist die Messanordnung Lichtquelle–Polychromator–(Vorschalt-/Sperrfilter–)Sensoren dennoch in der Lage, das menschliche Farbensehen zu simulieren. Dies ist möglich, indem aus dem gemessenen spektralen Remissionsgrad die entsprechenden Farbmaßzahlen berechnet werden.
Bewusstes Verletzen der Luther-Bedingung
Aber auch durch gezieltes Umgehen der Luther-Bedingung lassen sich nützliche Anwendungen schaffen. So soll bei der Multispektralfotografie eine naturgetreue Farbwiedergabe erzielt werden. Deshalb setzt diese Farbkamera-Anwendung nicht drei trichromatische Analysefilter vor dem Kamera-Sensor ein, sondern mindestens sieben auf einem vorgeschalteten Filterrad.[4] Indem sich die spektralen Transmissionsgrade dieser Filter möglichst stark überlappen, lässt sich durch Einzelmessung unter den jeweiligen Filterkanälen und deren anschließende rechnerische „Zusammenschaltung“ eine höhere Informationsdichte erzielen, vergleichbar mit der Informationsdichte in einem Spektraldensitometer. Primäres Ziel ist, einen größeren Originaldaten-Farbraum zu erzeugen, als das mit einer herkömmlichen RGB-Kamera möglich wäre. Auf der Syntheseseite, also im Offsetdruck, sollten dann natürlich mehr als die üblichen vier Druckfarben eingesetzt werden – etwa aus dem Hexachrome-System –, um einen deutlich größeren Farbraum auch im Druck zu erreichen.
Luther-Nyberg’scher Farbenkörper
Aus seiner Forderung nach den trichromatischen Filtern heraus entwickelte Luther in dem erwähnten Aufsatz Aus dem Gebiete der Farbreizmetrik außerdem die Idee eines Farbraums für Körperfarben (also Farbpigmente enthaltende Substanzen), den er als Farbenraum bezeichnete. Doch anders als in Ostwalds Farbenkörper, dem Ostwaldschen Doppelkegel (1918), erstellte Luther kein willkürlich kreisförmiges, sondern ein auf acht ausgewählten Optimalfarben basierendes Farbraummodell. Die Farbreiz-Messwertkurven X, Y, Z von Farbproben, die den Optimalfarben am nächsten kamen, überführte Luther in besser handhabbare Farbraumkoordinaten. Hierzu schuf er als Farbraumachsen die so genannten Farbmomente M₁und M₂ – quasi Drehmomente, die rechtwinkelig zueinander stehen und an der Helligkeitsachse A (Grauachse) des Farbkörpers angreifen. Den Farbmomenten liegt eine Zentrierung der Farbreiz-Kurven zu Grunde (gekennzeichnet als X', Y', Z'), um deren Helligkeit unabhängig von der spektralen Zusammensetzung des weißen Lichts (Lichtart) betrachten zu können; alle lichtartbezogenen X-, Y- und Z-Koordinaten nehmen dann den Wert 100 an.
Während M₁ und M₂ für die Farbart, also den Farbton mit einem bestimmten Sättigungsgrad stehen, gibt die senkrecht durch den Schnittpunkt von M₁ und M₂ laufende Raumachsenkoordinate den Hellbezugswert A an. So lässt sich im Farbraummodell für jedes Helligkeitsniveau A = 0 … 100 der ausgewählten Optimalfarben eine Schicht definieren, deren Kontur den maximal gesättigten Farbtönen entspricht. Welche Sättigung (Buntheit) ein konkreter Farbton (Buntton) aufweist, lässt sich aus den Farbmomenten M₁ und M₂ als Euklidischer Abstand des Farborts (von Luther als Buntmoment M bezeichnet) von der Farbraumachse A (wo M₁ = M₂ = 0 sind und aus der Formel herausfallen) berechnen:
Ein Jahr später beschrieb der schwedische Physiker Nikolaus D. Nyberg in seiner Schrift Zum Aufbau des Farbenkörpers im Raum aller Lichtempfindungen eine identische Farbraumkonstruktion, weshalb seitdem in der Fachliteratur vom Luther-Nyberg’schen Farbenkörper oder Luther-Nyberg-Farbkörper gesprochen wird.[5][6]
Literatur
- Luther, Robert: Aus dem Gebiete der Farbreizmetrik. Zeitschrift für technische Physik 8 (1927), Seiten 540–558
- Nyberg, N. D.: Zum Aufbau des Farbenkörpers im Raum aller Lichtempfindungen. Zeitschrift für Physik 52 (1928), Seiten 406–410
- Richter, Manfred: Einführung in die Farbmetrik. Walter de Gruyter – Sammlung Göschen, Band 2608, Berlin und New York 1976. ISBN 3-11-004751-9
Einzelnachweise
- Farbsensorik und Spektrale Technologien. TU Ilmenau, Fakultät für Informatik und Automatisierung, Fachgebiet Grafische Datenverarbeitung, abgerufen am 13. Dezember 2020.
- IDD: Farbmessgeräte. Praktische Farbmessung und Farbwissenschaften in der Papiertechnik. TU Darmstadt, S. 17–21, archiviert vom Original am 2014; abgerufen am 5. Februar 2010.
- Advanced Vision Technology Ltd: SpectraLink Online Press/Job color verification and management (Memento vom 29. Dezember 2009 im Internet Archive), abgerufen am 14. Februar 2010
- Forschungsgebiet – Multispektraltechnik: RWTH Aachen: Forschungsgebiet Multispektraltechnik (Multispektrale Farbbildaufnahme), abgerufen am 4. Februar 2010
- echo productions: (Memento vom 24. August 2010 im Internet Archive) R. Luther, N. D. Nyberg, abgerufen am 4. Februar 2010
- Eckhard Bendin: Entscheidende Grundlagen moderner Farbmessung. In: Dresdner UniversitätsJournal. 20. Jahrgang, Nr. 3, 17. Februar 2009, S. 8 (siehe Foto).