Logische Verknüpfung
Eine Logische Verknüpfung ist eine Operation der Booleschen Algebra. Mit Hilfe der logischen Verknüpfungen lassen sich in der Aussagenlogik und Schaltalgebra aus einfacheren Aussagen kompliziertere Aussagen zusammensetzen. Dabei muss der Wahrheitswert der zusammengesetzten Aussage durch die Wahrheitswerte der enthaltenen einfacheren Aussagen eindeutig bestimmt sein, beispielsweise durch eine Wahrheitstabelle (Wahrheitstafel). Eine Wahrheitstabelle ist die Definition einer logischen Verknüpfung. Mehrere Eingangssignale (1, 2, 3 oder mehr) werden mittels logischer Verknüpfung zu einem Ausgangssignal (auch 2 oder mehr Ausgangssignale sind möglich) zusammengesetzt. Die logische Verknüpfung definiert die Gesetzmäßigkeiten und logische Zusammenhänge zwischen Eingangssignal und Ausgangssignal.
Verknüpfungsarten
Logische Verknüpfungen werden auch Satzoperatoren genannt. Die Operatoren der logischen Verknüpfung werden Boolesche Operatoren genannt. Wichtige zweistellige logische Verknüpfungen sind Konjunktion, Disjunktion, Implikation und Äquivalenz. In der Digitaltechnik sind AND, OR, NOT, NOR und NAND die gängigsten logischen Grundschaltungen.
1. Kontradiktion
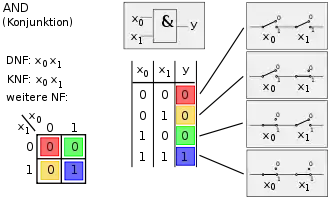
2. Konjunktion (AND-Verknüpfung)
3. Inhibition (AND-Verknüpfung mit Eingangsnegation)
4. Identität von a
5. Inhibition (AND-Verknüpfung mit Eingangsnegation)
6. Identität von b
7. Antivalenz (XOR-Verknüpfung)
8. Disjunktion (OR-Verknüpfung)
9. Peirce-Funktion (NOR-Verknüpfung)
10. Äquivalenz (NXOR-Verknüpfung)
11. Negation von b
12. Implikation aus b (OR-Verknüpfung mit Eingangsnegation)
13. Negation von a
14. Implikation aus a (OR-Verknüpfung mit Eingangsnegation)
15. Sheffer-Funktion (NAND-Verknüpfung)
16. Tautologie
In Analogie zum mathematischen Verknüpfungsbegriff spricht man von einstelligen (Bild 5) und zweistelligen (Bild 1 und 2) Verknüpfungen – je nachdem, wie viele Aussagen zusammengesetzt werden. Höherstellige Verknüpfungen (beispielsweise dreistellige Verknüpfung – Bilder) sind hier von untergeordneter Bedeutung, weil sie sich durch ein- und zweistellige Verknüpfungen ausdrücken lassen. Die Symbole, mit denen die logischen Verknüpfungen ausgedrückt werden, nennt man Junktoren.
Unter den einstelligen logischen Verknüpfungen gibt es nur eine nicht-triviale, nämlich die Negation.
Praktische Anwendung finden die logischen Verknüpfungen unter anderem als Suchoperatoren bei Datenbanken, Anfragen an Suchmaschinen und in der Digitaltechnik. Die praktische Realisierung von logischen Verknüpfungen in der Digitaltechnik erfolgt durch logische Schaltungen. Logische Verknüpfungen sind die Grundelemente der Digitaltechnik – unter anderem beim Schaltungsentwurf oder in der digitalen Steuerungstechnik.
Eine weitere praktische Anwendung der logischen Verknüpfungen besteht bei höheren Programmiersprachen, die meistens nur die Verknüpfungen AND, OR und NOT kennen, so dass die anderen logischen Verknüpfungen aus diesen drei Bausteinen konstruiert werden müssen. Programmiersprachen arbeiten nur mit zweistelligen logischen Ausdrücken. Mehrstellige logische Ausdrücke müssen ebenfalls durch Kombination mehrerer zweistelliger logischer Ausdrücke gebildet werden.
Die Definitionsmenge und die Zielmenge der logischen Verknüpfung sind jeweils W={w, f}, wobei ‚w‘ für wahr steht und ‚f‘ für falsch. Andere Schreibweisen sind:
- W={1, 0},
- W={WAHR, FALSCH},
- W={TRUE, FALSE}.
Zweistellige logische Verknüpfung
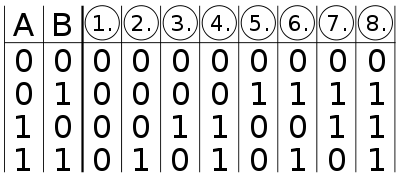
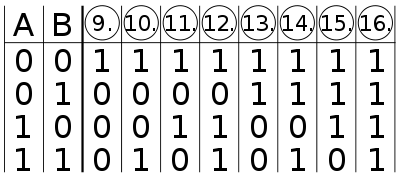
Wenn man zwei logische Variablen miteinander kombiniert, dann sind insgesamt 16 verschiedene Ergebnisse möglich. Eine Funktionstabelle mit zweistelligen logischen (Bild 1) Verknüpfungen (2 Eingänge) hat insgesamt vier Zeilen, also vier verschiedene Kombinationsmöglichkeiten der Eingangssignale. Folglich sind 16 verschiedene Ergebnisse möglich (24 = 16) – Bild 1 und 2. Jede der 16 möglichen zweiwertigen Verknüpfungen hat einen Namen. Es gibt 16 mögliche zweistellige Operatoren.
Die Spalten 1 bis 8 (Bild 1) stellen symmetrisch die Negationen der Spalten 9 bis 16 (Bild 2) dar. In den übrigen Bildern wird in der Mitte oben das logische Schaltsymbol nach EN 60617-12 dargestellt, rechts die elektrische Schaltung und in der Mitte unten die Wahrheitstabelle; links unten befindet sich das Karnaugh-Veitch-Diagramm, links oben sind die disjunktive Normalform, die konjunktive Normalform und ggf. eine weitere Normalform abgebildet.
In der Digitaltechnik wird die Funktion logischer Verknüpfungen durch Logikgatter realisiert; im Artikel Logikgatter sind auch die anderen gebräuchlichen Schaltsymbole dargestellt.
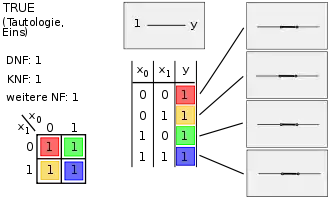 Bild 1, Spalte 16: TRUE (unabhängig von der Eingabe ist das Ergebnis immer „Eins“) – Tautologie – eine Tautologie wird in jedem Fall wahr. Es gibt unendlich viel Tautologien – beispielsweise: A OR NOT A. |
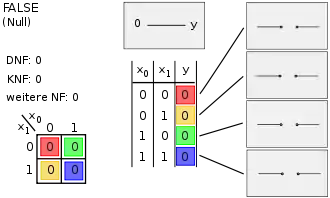 Bild 1, Spalte 1: FALSE (unabhängig von der Eingabe ist das Ergebnis immer Null) – Kontradiktion |
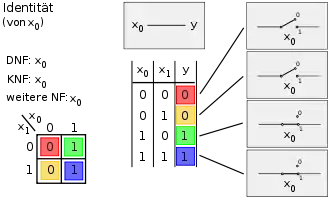 Bild 1, Spalte 4: Identität – Der Ausgang ist 1, wenn der Eingang A eine 1 ist |
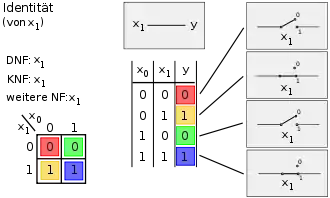 Bild 1, Spalte 6: Identität – Der Ausgang ist 1, wenn der Eingang B eine 1 ist |
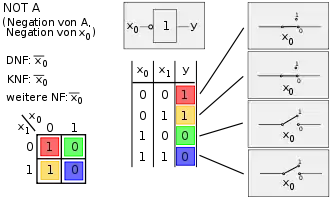 Bild 1, Spalte 13: Negation von A. |
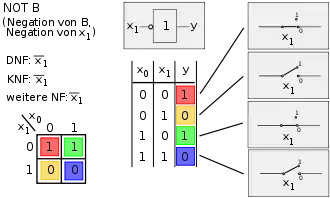 Bild 1, Spalte 11: Negation von B. |
 |
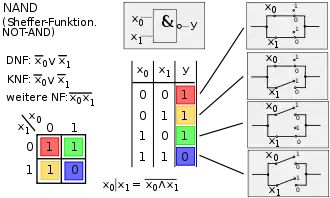 |
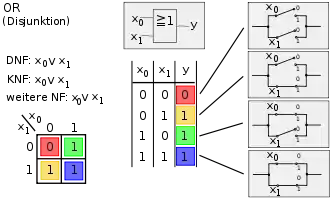 Bild 1, Spalte 8: OR (Disjunktion) – Der Ausgang ist 1, wenn ein oder zwei Eingänge 1 sind – Es muss mindestens 1 Teilausdruck wahr sein, damit der ganze Ausdruck wahr ist. |
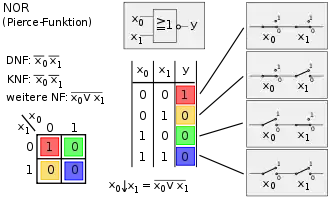 Bild 1, Spalte 9: NOR (Peirce-Funktion) – Kombination aus hintereinandergeschaltetem OR und NOT – Am Ausgang liegt 0 an, wenn an mindestens einem der Eingänge 1 anliegt. – NOR verhält sich umgekehrt zu OR. |
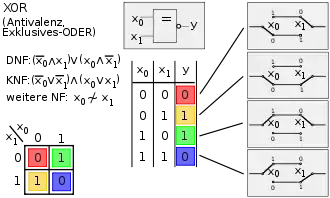 Bild 1, Spalte 7: XOR (Antivalenz, exklusives OR) – Der Ausgang ist 1, wenn die Eingänge unterschiedlich sind. – Wenn beide Eingänge unterschiedliche Logikzustände haben, dann wird am Ausgang 1 ausgegeben. – Nur wenn genau ein Eingang 1 ist, ist der Ausgang 1. |
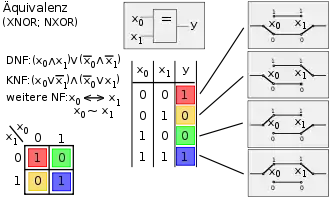 Bild 1, Spalte 10: XNOR (Äquivalenz) – XNOR ist das Gegenteil von XOR, also eine Kombination aus hintereinandergeschaltetem XOR und NOT. – Wenn beide Eingänge identische Logikzustände haben, dann wird am Ausgang 1 ausgegeben. |
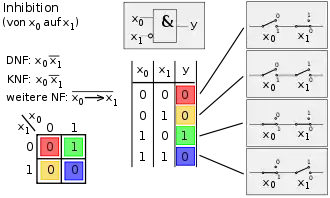 |
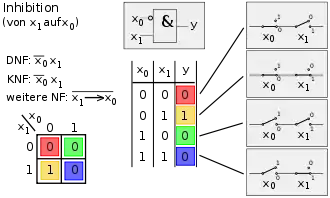 Bild 1, Spalte 5: Inhibition (Präsektion) (von B auf A) – Ein AND mit einem invertierten Eingang |
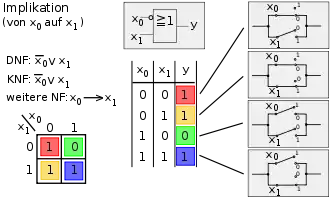 Bild 1, Spalte 14: Subjunktion (Implikation) (von A auf B) – Wenn A falsch (0) ist oder B wahr (1) ist, dann ist das Ergebnis wahr. |
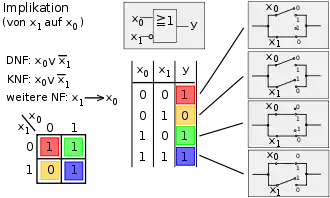 Bild 1, Spalte 12: Subjunktion (Replikation) (von B auf A) – Wenn B falsch (0) ist oder A wahr (1) ist, dann ist das Ergebnis wahr. |
- Die IEC 60617-12-Symbolik von XOR- und XNOR-Gatter ist vertauscht !!! XOR hat keine Negation am Ende der Verknüpfung.
Logische Verknüpfung in Computersprachen
Höhere Computersprachen, insbesondere C, C++, C#, Java und PHP, kennen die abgekürzte Auswertung, die sogenannte Kurzschlussauswertung, der logischen Operatoren für AND bzw. OR. Die abgekürzte Auswertung wird zur Optimierung der Laufzeit benutzt, sowie zur Vermeidung von Fehlern, die ohne die Abkürzung auftreten würden (z. B. x == 0 || a/x == 2). Der Operator && (AND) bezeichnet die abgekürzte Auswertung der Konjunktion. Wenn bereits die erste Eingangsvariable FALSCH ist, dann muss die zweite nicht mehr näher betrachtet werden, da das Ergebnis bereits bekannt ist – es muss FALSCH sein. Soll auf die abgekürzte Auswertung verzichtet werden, dann wird der Operator & verwendet. Analog wird für die Disjunktion der Operator || (OR) für die abgekürzte Auswertung und der Operator | für die nicht abgekürzte Auswertung der ODER-Funktion verwendet. Bei der ODER-Funktion steht das Endergebnis WAHR bereits fest, wenn die erste Eingangsvariable WAHR ist. Die weitere Auswertung der logischen Verknüpfung kann dann abgebrochen werden. Es gibt durchaus Gründe wie Seiteneffekte oder die beabsichtigte Ausnahmebehandlung, die die Existenz der Operatoren für die unbedingte Auswertung beider Operanden rechtfertigen.
In Visual Basic .NET werden Kurzschlussauswertungen durch die besonderen Schlüsselwörter AndAlso bzw. OrElse erzeugt.
Dreistellige logische Verknüpfung
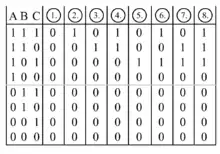
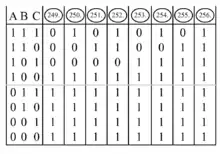
Bei drei Eingangsvariablen (A, B, C) gibt es 8 mögliche Kombinationen (die Tabelle hat 8 Zeilen). Es gibt 256 achtstellige Binärzahlen von 0000.0000 bis 1111.1111 (28 = 256). Folglich hat eine dreiwertige logische Verknüpfung 256 mögliche verschiedene Ergebnisse. Die wenigsten von ihnen haben einen allgemeinverbindlichen Namen. Die Abbildungen zeigen Anfang und Ende der 256 möglichen Kombinationen.
Obige Aussagen treffen nur für die binäre Logik zu, in der also eine Aussage nur den Wert 0 oder 1 annehmen kann, nicht jedoch für dreiwertige oder ähnliche mehrwertige Logiksysteme.
| ||||||||||||||||||||||||||||||||||||
| Operator:(A AND B AND NOT-C) OR (A AND NOT-B AND C) OR (NOT-A AND NOT-B AND C) |
Einstellige logische Verknüpfung
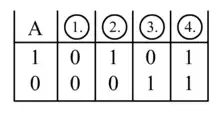
Die Abbildung zeigt alle vier Möglichkeiten einer einstelligen logischen Verknüpfung.
Mehrere logische Ausgänge
Weitere Variationsmöglichkeiten entstehen, wenn es statt eines Ergebnisses (bei logischen Digitalschaltungen: ein Ausgang) mehrere Ergebnisse (bei logischen Digitalschaltungen: mehrere Ausgänge) gibt – beispielsweise beim 1-aus-n-Decoder (2 Eingänge, 4 Ausgänge) oder Volladdierer (3 Eingänge, 2 Ausgänge).
Fuzzy-Logik
In der Fuzzy-Logik werden die logischen Operationen der Booleschen Algebra durch Fuzzy-Operationen ersetzt.
Literatur
- Klaus Beuth: Digitaltechnik – Elektronik 4. 12. Auflage. Vogel Fachbuchverlag, 2003, ISBN 3-8023-1958-3