Kornwachstum

Kornwachstum tritt in polykristallinen Festkörpern auf. Bei ausreichend hohen Temperaturen und sobald Kristallerholung und Rekristallisation vollständig stattgefunden haben, kann eine weitere Absenkung der inneren Energie nur noch über eine Verkleinerung der Korngrenzflächen erreicht werden. Dies geschieht durch Wachstum der größten und am günstigsten orientierten Kristallite ("Körner") auf Kosten kleinerer Vertreter. Dieser Vorgang kann sich idealerweise, aber praktisch eher selten, soweit fortsetzen, dass schließlich ein Einkristall entsteht.

Kornwachstumssimulation bei vorhandener Partikelverteilung. Die Simulation wurde mit einem Phasenfeldmodell unter Verwendung der Moelans-Funktion durchgeführt.

Der Begriff wird üblicherweise in der Metallkunde verwendet, kann sich aber auch auf keramische und mineralische Stoffe beziehen.

Bedeutung

Der überwiegende Anteil der Materialien weist bei Raumtemperatur den Hall-Petch-Effekt auf und erreicht daher bei kleineren Korngrößen eine höhere Streckgrenze. Bei hohen Temperaturen ist das Gegenteil der Fall, weil die offene und ungeordnete Struktur der Korngrenzen bewirkt, dass Leerstellen leichter und schneller entlang der Grenzen wandern können, was zu höherem Coble Creep führt (einer Art von Kriechen). Da Korngrenzen Regionen hoher Energie sind, bilden sie hervorragend Keimstellen für Ausscheidungen und andere Sekundärphasen: z. B. Mg-Si-Cu-Phasen in manchen Aluminiumlegierungen oder Martensit-Plättchen in Stahl. Je nach beteiligter zweiter Phase kann das positive oder negative Auswirkungen auf die makroskopischen Eigenschaften haben.

Regeln

Kornwachstum wurde lange Zeit vor allem durch die Untersuchung geschnittener, polierter und geätzter Proben unter dem optischen Mikroskop studiert. Obwohl dadurch ein breiter Bestand empirischen Anschauungsmaterials entstand, besonders auch im Hinblick auf Temperaturverläufe und Stoffzusammensetzungen, begrenzte die mangelnde Kenntnis der Kristallstruktur das Verständnis der grundsätzlichen physikalischen Prozesse. Dennoch konnte man folgende Grundeigenschaften des Kornwachstums definieren:

Kornwachstum entsteht durch Wanderung der Grenzflächen, nicht durch Koaleszenz (wie etwa bei Wassertropfen).
Die Wanderung der Grenzflächen verläuft diskontinuierlich, die Bewegungsrichtung kann dabei plötzlich wechseln.
Ein Korn kann ins andere wachsen, während es von der anderen Seite von einem weiteren verzehrt wird.
Die Verzehrrate steigt oft an, wenn ein Korn bereits beinahe aufgebraucht ist.
Eine bogenförmige Grenze wandert üblicherweise radial.
Sobald sich Korngrenzen einer einzelnen Phase in einem Winkel ≠ 120° treffen, wird das Korn aufgebraucht, das vom spitzeren Winkel getroffen wird, so dass alle Winkel 120° anstreben.

Normales und abnormales Wachstum

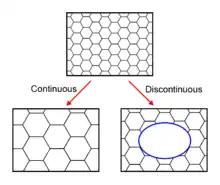
Unterschied zwischen kontinuierlichem und diskontinuierlichem Wachstum, bei dem einzelne Körner überproportional wachsen.

Gemeinsam mit Kristallerholung und Rekristallisation können Wachstumsphänomene in kontinuierliche und diskontinuierliche Prozesse eingeteilt werden. Bei Ersteren entsteht das Gefüge von Zustand A nach Zustand B gleichförmig, dadurch werden die Korngrößen höher. Im zweiten Fall finden die Veränderungen heterogen statt, so dass besondere transformierte als auch untransformierte Bereiche identifiziert werden können.

Diskontinuierliches Kornwachstum, auch sekundäre Rekristallisation genannt, ist durch einen Anteil an schnell wachsenden Körnern gekennzeichnet, die ihre Nachbarn schnell aufbrauchen; es tendiert zu einem resultierenden Gefüge, in dem wenige sehr große Körner dominieren. Damit das stattfindet, muss eine Teilmenge an Körnern einen Vorteil gegenüber den Wettbewerbern besitzen, also etwa hohe Grenzflächenenergie, hohe lokale Beweglichkeit der Grenzfläche (d. h. hohe Temperatur), ein günstiges Gefüge oder geringere Partikeldichte einer Sekundärphase, die die Korngrenzen "pinnt".

Treibende Kraft

Die Grenze zwischen einem Korn und seinem Nachbarn bildet einen Defekt der Kristallstruktur und geht deshalb mit einem gewissen Energiebetrag einher. Im Ergebnis entsteht eine thermodynamische Bestrebung, die Gesamtfläche der Korngrenzen zu reduzieren. Das geschieht beim Kornwachstum bei gleichzeitiger Reduktion der Gesamtanzahl von einzelnen Körnern.

Im Vergleich zu Phasenübergängen ist die erzielbare innere Energie beim Kornwachstum gering, daher findet es sehr viel langsamer statt und kann leicht durch Partikel oder lose Atome abgeschwächt werden.

Idealwachstum

Idealwachstum ist ein Sonderfall, bei dem lediglich die Reduktion der allgemeinen Grenzflächenenergie $\gamma$ wirkt. Dabei werden weitere Umgebungsbedingungen wie elastische Spannungen oder Temperaturgradienten vernachlässigt. Wenn man behaupten kann, dass die Wachstumsrate proportional zur wirkenden Kraft ist, und die wirkende Kraft proportional zur gesamten Grenzflächenenergie, kann gezeigt werden, dass die Zeit t, die erforderlich ist, um einen bestimmten Korndurchmesser zu erreichen, angenähert durch folgende Gleichung dargestellt werden kann:[1]

{\frac {dD}{dt}}=mK{\frac {\gamma }{D}}

wobei $D$ die Korngröße, $m$ die Mobilität der Korngrenze und $K$ der Proportionalitätsfaktor ist. Unter der Annahme, dass $K$ Zeitunabhängig ist, lässt sich die Gleichung vereinfachen zu:

D^{2}-{D_{0}}^{2}=kt\,\!

wobei D₀ die ursprüngliche Korngröße, D die endliche Korngröße und k eine temperaturabhängige Konstante darstellt, die exponentiell gebildet wird:

k=k_{0}\exp \left(-{\frac {Q}{RT}}\right)\,\!

wobei k₀ eine Konstante ist, T die absolute Temperatur und Q die Aktivierungsenergie für Grenzflächenverschiebungen. Theoretisch beträgt die Aktivierungsenergie für Grenzflächenverschiebungen so viel wie die für die Selbstdiffusion, aber das ist oft nicht zutreffend.

Allgemein gelten diese Gleichungen offenbar für hochreine Materialien, versagen aber bereits, wenn winzige Mengen gelöster Substanzen eingeführt werden.

Wachstumshemmende Faktoren

Wenn weitere Faktoren auftreten, die die Grenzbewegungen behindern, etwa das Zener-Pinning durch Kleinpartikel, kann sich die Korngröße auf einen viel geringeren Wert beschränken, als man normalerweise erwarten würde. Das ist ein fertigungstechnisch wichtiger Mechanismus, um die Erweichung von Materialien bei hohen Temperaturen zu verhindern. In Feinkornbaustahl übernehmen die Karbonitride der Mikrolegierungselementen Titan, Niob und Vanadium diese Rolle.

Siehe auch

Einzelnachweise

Gottstein, Günter: Materialwissenschaft und Werkstofftechnik Physikalische Grundlagen. 4., neu bearb. Aufl. 2014. Berlin, Heidelberg, ISBN 978-3-642-36603-1, S. 361.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Gottstein, Günter: Materialwissenschaft und Werkstofftechnik Physikalische Grundlagen. 4., neu bearb. Aufl. 2014. Berlin, Heidelberg, ISBN 978-3-642-36603-1, S. 361.