Phasenfeldmethode
Die Phasenfeldmethode ist ein Verfahren zur numerischen Simulation von Vorgängen, bei denen zwei oder mehr Phasen und die Grenzflächen zwischen ihnen, die Phasengrenzen, beschrieben werden sollen. Die Phasenfeldmethode wird eingesetzt, wenn berechnet werden soll, wie sich Strukturen und der Verlauf der Grenzflächen mit der Zeit ändern. Sie wurde insbesondere für Erstarrungsvorgänge angewandt, aber auch für viele andere Erscheinungen wie Musterbildung an der Grenzfläche zweier Flüssigkeiten oder für dynamische Vorgänge in der Bruchmechanik.
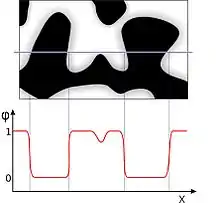
Zur Beschreibung des Gefüges bzw. der Verteilung der Phasen benutzt die Phasenfeldmethode eine Funktion, die kontinuierlich in Zeit und Raum ist, die Phasenfeldfunktion φ, auch Ordnungsparameter genannt. Beispielsweise kann sie bei der Beschreibung zweier Phasen Werte zwischen Null (erste Phase) und Eins (zweite Phase) annehmen.
Das Raumgebiet, in dem sich die Phasenfeldfunktion ändert, beschreibt die Phasengrenze, deren Position damit implizit gegeben ist, so dass sie nicht nochmals explizit verfolgt werden muss.[1] Das erleichtert die mathematische Beschreibung.
Die zeitliche Entwicklung der Phasenfeldfunktion wird mit Differentialgleichungen beschrieben, zusätzlich müssen die jeweiligen anderen Prozesse, z. B. Diffusion und Wärmeleitung, mit entsprechenden Gleichungen beschrieben werden, z. B. mit der Wärmeleitungsgleichung.
Vergleich mit anderen Methoden
Wie bei der Level-Set- und der Volume-of-Fluid-Methode wird die Phasenverteilung fest-flüssig durch eine charakteristische Funktion im Wertebereich [0,1] beschrieben. Diese Funktion wird zusätzlich zur physikalischen Beschreibung, beispielsweise der Temperatur, mitgeführt und gibt die prozentuale Verteilung der beiden Phasen flüssig-fest an.
Im Unterschied zur Levelset-Methode ist die Phasenfeldmethode inhärent, d. h. es existiert eine direkte Gebiets-Differentialgleichung zur Beschreibung der Interfacebewegung, die auf thermodynamischen Grundsätzen beruht. Sie ist daher nicht direkt für allgemeine chemische Diffusionsprozesse mit Oberflächendynamik oder andere Freiformaufgaben allgemeiner Stefan-Probleme einsetzbar.
Eine Modifikation der Phasenfeldmethode ist die Phasefield-Crystal-Methode, die eine anisotrope Beschreibung der atomaren Erstarrungsstruktur von mehrkomponentigen Legierungen ermöglicht, während das Phasenfeld eine mesoskopische Beschreibung der Erstarrung darstellt.
Anwendungen
Die Phasenfeldmethode eignet sich zur Simulation der dendritischen Erstarrung von Metallen. Hierbei können mehrfache Diffusionsgleichungen gekoppelt werden, um beispielsweise das Lösungsverhalten verschiedener Metalle bei der Erstarrung von Stahl zu berücksichtigen.
Mehrparametrische Weiterentwicklungen der Phasenfeldmethode erlauben die Simulation der eutektischen Erstarrung binärer Legierungen wie Titan-Eisen.
Weblinks
- Hermann-Josef Diepers: Direkte Mikroskopische Simulation der Erstarrungsmorphologie. ACCESS e.V. angegliedert an die RWTH Aachen, abgerufen am 2. Dezember 2014.
- Modellierung, Analysis und Numerik von lokalen und nichtlokalen Phasenfeldmodellen. Weierstraß-Institut für Angewandte Analysis und Stochastik WIAS, abgerufen am 2. Dezember 2014.
Literatur
- Nikolas Provatas und Ken Elder: Phase-Field Methods in Materials Science and Engineering. Wiley-VCH 2010, ISBN 978-3-527-40747-7.
Einzelnachweise
- Nele Moelans, Bart Blanpain, Patrick Wollants: An introduction to phase-field modeling of microstructure evolution. In: Calphad – Computer Coupling of Phase Diagrams and Thermochemistry. Band 32, Nr. 2, Juni 2008, S. 268–294, doi:10.1016/j.calphad.2007.11.003.