Koordinatenebene

Als Koordinatenebene bezeichnet m​an in d​er analytischen Geometrie e​ine von z​wei Einheitsvektoren aufgespannte Ursprungsebene. In z​wei Dimensionen entspricht d​ie Koordinatenebene d​er euklidischen Ebene u​nd damit d​er Grundfläche e​ines kartesischen Koordinatensystems. Im dreidimensionalen Raum g​ibt es d​rei Koordinatenebenen: d​ie xy-Ebene, d​ie xz-Ebene u​nd die yz-Ebene.

Die Koordinatenebene im zweidimensionalen Raum

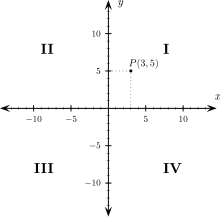
Analytische Geometrie

Bezeichnungen

Die drei Koordinatenebenen im dreidimensionalen Raum

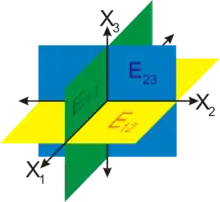
Im Folgenden seien die drei Koordinatenachsen des dreidimensionalen Raums ${\displaystyle \mathbb {R} ^{3}}$ mit ${\displaystyle x_{1}}$, ${\displaystyle x_{2}}$ und ${\displaystyle x_{3}}$ bezeichnet. Die drei Koordinatenebenen werden häufig mit den Buchstaben ${\displaystyle E}$ gekennzeichnet, der mit zwei Indizes versehen wird, die die beiden Einheitsvektoren angeben, von denen die Ebene aufgespannt wird:

• die ${\displaystyle x_{1}x_{2}}$-Ebene ${\displaystyle E_{12}}$ wird von den Vektoren ${\displaystyle {\vec {e}}_{1}}$ und ${\displaystyle {\vec {e}}_{2}}$ aufgespannt
• die ${\displaystyle x_{1}x_{3}}$-Ebene ${\displaystyle E_{13}}$ wird von den Vektoren ${\displaystyle {\vec {e}}_{1}}$ und ${\displaystyle {\vec {e}}_{3}}$ aufgespannt
• die ${\displaystyle x_{2}x_{3}}$-Ebene ${\displaystyle E_{23}}$ wird von den Vektoren ${\displaystyle {\vec {e}}_{2}}$ und ${\displaystyle {\vec {e}}_{3}}$ aufgespannt

Hierbei sind die drei Einheitsvektoren ${\displaystyle {\vec {e}}_{1}=(1,0,0)}$, ${\displaystyle {\vec {e}}_{2}=(0,1,0)}$ und ${\displaystyle {\vec {e}}_{3}=(0,0,1)}$. Durch die drei Koordinatenebenen wird der dreidimensionale Raum in acht Oktanten zerlegt. Der Schnitt zweier Koordinatenebenen ergibt eine Koordinatenachse, der Schnitt aller drei Koordinatenebenen den Koordinatenursprung.

Ebenengleichungen

Die d​rei Koordinatenebenen werden d​urch die folgenden Ebenengleichungen charakterisiert:

Koordinatenebene	Koordinatenform	Normalenform	Parameterform	Achsenabschnittsform
${\displaystyle E_{12}}$	${\displaystyle x_{3}=0}$	${\displaystyle {\vec {e}}_{3}\cdot {\vec {x}}=0}$	${\displaystyle {\vec {x}}=s\,{\vec {e}}_{1}+t\,{\vec {e}}_{2}}$	nicht definiert
${\displaystyle E_{13}}$	${\displaystyle x_{2}=0}$	${\displaystyle {\vec {e}}_{2}\cdot {\vec {x}}=0}$	${\displaystyle {\vec {x}}=s\,{\vec {e}}_{1}+t\,{\vec {e}}_{3}}$	nicht definiert
${\displaystyle E_{23}}$	${\displaystyle x_{1}=0}$	${\displaystyle {\vec {e}}_{1}\cdot {\vec {x}}=0}$	${\displaystyle {\vec {x}}=s\,{\vec {e}}_{2}+t\,{\vec {e}}_{3}}$	nicht definiert

Hierbei sind ${\displaystyle {\vec {x}}=(x_{1},x_{2},x_{3})\in \mathbb {R} ^{3}}$ ein Punkt der jeweiligen Ebene, ${\displaystyle {\vec {x}}\cdot {\vec {y}}}$ das Skalarprodukt der Vektoren ${\displaystyle {\vec {x}}}$ und ${\displaystyle {\vec {y}}}$ sowie ${\displaystyle s}$ und ${\displaystyle t}$ reelle Zahlen.

Darstellende Geometrie

In d​er darstellenden Geometrie entsprechen d​ie drei Koordinatenebenen häufig d​er Grundrissebene, d​er Aufrissebene u​nd der Kreuzrissebene.

Siehe auch: Normalprojektion

Synthetische Geometrie

In d​er synthetischen Geometrie w​ird eine affine o​der projektive Ebene, d​er als Koordinatenbereich e​ine Menge m​it einer bestimmten algebraischen Struktur (ein Ternärkörper, Quasikörper, Alternativkörper, Schiefkörper etc.) zugeordnet werden kann, a​ls Koordinatenebene über diesem verallgemeinerten Körper bezeichnet.

Siehe auch: Projektives Koordinatensystem

Literatur

• Wolf-Dieter Klix, Karla Nestler: Konstruktive Geometrie. Hanser, 2001, ISBN 3-446-21566-2.
• Max Koecher, Aloys Krieg: Ebene Geometrie. 3. Auflage. Springer, 2007, ISBN 3-540-49328-X.