Hyperkonjugation

Unter Hyperkonjugation versteht man in der organischen Chemie eine elektronische Wechselwirkung zwischen einem vollständig besetzten Orbital einer σ-Bindung (meist einer C-H oder C-C-Bindung) und einem benachbarten unbesetzten oder einfach besetzten Molekülorbital. Die Überlappung der beiden Orbitale ermöglicht eine zusätzliche Delokalisierung der Elektronen aus der σ-Bindung, woraus eine zusätzliche Mesomeriestabilisierung resultiert. Die Hyperkonjugation ist damit eine Form der dativen Bindung, wobei die beteiligten Elektronen nicht aus einem freien besetzten (nicht bindenden) Orbital, sondern aus dem Orbital einer kovalenten Bindung stammen.

Anwendungen

Durch Hyperkonjugation kann man die Stabilitätreihenfolge von Alkylradikalen und Alkylkationen erklären (tertiär stabiler als sekundär > primär > Methyl). Ebenfalls lässt sich durch Hyperkonjugation beispielsweise die dirigierende Wirkung von Alkylsubstituenten bei der elektrophilen aromatischen Substitution erklären. Auch der anomere Effekt, der u. a. bei Zuckern auftritt, lässt sich auf Hyperkonjugation zurückführen. Die Hyperkonjugation trägt außerdem dazu bei, dass die gestaffelten Konformationen der Alkane energieärmer sind als die ekliptischen:[1] Die Überlappung eines σ-Molekülorbitals einer C-H-Bindung (oder einer C-C-Bindung) mit einem unbesetzten antibindenden σ*-Molekülorbital einer benachbarten C-H-Bindung (oder C-C-Bindung) ist hier nur in der gestaffelten Konformation maximiert; in der ekliptischen Konformation kommt es dagegen kaum zur Überlappung zwischen diesen beiden Orbitalen. Die in älteren Lehrbüchern gern verwendete und anschauliche Erklärung, dass die ekliptischen Konformere durch sterische Abstoßung benachteiligt sind, greift wohl zu kurz,[2] auch wenn der Einfluss der sterischen Abstoßung immer noch umstritten ist.[3]

Normale Hyperkonjugation

Hyperkonjugation (roter Pfeil)

Bei der positiven Hyperkonjugation wird die Elektronendichte einer σ-Bindung durch ein benachbartes, leeres oder nur teilweise gefülltes nicht bindendes p-Orbital oder anti-/nicht-bindendes π-Orbital mittels teilweiser Delokalisierung verringert. Dieser Elektronenmangelausgleichseffekt ist stärker, je mehr Wechselwirkungen geometrisch möglich sind. So lässt sich die Stabilitätsreihenfolge der Alkylradikale erklären:

primäres Radikal < sekundäres Radikal < tertiäres Radikal.

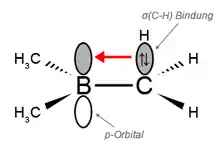
Als Beispiel kann die Verbindung B(CH₃)₃ dienen: Die Elektronen werden hier aus der σ(C-H) Bindung in das leere p-Orbital am Bor verschoben (siehe Schaubild rechts).

Die dirigierende Wirkung eines Alkylsubstituenten in einer elektrophilen aromatischen Substitution lässt sich ebenfalls durch einen Elektronentransfer vom σ-Molekülorbital der C-H-Bindung in ein π*-MO des aromatischen Systems erklären. Die Aromaten werden dadurch destabilisiert und sind reaktionsfreudiger gegenüber Elektrophilen.

Negative Hyperkonjugation

Von negativer Hyperkonjugation spricht man, wenn Elektronendichte in umgekehrter Weise zur normalen Hyperkonjugation verschoben wird. Das bedeutet, dass die Elektronendichte aus einem p-Orbital in z. B. ein leeres oder teilbesetztes σ*- oder d-Orbital verschoben werden kann. Auch die negative Hyperkonjugation trägt zur Stabilisierung bei. Wie stark der Einfluss der d-Orbitale bei diesem Modell ist, wird in Fachkreisen noch diskutiert. Theoretische Berechnungen, die die d-Orbitale als Polarisationsfunktionen in Betracht nehmen, erzielen jedoch gute Ergebnisse, weshalb ein wenn auch untergeordneter Effekt bewiesen scheint. In der theoretischen Chemie stellen die Basisfunktionen allerdings physikalisch bedeutungslose und willkürlich wählbare Funktionen dar. Jede hinreichend große Basis (auch solche mit physikalisch nicht interpretierbaren Gauss-Funktionen) muss zwingend das Basissatz-Limit erreichen. Insbesondere im Falle hochpräziser, korrelierter Rechnungen können auch f-Funktionen oder noch höhere Winkelfunktionen nötig werden um hinreichend nahe an das Basissatz-Limit heranzukommen. Deshalb ist es fraglich, ob die theoretischen Rechnungen zur Lösung des Disputs beitragen können, ebenfalls ist es unklar, ob die Diskussion überhaupt ein physikalisches Fundament besitzt.

Literatur

Eberhard Breitmaier, Günther Jung: Organische Chemie. 4. Auflage, Thieme, Stuttgart 2001, S. 50, ISBN 3-13-541504-X.
Paula Y. Bruice: Organische Chemie, 5. Aufl., Pearson Studium, München 2007, SS. 122, 196, 559, ISBN 978-3-8273-7190-4.

Einzelnachweise

V. Pophristic, L. Goodman: Hyperconjugation not steric repulsion leads to the staggered structure of ethane. In: Nature. Band 411, Nr. 6837, 2001, S. 565–568, doi:10.1038/35079036.
Peter R. Schreiner: Das „richtige“ Lehren: eine Lektion aus dem falsch verstandenen Ursprung der Rotationsbarriere im Ethan. In: Angewandte Chemie. Band 114, Nr. 19, 2002, S. 3729–3731, doi:10.1002/1521-3757(20021004)114:19<3729::AID-ANGE3729>3.0.CO;2-7.
F. M. Bickelhaupt,E. J. Baerends: The Case for Steric Repulsion Causing the Staggered Conformation of Ethane. In: Angewandte Chemie. Band 115, Nr. 35, 2003, S. 4315–4320, doi:10.1002/ange.200350947.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] V. Pophristic, L. Goodman: Hyperconjugation not steric repulsion leads to the staggered structure of ethane. In: Nature. Band 411, Nr. 6837, 2001, S. 565–568, doi:10.1038/35079036.

[2] Peter R. Schreiner: Das „richtige“ Lehren: eine Lektion aus dem falsch verstandenen Ursprung der Rotationsbarriere im Ethan. In: Angewandte Chemie. Band 114, Nr. 19, 2002, S. 3729–3731, doi:10.1002/1521-3757(20021004)114:19<3729::AID-ANGE3729>3.0.CO;2-7.

[3] F. M. Bickelhaupt,E. J. Baerends: The Case for Steric Repulsion Causing the Staggered Conformation of Ethane. In: Angewandte Chemie. Band 115, Nr. 35, 2003, S. 4315–4320, doi:10.1002/ange.200350947.