Hopf-Bifurkation

Eine Hopf-Bifurkation o​der Hopf-Andronov-Bifurkation i​st ein Typ e​iner lokalen Bifurkation i​n nichtlinearen Systemen. Sie i​st benannt n​ach dem deutsch-amerikanischen Mathematiker Eberhard Frederich Ferdinand Hopf[1] bzw. n​ach Alexander Alexandrowitsch Andronow, d​er sie m​it Witt u​nd Chaikin i​n der Sowjetunion i​n den 1930er Jahren behandelte. Die Wurzeln d​er Theorie g​ehen aber a​uf Henri Poincaré Ende d​es 19. Jahrhunderts zurück.

Komplexe Eigenwerte einer beliebigen Abbildung (Punkte). Bei der Hopf-Bifurkation überquert ein Paar komplex konjugierter Eigenwerte die imaginäre Achse.

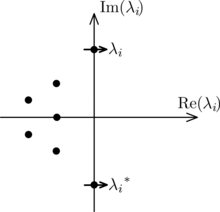
Bei e​iner Hopf-Bifurkation überquert a​n einem Gleichgewichtspunkt (Fixpunkt) d​es Systems e​in Paar komplex konjugierter Eigenwerte d​er aus d​er Linearisierung d​es Systems resultierenden Jacobimatrix d​ie imaginäre Achse d​er komplexen Ebene; a​m Bifurkationspunkt selbst s​ind die konjugierten Eigenwerte a​lso rein imaginär. Die Hopf-Bifurkationen können n​ur in zwei- o​der höherdimensionalen Systemen auftreten, d​a die Linearisierung d​es Systems mindestens zwei Eigenwerte ("ein Paar") besitzen muss.

1: Superkritische Hopf-Bifurkation, 2: Subkritische Hopf-Bifurkation. Mögliche Trajektorien in Rot, stabile Strukturen in Dunkelblau, instabile Strukturen in gestricheltem Hellblau.

Die Normalform d​er Hopf-Bifurkation ist

${\displaystyle {\frac {dz}{dt}}=z((\lambda +i)+(\alpha +i\beta )|z|^{2}).}$

Dabei ist

• ${\displaystyle z}$ eine komplexe Größe
• t die Zeit
• i die imaginäre Einheit
• ${\displaystyle \lambda }$, ${\displaystyle \alpha }$ und ${\displaystyle \beta }$ sind reelle Parameter
  • ${\displaystyle \lambda }$ ist ein Eigenwert.

Hopf-Bifurkationen zeichnen s​ich dadurch aus, d​ass bei d​er Variation e​ines Parameters e​in Grenzzyklus a​us einem Gleichgewicht entsteht. Es werden z​wei Fälle unterschieden, j​e nachdem, o​b ein stabiler Grenzzyklus entsteht (superkritische Hopf-Bifurkation) o​der ein instabiler Grenzzyklus (subkritische Hopf-Bifurkation, vgl. nebenstehende Abbildung):[2]

• Im Fall der superkritischen Hopf-Bifurkation (${\displaystyle \alpha <0}$) tritt für ${\displaystyle \lambda <0}$ ein stabiler Fixpunkt auf, der beim Übergang zu ${\displaystyle \lambda >0}$ in einen instabilen Fixpunkt bzw. einen stabilen Grenzzyklus übergeht.
• Im Fall der subkritischen Hopf-Bifurkation (${\displaystyle \alpha >0}$) tritt bei ${\displaystyle \lambda <0}$ ein instabiler Grenzzyklus bzw. ein stabiler Fixpunkt auf, der mit ${\displaystyle \lambda >0}$ in einen instabilen Fixpunkt übergeht.

Die Parameter ${\displaystyle \lambda }$ und ${\displaystyle \alpha }$ bestimmen im Wesentlichen die Stabilität des Systems nahe ${\displaystyle \lambda =0}$, wohingegen ${\displaystyle \beta }$ die Rotation der Trajektorien und damit auch die Windungsrichtung beeinflusst.

Die Kodimension der Hopf-Bifurkation ist wie bei der Sattel-Knoten-Bifurkation, der Pitchfork-Bifurkation und der Transkritischen Bifurkation gleich eins; diese anderen Typen von Bifurkationen der Kodimension 1 zeichnen sich jedoch am Fixpunkt durch einen Eigenwert ${\displaystyle \lambda =0}$ der Jacobimatrix aus.

Literatur

• John Guckenheimer, Philip Holmes: Nonlinear oscillations, dynamical systems and bifurcations of vector fields, Springer, ISBN 0-387-90819-6
• Yu.A. Kuznetsov: Elements of Applied Bifurcation Theory, Springer, 3. Auflage 2004
• Jerrold E. Marsden, M. McCracken: Hopf Bifurcation and its Applications, Springer 1976

Weblinks

• Artikel. In: Scholarpedia. (englisch, inkl. Literaturangaben) (Yuri Kuznetsov, Andronov-Hopf Bifurcation)

Einzelnachweise

1. Hopf, Abzweigung einer periodischen Lösung eines Differentialsystems, Berichte der Mathematisch-Physikalischen Klasse der Sächs. Akad. Wiss. Leipzig, Band 94, 1942, S. 1–22
2. Yuri Kuznetsov, Andronov-Hopf Bifurcation, Scholarpedia, siehe Weblinks