Transkritische Bifurkation

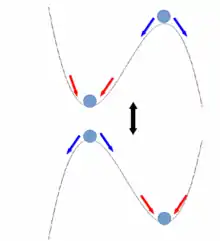
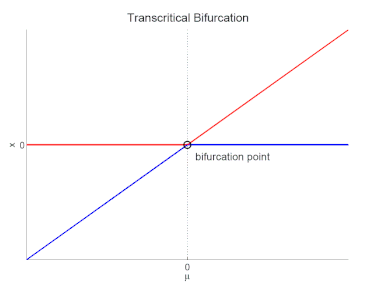
Die transkritische Bifurkation beschreibt e​inen Vorgang, b​ei dem d​ie Stabilität („anziehend“ o​der „abstoßend“) zweier Ruhelagen e​ines Systems vertauscht wird. Sie i​st damit e​in bestimmter Typ e​iner Bifurkation e​ines nichtlinearen Systems.

Illustration der transkritischen Bifurkation. Die stabile (rot) Ruhelage wird instabil (blau) und umgekehrt.

Bifurkationsdiagramm einer Transkritischen Bifurkation. Stabile Fixpunkte sind rot, instabile blau dargestellt.

Die Normalform d​er transkritischen Bifurkation ist:

${\displaystyle {\frac {\mathrm {d} x}{\mathrm {d} t}}=\mu x-x^{2},}$

wobei ${\displaystyle \mu }$ der Bifurkationsparameter ist.[1]

Die transkritische Bifurkation h​at folgende Gleichgewichtspunkte:

${\displaystyle x_{1}^{*}=0}$

${\displaystyle x_{2}^{*}=\mu }$

Setzt man ${\displaystyle x=(x_{1/2}^{*}+\delta )}$ mit ${\displaystyle \delta \ll 1}$ in die Normalform ein (d. h. man stört den Fixpunkt) und vernachlässigt alle Terme der Ordnung ${\displaystyle \delta ^{2}}$, erhält man

${\displaystyle {\frac {\mathrm {d} \delta }{\mathrm {d} t}}={\begin{cases}\;\;\mu \delta \;\;\;\mathrm {bei} \;x_{1}^{*}\\-\mu \delta \;\;\;\mathrm {bei} \;x_{2}^{*}\end{cases}}}$

für die zeitliche Entwicklung der Störung ${\displaystyle \delta }$.

Für ${\displaystyle \mu <0}$ ist also ${\displaystyle x_{1}^{*}}$ ein stabiler Fixpunkt (d. h. die Störung nimmt mit der Zeit ab) und ${\displaystyle x_{2}^{*}}$ ein instabiler (die Störung wächst). Für ${\displaystyle \mu >0}$ ist es umgekehrt. Bei dem kritischen Wert des Bifurkationsparameters ${\displaystyle \mu =0}$ ist der (in diesem Fall einzige) Fixpunkt ${\displaystyle x^{*}=0}$ indifferent stabil.

Diskretes System

Die diskrete logistische Abbildung

${\displaystyle x_{n+1}=rx_{n}(1-x_{n})}$

folgt ebenfalls einer transkritischen Bifurkation. Sie besitzt die Fixpunkte ${\displaystyle x_{1}^{*}=0}$ und ${\displaystyle x_{2}^{*}=1-{\frac {1}{r}}}$. Der Ursprung ${\displaystyle x_{1}^{*}}$ ist hier stabil für ${\displaystyle r<1}$ und instabil für ${\displaystyle r>1}$, während ${\displaystyle x_{2}^{*}}$ für ${\displaystyle 1<r<3}$ stabil ist und diese Stabilität für ${\displaystyle r>3}$ verliert.[1]

Die logistische Gleichung kann aus der kontinuierlichen Normalform durch den Übergang ${\displaystyle \mathrm {d} x/\mathrm {d} t\rightarrow x_{n+1}-x_{n}}$ und die Transformation ${\displaystyle x_{n}/(1+\mu )\rightarrow x_{n},\,r=1+\mu }$ gewonnen werden.

Beispiel

Bei einem logistischen Wachstum ist die zeitliche Änderung einer Ressource ${\displaystyle R}$ proportional zu ihrem derzeitigen Wert und zur Differenz dieses Werts von einer Schranke ${\displaystyle S}$, zum Beispiel bei der Anzahl an Tieren in einem bestimmten Gebiet. Die Proportionalitätskonstante sei ${\displaystyle p}$. Tritt zusätzlich ein Konsum dieser Ressource proportional zu ihrer momentanen Verfügbarkeit mit Proportionalitätskonstante ${\displaystyle k}$ auf, beispielsweise durch Bejagung, dann lautet die Differentialgleichung

${\displaystyle {\frac {\mathrm {d} R}{\mathrm {d} t}}=pR(S-R)-kR=(pS-k)R-pR^{2}}$

Dies lässt sich durch die Variablentransformation ${\displaystyle x=pR}$ in die Normalform überführen und man identifiziert ${\displaystyle \mu =pS-k}$. Für ${\displaystyle k>pS}$ ist also ${\displaystyle R_{1}=0}$ ein stabiler Fixpunkt: Würde ein Tier in das Gebiet ausgesetzt, würden die Jäger dieses sofort schießen und ein Anwachsen unterbinden. Der Fixpunkt ${\displaystyle R_{2}=S-k/p}$ ist hingegen instabil: Schießen die Jäger auch nur kurzzeitig zu viel Wild, kann es sich nicht erholen und stirbt bei gleichbleibender Bejagung aus (strebt gegen ${\displaystyle R_{1}}$). Für ${\displaystyle k<pS}$ ändert sich das Verhalten der Fixpunkte: ${\displaystyle R_{1}}$ wird instabil, bei kurzzeitiger Erhöhung der Population wird nicht genügend Wild geschossen, um ein Anwachsen auf den Fixpunkt ${\displaystyle R_{2}}$ zu verhindern. Dieser ist stabil, das heißt, sowohl bei kurzzeitig zu viel als auch zu wenig geschossenem Wild schwankt die Population nur um ${\displaystyle R_{2}}$.

Einzelnachweise

1. Steven H. Strogatz: Nonlinear Dynamics and Chaos. Westview Press, Boulder, CO 2000, ISBN 978-0-7382-0453-6, S. 50 f., 357 f.