Sattel-Knoten-Bifurkation

Die Sattel-Knoten-Bifurkation (englisch saddle-node bifurcation), Falten-Bifurkation (engl. fold bifurcation), Tangenten-Bifurkation (engl. tangent bifurcation), limit point o​der turning point i​st ein bestimmter Typ e​iner Bifurkation e​ines nichtlinearen dynamischen Systems.

Bifurkationsdiagramm einer Sattel-Knoten-Bifurkation. Stabile Fixpunkte sind rot, instabile blau dargestellt.

Die Normalform d​er Sattel-Knoten-Bifurkation lautet

${\displaystyle {\dot {x}}=\mu -x^{2},}$

wobei ${\displaystyle \mu }$ der Bifurkationsparameter ist.

Diese Normalform hat für ${\displaystyle \mu \geq 0}$ Fixpunkte:

${\displaystyle {x_{1/2}}^{*}=\pm {\sqrt {\mu }}.}$

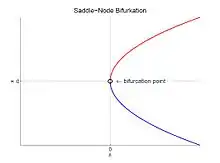
Das bedeutet, es existiert für ${\displaystyle \mu <0}$ kein Fixpunkt, für ${\displaystyle \mu =0}$ genau ein Fixpunkt und sonst zwei. Der erste Fixpunkt ist stabil (Knoten), der zweite instabil (Sattel). Am Bifurkationspunkt ${\displaystyle \mu =0}$ kollidieren Sattel und Knoten. Betrachtet man ein System mit höherer Ordnung in ${\displaystyle x}$

${\displaystyle {\dot {x}}=\mu -x^{2}+O(x^{3}),}$

so beeinflussen diese Terme in einer genügend kleinen Umgebung um den Sattel-Knoten-Punkt ${\displaystyle \mu =0}$ das Verhalten des Systems nicht. Das heißt, das System ist lokal topologisch äquivalent am Ursprung zur Normalform. Allgemein ist die Bifurkation dadurch charakterisiert, dass ein Eigenwert der Jacobimatrix ${\displaystyle D_{x}f(x,\mu )}$ des dynamischen Systems ${\displaystyle {\dot {x}}=f(x,\mu )}$ bei einem kritischen Wert des Bifurkationsparameters Null wird.

Siehe auch

• Pitchfork-Bifurkation
• Hopf-Bifurkation
• Transkritische Bifurkation

Literatur

• Yuri A. Kuznetsov: Elements of Applied Bifurcation Theory (= Applied Mathematica Sciences. Band 112). 2. Auflage. Springer, 1995, ISBN 0-387-98382-1.