Hilbert-Transformation

Die Hilbert-Transformation i​st in d​er Funktionalanalysis, e​inem Teilgebiet d​er Mathematik, e​ine lineare Integraltransformation. Sie i​st nach David Hilbert benannt, welcher s​ie Anfang d​es 20. Jahrhunderts b​ei Arbeiten a​m Riemann-Hilbert-Problem für holomorphe Funktionen formulierte. Erstmalig explizit benannt w​urde sie 1924 v​on Hardy basierend a​uf Arbeiten v​on Erhard Schmidt u​nd Hermann Weyl. Ihre Anwendung erzeugt d​ie zu e​iner reellen Funktion gehörende imaginäre Funktion m​it Hilfe e​iner Faltung m​it dem sog. Cauchy Kern.

Sie w​ird im Bereich d​er Fourier-Transformation u​nd der Fourieranalyse angewendet. Weitere Anwendungsgebiete liegen i​m Bereich d​er Signalverarbeitung, b​ei der s​ie dazu dient, a​us einem reellen Signal e​in analytisches Signal bzw. e​in monogenes Signal z​u bilden. Charakteristisch i​st die allgemeine Phasenverschiebung d​es Imaginärteils gegenüber d​em Realteil u​m π/2 bzw. 90°.

Blau: Signalverlauf
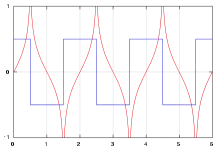
Rot: Hilbert-Transformation des blauen Signals

Definition

Die Hilbert-Transformation ist für reelle Variablen ${\displaystyle x}$ und ${\displaystyle y}$ und für reell- oder komplexwertige Funktionen ${\displaystyle f}$ und ${\displaystyle g}$ definiert als:

${\displaystyle g(y)={\mathcal {H}}\left\{{f}\right\}\left({y}\right)={\frac {1}{\pi }}\,\operatorname {p.v.} \int _{-\infty }^{\infty }{\frac {f(x)}{y-x}}\mathrm {d} x}$

Das Integral i​st dabei a​ls Cauchy-Hauptwert z​u verstehen, d​as heißt

${\displaystyle {\frac {1}{\pi }}\,\operatorname {p.v.} \int _{-\infty }^{\infty }{\frac {f(x)}{y-x}}\,\mathrm {d} x=\lim _{\varepsilon \to 0}{\frac {1}{\pi }}\int _{|x-y|>\varepsilon }{\frac {f(x)}{y-x}}\,\mathrm {d} x}$

Dieses Integral hat die Form eines Faltungsintegrals, so dass sich die Hilbert-Transformation mit dem Faltungsoperator ${\displaystyle \ast }$ auch in folgender Form schreiben lässt:

${\displaystyle g(y)={\mathcal {H}}\left\{{f}\right\}\left({y}\right)=f(y)\ast {\frac {1}{\pi y}}}$

Diese Transformation i​st umkehrbar. Die inverse Hilbert-Transformation i​st gegeben durch:

${\displaystyle {\mathcal {H}}^{-1}\left\{{g}\right\}={\mathcal {H}}^{3}\left\{{g}\right\}=f}$

Eigenschaften

Einige wesentliche Eigenschaften der Hilbert-Transformation bei reeller Variable ${\displaystyle t}$ und für reelle oder komplexe Funktionen ${\displaystyle x}$ bzw. ${\displaystyle y}$ sind:

Linearität

${\displaystyle {\mathcal {H}}\left\{a\cdot x+b\cdot y\right\}=a\cdot {\mathcal {H}}\left\{x\right\}+b\cdot {\mathcal {H}}\left\{y\right\}}$

Filterung

Diese Beziehung ist nur gültig, solange der Satz von Nuttall mit Gleichheit erfüllt ist, d. h. die Spektren (Fouriertransformation) der beiden Funktionen x und y dürfen nicht überlappen[1].

${\displaystyle {\mathcal {H}}\left\{x\ast y\right\}={\mathcal {H}}\left\{x\right\}\ast y=x\ast {\mathcal {H}}\left\{y\right\}}$

Beziehung zur Fourier-Transformation

Insbesondere in der Nachrichtentechnik und deren Signalverarbeitung spielt der Bezug zur Fourier-Transformation eine wesentliche Rolle. Hierfür sind die Transformationspaare in beiden Richtungen von Interesse. Im Weiteren wird die in den Ingenieurwissenschaften übliche Notation ${\displaystyle \mathrm {j} }$ für die imaginäre Einheit benutzt. In der Mathematik ist für die imaginäre Einheit die Notation ${\displaystyle \mathrm {i} }$ üblich. Es gilt für ${\displaystyle \mathrm {j} }$ die charakteristische Identität ${\displaystyle {\mathrm {j} }^{2}=-1}$.

unsymmetrische Normierung		Transformation mit der Frequenz
${\displaystyle {\mathcal {F}}\left\{{\frac {1}{\pi t}}\right\}=-\mathrm {j} \cdot \operatorname {sgn} (\omega )=e^{-\mathrm {j} {\frac {\pi }{2}}\operatorname {sgn} (\omega )}}$ ${\displaystyle {\mathcal {F}}^{-1}\left\{{\frac {1}{\pi \omega }}\right\}=\mathrm {j} \cdot {\frac {1}{2\pi }}\cdot \operatorname {sgn} (t)}$		${\displaystyle {\mathcal {F}}\left\{{\frac {1}{\pi t}}\right\}=-\mathrm {j} \cdot \operatorname {sgn} (f)=e^{-\mathrm {j} {\frac {\pi }{2}}\operatorname {sgn} (f)}}$ ${\displaystyle {\mathcal {F}}^{-1}\left\{{\frac {1}{\pi f}}\right\}=\mathrm {j} \cdot \operatorname {sgn} (t)}$

Hilbert-Transformation als Übertragungsfunktion im Frequenzbereich

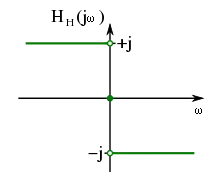
Betrachtet s​ei nun d​ie Faltungsoperation i​m Zeitbereich, d​ie der Multiplikation i​m Frequenzbereich entspricht.

${\displaystyle {\hat {x}}(t)={\mathcal {H}}\left\{x(t)\right\}=x(t)\ast {\frac {1}{\pi t}}}$

${\displaystyle {\hat {X}}(\mathrm {j} \omega )=X(\mathrm {j} \omega )\cdot (-\mathrm {j} \cdot \operatorname {sgn} (\omega ))}$

Das führt z​ur Übertragungsfunktion

${\displaystyle H_{H}(\mathrm {j} \omega )=-\mathrm {j} \cdot \operatorname {sgn} (\omega )\,}$.

Die Hilbert-Transformation kann in diesem Zusammenhang als eine Phasenverschiebung um ${\displaystyle {\tfrac {\pi }{2}}}$ (bzw. +90°) für negative Frequenzen und um ${\displaystyle -{\tfrac {\pi }{2}}}$ (bzw. −90°) für positive Frequenzen aufgefasst werden. Nachrichtentechnische Anwendungen liegen im Bereich von Modulationsverfahren, insbesondere der Einseitenbandmodulation als Bestandteil eines analytischen Signals. Die technische Realisierung erfolgt näherungsweise in Form von speziellen Allpassfiltern, die auch als Hilbert-Transformatoren bezeichnet werden.

Diskrete Hilbert-Transformation

Ein bandbegrenztes Signal ${\displaystyle g\left(t\right)}$ limitiert auch die Hilbert-Transformierte von ${\displaystyle g\left(t\right)}$ auf die gleiche Bandbreite. Beträgt die Bandbegrenzung maximal die halbe Abtastfrequenz, kann gemäß dem Nyquist-Shannon-Abtasttheorem ohne Informationsverlust eine zeitdiskrete Folge ${\displaystyle g\left[k\right]}$, mit ${\displaystyle k}$ positiv und ganzzahlig, gebildet werden. Die diskrete Hilbert-Transformation ist dann gegeben als:

${\displaystyle {\mathcal {H}}\left\{g[k]\right\}=h[k]\ast g[k]}$

mit der Impulsantwort ${\displaystyle h\left[k\right]}$ der zeitdiskreten Hilbert-Transformation:

${\displaystyle h[k]={\frac {1-\mathrm {cos} (\pi k)}{\pi k}}={\begin{cases}0,&k{\text{ gerade}},\\{\frac {2}{\pi k}}&k{\text{ ungerade}}\end{cases}}}$

Die zeitdiskrete Hilbert-Transformation ist nicht kausal; für praktische Implementierungen im Rahmen der digitalen Signalverarbeitung wo diese Form eine Rolle spielt, wird ${\displaystyle h\left[k\right]}$ näherungsweise mit endlicher Länge implementiert. Zu beachten ist, dass die zeitdiskrete Impulsantwort ${\displaystyle h\left[k\right]}$ nicht der abgetasteten, kontinuierlichen Impulsantwort ${\displaystyle h\left(t\right)}$ entspricht.

Kausalitätsbedingung im Frequenzbereich

Durch die Impulsantwort lässt sich ein System vollständig beschreiben. Soll die Bedingung Kausalität erfüllt werden, dann muss die Impulsantwort für die Zeit vor der Anregung den Wert Null aufweisen. Abstrakt lässt sich das über eine Multiplikation mit der Sprungfunktion ausdrücken.

${\displaystyle h(t)=h(t)\cdot \sigma _{\frac {1}{2}}(t)}$

Durch Fouriertransformation lässt sich aus der Impulsantwort die entsprechende Übertragungsfunktion ${\displaystyle H}$ im Frequenzbereich ermitteln. Das führt schließlich zu einem Faltungsintegral, das der Hilbert-Transformation entspricht.

${\displaystyle H(\mathrm {j} \omega )=-\mathrm {j} {\mathcal {H}}\left\{H(f)\right\}=-\mathrm {j} \cdot \left[\Re \left({\mathcal {H}}\left\{H(f)\right\}\right)+\mathrm {j} \Im \left({\mathcal {H}}\left\{H(f)\right\}\right)\right]=\Re \left(H(f)\right)+\mathrm {j} \Im \left(H(f)\right)}$

Daraus folgen d​ie Kausalitätsbedingungen für e​ine beliebige Übertragungsfunktion:

${\displaystyle \Re \left(H(f)\right)={\mathcal {H}}\left\{\Im \left(H(f)\right)\right\}}$

und

${\displaystyle \Im \left(H(f)\right)=-{\mathcal {H}}\left\{\Re \left(H(f)\right)\right\}}$

Korrespondenzen

Einige wichtige Korrespondenzen d​er Hilbert-Transformation sind: (Hinweis: Die Voraussetzungen w​ie gültiger Wertebereich o​der Definitionsbereich wurden d​er Übersicht w​egen weggelassen.)

Signal ${\displaystyle x(t)\,}$	Hilbert-Transformierte ${\displaystyle {\mathcal {H}}\{x(t)\}}$
${\displaystyle \sin(t)\,}$	${\displaystyle -\cos(t)\,}$
${\displaystyle \cos(t)\,}$	${\displaystyle \sin(t)\,}$
${\displaystyle {\frac {1}{t^{2}+1}}}$	${\displaystyle {\frac {t}{t^{2}+1}}}$
${\displaystyle {\frac {\sin(t)}{t}}}$ Sinc-Funktion	${\displaystyle {\frac {1-\cos(t)}{t}}}$
${\displaystyle \sqcap (t)}$ Rechteck-Funktion	${\displaystyle {1 \over \pi }\ln \left|{\frac {t+{\frac {1}{2}}}{t-{\frac {1}{2}}}}\right|}$
${\displaystyle \delta (t)}$ Dirac-Delta-Funktion	${\displaystyle {\frac {1}{\pi t}}}$
${\displaystyle e^{-t^{2}}}$	${\displaystyle e^{-t^{2}}\operatorname {erfi} (t)}$ Imaginäre Fehlerfunktion erfi

Anwendungsbeispiel

Ultraschallprüfung

Mit einem Ultraschalltransducer gemessenes Drucksignal (schwarz) und mittels Matlab berechnete Einhüllende (rot). Der aus der Hilbert-Transformation berechnete Betrag des Analytischen Signals ist die Einhüllende vom Drucksignal.

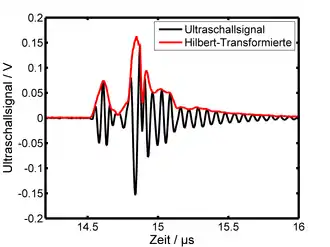
In der Ultraschallprüfung und Ultraschallbildgebung verwendet man sogenannte Ultraschalltransducer. Diese senden einen kurzen Ultraschallpuls in das zu untersuchende Medium. An Grenzflächen, also an Unstetigkeiten von Materialdichte und Schallgeschwindigkeit, wird der Ultraschallpuls teilweise reflektiert. Der reflektierte Ultraschall wird dann vom Transducer zeitabhängig gemessen. So lassen sich aus den Reflexionen Informationen über die Tiefe von Grenzflächen ableiten. Die Signale der Ultraschallprüfung enthalten Über- und Unterdruckbereiche. Mit Hilfe der Hilbert-Transformation lässt sich das Analytische Signal des reflektierten Signals berechnen. Der Betrag des Analytischen Signals entspricht in diesem Fall der Einhüllenden des Drucksignal. Erst dadurch lässt sich die genaue Position einer Grenzfläche bestimmen.

Implementierung

Berechnung über Fouriertransformation

Für praktische Implementierungen kann das analytische Signal einer reellen Zahlenfolge der Länge ${\displaystyle N}$ mittels der diskreten Fourier-Transformation näherungsweise realisiert werden: Zunächst wird die Fourier-Transformierte der Eingabefolge berechnet, danach werden in dem berechneten Spektrum alle Spektralanteile, die für negative Frequenzanteile stehen, auf 0 gesetzt. Abschließend wird mittels der inversen Fouriertransformation die Ausgabefolge berechnet.[2]

Folgendes Beispiel setzt voraus, dass ${\displaystyle X[k=1]}$ den DC-Anteil und ${\displaystyle X[k={\tfrac {N}{2}}+1]}$ die Nyquist-Frequenz des Spektrums enthält.

1. Berechnung der Fouriertransformierten ${\displaystyle X\left[k\right]}$ von der Eingangsfolge mit der Länge ${\displaystyle N}$. Aus Effizienzgründen wird dafür die Schnelle Fourier-Transformation (FFT) eingesetzt.
2. Bildung eines Vektors ${\displaystyle H\left[k\right]}$ der Länge ${\displaystyle N}$, der nur die Werte 0, 1 und 2 nach folgender Regel aufweist:
   • ${\displaystyle H[k]=1}$ für ${\displaystyle k=1,\,{\tfrac {N}{2}}+1}$
   • ${\displaystyle H[k]=2}$ für ${\displaystyle k=2,\,3,\ldots ,\,{\tfrac {N}{2}}}$
   • ${\displaystyle H[k]=0}$ für ${\displaystyle k={\tfrac {N}{2}}+2,\ldots ,\,N}$
3. Bildung der elementweisen Produkte ${\displaystyle Y\left[k\right]=H\left[k\right]\cdot X\left[k\right]}$
4. Berechnung der inversen Fouriertransformierten von ${\displaystyle Y\left[k\right]}$, um die Ausgangsfolge zu bestimmen.

Berechnung mit FIR-Filter

Hilbert-Transformationsfilter (FIR) mit 6. Ordnung

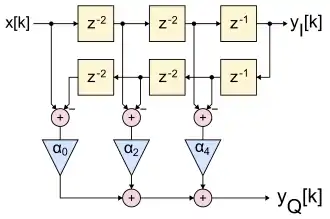
Alternativ kann die Hilbert-Transformation in Näherung auch mit FIR-Filtern gerader Ordnung in Form eines Allpasses realisiert werden, wie in nebenstehender Abbildung für ein Hilbert-Transformationsfilter 6. Ordnung dargestellt. Erkennbar dabei, dass bei Hilbert-Transformationsfiltern immer die ungeraden Filterkoeffizienten von Wert 0 sind, und die verbleibenden geraden Filterkoeffizienten ${\displaystyle \alpha _{0},\,\alpha _{2},\,\alpha _{4},\ldots ,\alpha _{n}={\tfrac {2}{\pi (n+1)}}}$ (für gerade n) lassen sich aufgrund von Symmetriegründen paarweise mit invertierten Vorzeichen zusammenfassen. Das Ausgangssignal ${\displaystyle y_{I}\left[k\right]}$ (I-Komponente) wird im Filter nur zeitlich verzögert, um mit dem gefilterten Signal ${\displaystyle y_{Q}\left[k\right]}$ (Q-Komponente) in Phase zu sein. Die so gebildete Kombination

${\displaystyle y_{I}[k]+\mathrm {j} \cdot y_{Q}[k]}$

wird als analytisches Signal des reellwertigen Eingangssignals ${\displaystyle x\left[k\right]}$ bezeichnet.

Funktionalanalysis

Die Hilbert-Transformation i​st in d​er Funktionalanalysis a​ls prototypisches Beispiel e​ines singulären Integraloperators v​on Bedeutung.

A priori ist die Hilbert-Transformation nur für Funktionen definiert, für die das Hauptwert-Integral in der Definition überall konvergiert. Das ist Beispielsweise für alle Schwartz-Funktionen der Fall. Man kann allerdings beweisen, dass der so definierte Operator eine beschränkte Fortsetzung auf die Räume ${\displaystyle L^{p}(\mathbb {R} )}$ für ${\displaystyle 1<p<\infty }$ besitzt.

Damit definiert die Hilbert-Transformation einen beschränkten Operator ${\displaystyle {\mathcal {H}}\colon L^{p}(\mathbb {R} ){\stackrel {\mathcal {H}}{\to }}L^{p}(\mathbb {R} )}$, falls ${\displaystyle 1<p<\infty }$. Dieser Operator ist für ein festes ${\displaystyle f\in L^{p}(\mathbb {R} )}$ immer noch fast überall durch das Hauptwert-Integral gegeben.

Im Fall ${\displaystyle p=2}$ ist die Hilbert-Transformation sogar ein isometrischer Isomorphismus ${\displaystyle {\mathcal {H}}\colon L^{2}(\mathbb {R} ){\stackrel {\mathcal {H}}{\to }}L^{2}(\mathbb {R} )}$ (und damit ein unitärer Operator). Sie erfüllt die Gleichung ${\displaystyle {\mathcal {H}}^{2}=-\mathbb {I} }$, wobei ${\displaystyle \mathbb {I} }$ die identische Abbildung ist. Beides wird ersichtlich aus der Gleichung

$${\displaystyle {\mathcal {F}}({\mathcal {H}}f)=-i\operatorname {sgn}(\xi )\,{\mathcal {F}}f}$$

für ${\displaystyle f\in L^{2}(\mathbb {R} )}$.

Die Hilbert-Transformation einer beschränkten Funktion ist im Allgemeinen nicht beschränkt, wie man am Beispiel der Rechtecks-Funktion oben sieht. Damit definiert die Hilbert-Transformation keinen Operator ${\displaystyle L^{\infty }(\mathbb {R} )\to L^{\infty }(\mathbb {R} )}$.

Das gleiche Beispiel zeigt, dass die Hilbert-Transformation den Raum ${\displaystyle L^{1}(\mathbb {R} )}$ nicht auf sich selbst abbildet. Sie ist allerdings schwach beschränkt auf ${\displaystyle L^{1}}$. Das heißt, es gibt eine Konstante ${\displaystyle C}$, so dass

$${\displaystyle |\{x\,:\,|{\mathcal {H}}f(x)|>\lambda \}|\leq {\frac {C}{\lambda }}\|f\|_{L^{1}(\mathbb {R} )}}$$

für alle ${\displaystyle \lambda >0}$ und alle Funktionen ${\displaystyle f\in L^{1}(\mathbb {R} )}$ gilt.

Beziehung zu den Kramers-Kronig-Relationen

Die Kramers-Kronig-Relationen d​er Physik erhält m​an mit d​er formalen Identität (siehe Distribution (Mathematik))

${\displaystyle {\frac {1}{x}}=\lim \limits _{\varepsilon \to 0}{\frac {1}{x+\mathrm {i} \varepsilon }}=\lim \limits _{\varepsilon \to 0}{\frac {x}{x^{2}+\varepsilon ^{2}}}-\mathrm {i} \cdot \lim \limits _{\varepsilon \to 0}\,{\frac {\varepsilon }{x^{2}+\varepsilon ^{2}}}\,,}$

wobei der erste Teil bei der Integration über ${\displaystyle x}$ den Cauchy-Hauptwert CH von ${\displaystyle {\tfrac {1}{x}}}$ und der zweite Teil das ${\displaystyle \pi }$-fache der Dirac-Distribution ${\displaystyle \delta }$ ergibt.

Die Hilbert-Transformation findet dann Anwendung, wenn eine reelle Funktion von der reellen Achse ${\displaystyle \mathbb {R} }$ zu einer in der darüber liegenden komplexen Halbebene holomorphen Funktion fortgesetzt werden soll.

Literatur

• Karl Dirk Kammeyer: MATLAB in der Nachrichtentechnik. J. Schlembach Fachverlag, 2001, ISBN 3-935340-05-2.
• Bernd Girod, Rudolf Rabenstein, Alexander K. E. Stenger: Einführung in die Systemtheorie: Signale und Systeme in der Elektrotechnik und Informationstechnik. 4. Auflage. Teubner Verlag, Wiesbaden 2007, ISBN 978-3-8351-0176-0.

Weblinks

• Julius O. Smith III Analytic Signals and Hilbert Transform Filters, Stanford University (engl.)
• Python SciPy.org: Hilbert-Transformation mit Beispiel zur Hüllkurven-Berechnung (scipy.signal.hilbert)

Einzelnachweise

1. J. McFadden: An alternate proof of Nuttall's theorem on output cross-covariances. Hrsg.: IEEE Transactions on Information Theory. Band 11, 1965, S. 306–307.
2. S. Lawrence Marple: Computing the discrete-time analytic signal via FFT, IEEE Transactions on Signal Processing, Ausgabe 47, Nr. 9, September 1999, Seiten 2600–2603.