Negative Frequenz

Die negative Frequenz tritt als Komponente bei harmonischen Schwingungen auf, wenn die mathematische Beschreibung in der komplexen Zahlenebene mit komplexen Zahlen erfolgt. Physikalisch hat das Vorzeichen keine Bedeutung; es spezifiziert den rechts- bzw. linkswendigen Umlauf von Zeigern in der komplexen Zahlenebene.[1][2]

Der Begriff der negativen Frequenz spielt im Bereich der Signaltheorie und Signalverarbeitung eine Rolle, insbesondere bei technischen Modulationsverfahren.

Definition

Zeigerdiagramm zum sinus- bzw. cosinusförmigen Verlauf einer Schwingung

Eine Frequenz f gibt die Anzahl von Ereignissen innerhalb eines bestimmten Zeitraums an und ist üblicherweise eine positive Zahl. Eine harmonische Schwingung s_I(t) der Frequenz f und einer Amplitude A besitzt einen sinusförmigen Verlauf über die Zeit t:

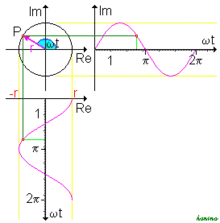
s_{\mathrm {I} }(t)=A\cdot \sin(2\pi f\cdot t)=A\cdot \sin(\omega \cdot t)

Der Ausdruck 2πf wird üblicherweise zur Kreisfrequenz ω zusammengefasst. Als Zeigerdiagramm in der komplexen Ebene lässt sich, wie in der nebenstehenden Abbildung dargestellt, beim Umlauf des Zeigers r auf der imaginären Achse der sinusförmige Verlauf über die Zeit t abbilden. Der auf der reellen Achse abgebildete cosinusförmige Verlauf ist dazu gleichwertig und stellt eine Phasenverschiebung von π/2 dar.

Die harmonische Schwingung lässt sich dazu gleichwertig als komplexe Schwingung über die Eulersche Identität angeben:

{\underline {s}}(t)=A\cdot \mathrm {e} ^{\mathrm {j} \omega \cdot t}

mit dem Realteil:

s_{\mathrm {R} }(t)=\mathrm {Re} \left\{A\cdot \mathrm {e} ^{\mathrm {j} \omega \cdot t}\right\}={\frac {1}{2}}\left(A\cdot \mathrm {e} ^{\mathrm {j} \omega \cdot t}+A\cdot \mathrm {e} ^{-\mathrm {j} \omega \cdot t}\right)

und dem Imaginärteil:

s_{\mathrm {I} }(t)=\mathrm {Im} \left\{A\cdot \mathrm {e} ^{\mathrm {j} \omega \cdot t}\right\}={\frac {1}{2\mathrm {j} }}\left(A\cdot \mathrm {e} ^{\mathrm {j} \omega \cdot t}-A\cdot \mathrm {e} ^{-\mathrm {j} \omega \cdot t}\right)

Die jeweils geklammerten Ausdrücke stellen dazu gleichwertig die Schwingung als eine Summe einer positiven und einer negativen Frequenz dar. Grafisch im Zeigerdiagramm ist der Ausdruck durch zwei gegensinnig umlaufende Zeiger darstellbar, die Umlaufrichtung der Zeiger wird durch das Vorzeichen der Frequenz bestimmt.

Anwendungen

Die Unterscheidung in positive und negative Frequenzen besitzt insbesondere bei technischen Modulationsverfahren und der Signalverarbeitung eine Bedeutung. Wird ein Signal als Informationsträger durch die Amplitudenmodulation aus der Basisbandlage zwecks Übertragung in einen höheren Frequenzbereich moduliert, ergeben sich durch die positiven bzw. negativen Frequenzen des Signals ein oberes bzw. unteres Seitenband. Diese beiden Seitenbänder tragen beide die gleiche Signalinformation des Basisbandes.

Eine Möglichkeit, eines der beiden Seitenbänder zu unterdrücken, besteht darin, mittels der Hilbert-Transformation aus dem reellen Signal ein analytisches Signal zu bilden. Ein analytisches Signal ist ein komplexes Signal, dessen negative Frequenzanteile gleich 0 sind und nur aus positiven Frequenzen besteht.

Einzelnachweise

Behandlung der komplexen Darstellung von Wellen (PDF; 728 kB) - Negative Frequenzen und komplexe Felder
Christof Pölczer: Digitale Signalverarbeitung - Komplexe Zeigerrechnung. (pdf) Abgerufen am 5. Februar 2018 (Vorlesungsskript).

Literatur

Rudolf Mäusl, Jürgen Göbel: Analoge und digitale Modulationsverfahren - Basisband und Trägermodulationen. 1. Auflage. Hüthig, 2002, ISBN 3-7785-2886-6.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Behandlung der komplexen Darstellung von Wellen (PDF; 728 kB) - Negative Frequenzen und komplexe Felder

[2] Christof Pölczer: Digitale Signalverarbeitung - Komplexe Zeigerrechnung. (pdf) Abgerufen am 5. Februar 2018 (Vorlesungsskript).