Partikelgrößenverteilung

Der Begriff der Partikelgrößenverteilung ist der Statistik entlehnt. Dort werden Häufigkeiten und Häufigkeitsverteilungen eines beliebigen Merkmals, z. B. Würfelaugen, Fertigungstoleranzen etc., betrachtet. Im Bereich der Partikeltechnologie und der Partikelmesstechnik bzw. der Dispersitätsanalyse wird als Merkmal der Äquivalentdurchmesser eines Partikels gewählt. Aus der allgemeinen Häufigkeitsverteilung der Statistik resultiert somit die Partikelgrößenverteilung. Diese wird häufig auch als Korngrößenverteilung bezeichnet.

Definitionen

Die Partikel (disperse Phase) innerhalb eines umgebenden Mediums (kontinuierliche Phase), d. h. Körner, Tropfen oder Blasen, werden mit Hilfe eines zu messenden Äquivalentdurchmessers unterschieden und entsprechend ihrer Größe in ausgewählte Klassen eingeordnet. Zur Darstellung einer Partikelgrößenverteilung werden die Mengenanteile bestimmt, mit denen die jeweiligen Partikelklassen an der dispersen Phase beteiligt sind.

Es werden unterschiedliche Mengenarten verwendet. Werden die Partikel gezählt, so ist die Mengenart die Anzahl. Bei Wägungen hingegen ist es die Masse bzw. bei homogener Dichte ρ das Volumen. Weitere leiten sich aus Längen, Projektions- und Oberflächen her. Man unterscheidet:

Mengenart	Index r	Messverfahren (Beispiele)
Anzahl	0	elektrische Mobilitätsanalyse
Länge	1	Sedimentationsanalyse
Fläche	2	Extinktionsmessung
Volumen (Masse)	3	Siebanalyse

Zur graphischen Darstellung wird ein normiertes Mengenmaß verwendet. Die Normierung ist erforderlich, um die Abhängigkeit der Mengenanteile von der verwendeten Gesamtmenge zu eliminieren. Auf diese Art ist beispielsweise das Ergebnis einer ersten Wägung von 100 g Gesamtmasse mit dem Ergebnis einer Wägung von 1 kg Gesamtmasse vergleichbar.

Es werden zwei Mengenmaße unterschieden:

Summenverteilung Q_r
Dichteverteilung q_r

Die Bezeichnungen Q_r bzw. q_r sind die Formelzeichen des Begriffs Quantil. Der Index r bezeichnet die Mengenart gemäß obiger Tabelle.

Generell werden bei der graphischen Darstellung einer Partikelgrößenverteilung der Äquivalentdurchmesser x auf der Abszisse und das Mengenmaß Q_r bzw. q_r auf der Ordinate aufgetragen.

Summenverteilungskurve

Die Summenverteilungskurve Q_r(x) gibt die normierte Menge aller Partikel mit einem Äquivalentdurchmesser kleiner gleich x an. Im Folgenden werden Summenverteilungen der beiden gebräuchlichsten Mengenarten explizit definiert:

Partikelzahl (r = 0)

Sei N_i die Zahl aller untersuchten Partikel mit einem Durchmesser x kleiner oder gleich dem betrachteten Durchmesser x_i sowie N die Gesamtzahl aller untersuchten Partikel. Dann ist

Q_{0}(x_{i})={\frac {N_{i}}{N}}

Partikelmasse (r = 3)

Sei m_i die Masse aller untersuchten Partikel mit einem Durchmesser x kleiner oder gleich dem betrachteten Durchmesser x_i sowie m die Gesamtmasse aller untersuchten Partikel. Dann ist

Q_{3}(x_{i})={\frac {m_{i}}{m}}

Für die anderen Mengenarten wird analog vorgegangen.

Beispiel: Eine Wägung ergibt, dass 20 g einer Probe der Gesamtmasse 100 g durch ein Sieb mit einer Maschenweite von 1 mm gefallen und damit kleiner als 1 mm sind. Daher ist

Q_{3}(1\,\mathrm {mm} )={\frac {20\,\mathrm {g} }{100\,\mathrm {g} }}=0{,}2

Aufgrund der Normierung, d. h. der jeweiligen Division durch die Gesamtmenge, gilt

$Q_{r}(x=0)=Q_{r}(x=x_{\mathrm {min} })=0$
$Q_{r}(x=\infty )=Q_{r}(x=x_{\mathrm {max} })=1$

Das Mengenmaß Q_r ist stets dimensionslos.

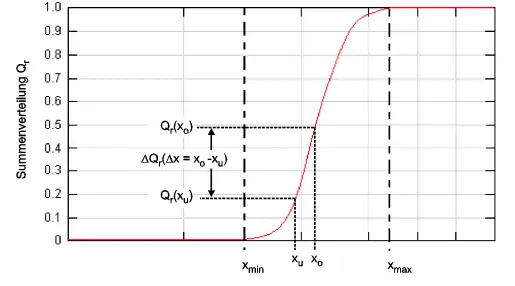
Das folgende Diagramm zeigt eine typische Summenverteilungskurve mit den minimalen und maximalen Äquivalentdurchmessern x_min bzw. x_max. Die diskreten Elemente der Summenverteilung werden hierbei über den einzelnen Klassenobergrenzen x_o,i aufgetragen:

Summenverteilungskurve \math{Q_r}

Dichteverteilungen

Lineare Dichteverteilungskurve

Wird die Differenz zwischen den Mengenanteilen Q_r der Äquivalentdurchmesser x_u,i (untere Grenze der Klasse i) und x_o,i (obere Grenze der Klasse i) gebildet, dann gilt:

\Delta Q_{r}(x_{u,i},x_{o,i})=Q_{r}(x_{o,i})-Q_{r}(x_{u,i})

Damit ist die diskrete Dichteverteilung q_r(x) wie folgt definiert:

q_{r}(x_{u,i},x_{o,i})={\frac {\Delta Q_{r}(x_{u,i},x_{o,i})}{\Delta x_{i}}}

Hierbei gilt für die Breite der Klasse i:

\Delta x_{i}=x_{o,i}-x_{u,i}

Im Falle einer differenzierbaren Summenverteilung Q_r(x) ist die Dichteverteilung die 1. Ableitung von Q_r(x):

q_{r}(x)={\frac {dQ_{r}(x)}{dx}}

Die lineare Dichteverteilung q_r(x) hat – vorausgesetzt x ist ein Äquivalentdurchmesser – die Einheit [m⁻¹]. Das folgende Diagramm zeigt eine typische Dichteverteilungskurve:

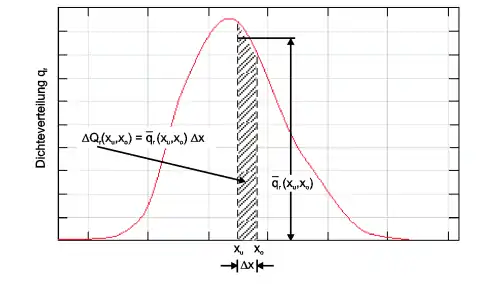
lineare Dichteverteilungskurve q_r

Die markierte Fläche ist der im Intervall Δx_i = x_o,i – x_u,i enthaltene Mengenanteil ΔQ_r der Partikel, deren Größe bzw. Äquivalentdurchmesser x zwischen x_u,i und x_o,i liegt. Aufgrund der Normierung der Summenverteilung Q_r ist die Fläche unterhalb der Dichteverteilungskurve gleich 1:

\int _{x_{\mathrm {min} }}^{x_{\mathrm {max} }}q_{r}(x)\;dx=Q_{r}(x_{\mathrm {max} })-Q(x_{\mathrm {min} })=1

In der Praxis wird man es hingegen in der Regel mit diskreten Werten, das heißt einzelnen Werten, der Dichteverteilung zu tun haben. Die Dichteverteilung als Funktion ist nicht explizit bekannt. Es werden dann mehrere Möglichkeiten der Auftragung verwendet:

Histogramm:

Die Dichteverteilung wird im Intervall Δx_i als konstant angenommen. Als Konsequenz ergibt sich eine rechteckige Fläche:

\Delta Q_{r,i}=q_{r}(x_{u,i},x_{o,i})\cdot \Delta x_{i}

Polygonzug:

Der Wert der Dichteverteilung q_r für das Intervall (x_u,i,x_o,i) wird am Ort der arithmetischen Klassenmitte aufgetragen, d. h. bei x_m,a = (x_o,i + x_u,i)/2. Die sich ergebenden Datenpunkte werden als Näherung linear verbunden.

Spline-Interpolation:

Wie beim Polygonzug wird der Wert der Dichteverteilung am Ort der arithmetischen Klassenmitte aufgetragen. Die Werte werden anschließend durch eine polynomiale Näherungsfunktion (Spline) verbunden. Dabei ist zu beachten, dass die auf diese Weise interpolierten Werte mathematischen und nicht physikalischen Ursprungs sind.

Histogramm
Polygonzug
Spline

Die Dichteverteilung q_r(x) zeigt sehr häufig die Form einer Gaußschen Glocke. Weist die Verteilung lediglich ein Maximum auf, so spricht man von einer monomodalen Verteilung. Bei zwei Maxima ist die Verteilung bimodal. Der Abszissenwert des größten Maximums wird als Modalwert bezeichnet.

Dichtefunktion der Partikelanzahlkonzentration

Im Bereich der atmosphärischen Aerosole wird anstatt der reinen Dichtefunktion die Dichtefunktion der Partikelanzahlkonzentration verwendet. Hierfür wird die Dichteverteilung mit der gemessenen Partikelanzahlkonzentration multipliziert.

q_{0}^{*}(x)=q_{0}(x)\cdot c_{n}

Der Vorteil dieser Darstellungsform ist die direkte Vergleichbarkeit von Partikelgrößenverteilung und Partikelanzahlkonzentration von Aerosolen.

Logarithmische Dichteverteilung (Transformierte Dichteverteilung)

Die Darstellung einer linearen Dichteverteilung q_r ist unpraktisch, wenn sich der Bereich der vorliegenden Äquivalentdurchmesser über mehr als eine Dekade erstreckt. Man spricht in diesem Zusammenhang von einer breiten Verteilung. Für diese Fälle ist es angebracht, eine logarithmisch geteilte Abszisse zu verwenden, da der Überblick dann wesentlich leichter fällt. Die logarithmische Dichteverteilung wird mit q_r* oder q_r,log gekennzeichnet. Der Wert der Dichteverteilung q_r* für das Intervall (x_u,i,x_o,i) wird am Ort der geometrischen Klassenmitte aufgetragen, d. h. bei:

x_{m,i,g}={\sqrt[{2}]{x_{o,i}\cdot x_{u,i}}}

In der Praxis hat sich die logarithmische Auftragung gegenüber der linearen Auftragung oftmals als vorteilhaft herausgestellt. Das folgende Diagramm zeigt eine logarithmische Auftragung einer engen Verteilung.

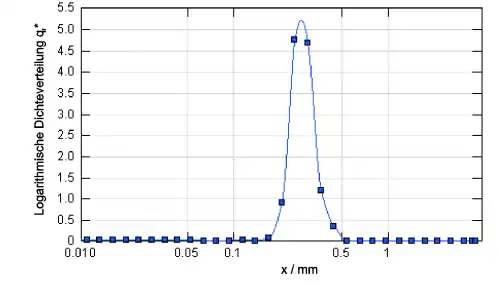
Logarithmische Dichteverteilungskurve q_r*

Mathematisch betrachtet handelt es sich bei der logarithmischen Auftragung um eine Substitution der Abszisse. Es gilt ganz allgemein:

q_{r}^{*}(s)=q_{r}(x)\cdot {\frac {\mathrm {d} x}{\mathrm {d} s}}

und mit s = lg x = (ln x)/2,3026 erhält man für die Umrechnung

q_{r}^{*}(\lg \,x)=2{,}3026\cdot x\cdot q_{r}(x)

Es muss betont werden, dass die logarithmische Substitution der Abszisse zu einer Änderung des Kurvenverlaufs führt, d. h. unter anderem, dass sich der Modalwert verschiebt. Die Normierungsbedingung bleibt dagegen stets erfüllt.

Literatur

DIN 66143 Darstellung von Korn-(Teilchen-)größenverteilungen – Potenznetz. 1974.
DIN 66144 Darstellung von Korn-(Teilchen-)größenverteilungen – Logarithmisches Normalverteilungsnetz. 1974.
DIN 66145 Darstellung von Korn-(Teilchen-)größenverteilungen – RRSB-Netz. 1976.
DIN 66160 Messen disperser Systeme, Begriffe.
DIN 66161 Partikelgrößenanalyse, Formelzeichen, Einheiten.
DIN ISO 9276-1 Darstellung der Ergebnisse von Partikelgrößenanalysen. Teil 1: Grafische Darstellung.
Matthias Stieß: Mechanische Verfahrenstechnik. Band 1. 2., neubearbeitete Auflage. Springer, Berlin u. a. 1995, ISBN 3-540-59413-2 (3., vollständig neu bearbeitete Auflage, als: Mechanische Verfahrenstechnik. Band 1: Partikeltechnologie. ebenda 2009 (erschienen 2008), ISBN 978-3-540-32551-2).
Albrecht F. Braun: Die genetische Deutung natürlicher Haufwerke mit Hilfe des doppeltlogarithmischen Körnungsnetzes nach ROSIN, RAMMLER und SPERLING (DIN 4190). In: Zeitschrift der Deutschen Geologischen Gesellschaft. Bd. 126, 1975, ISSN 0012-0189, S. 199–205, Abstract.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.