Gleichdick
Ein Gleichdick oder ein Bereich konstanter Breite ist anschaulich eine Figur, die überall gleich dick ist beziehungsweise die gleiche Breite besitzt. Den Rand einer solcher Figur bezeichnet man als Kurve konstanter Breite oder Orbiforme („Kreisförmige“).
Definition
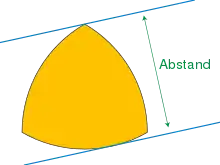
Die Breite einer Kurve ist definiert als der Abstand zwischen zwei parallelen Geraden, die die Kurve auf gegenüberliegenden Seiten berühren. Diese Geraden nennt man Stützgeraden. Kurven konstanter Breite sind diejenigen Kurven, bei denen sich für den Abstand dieser Geraden immer derselbe Wert ergibt, unabhängig davon, an welcher Stelle der Figur die Geraden angreifen.
Beispiele und Eigenschaften
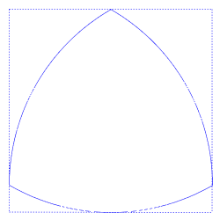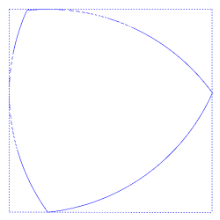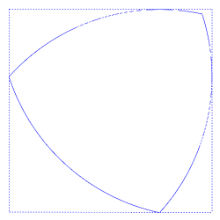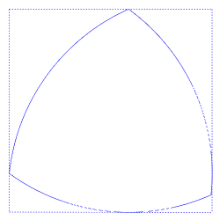
Das einfachste Beispiel für ein Gleichdick ist ein Kreis, dies ist der Trivialfall. Das einfachste nichttriviale aller Gleichdicke ist das Reuleaux-Dreieck. Es ist das Gleichdick mit der kleinsten Fläche, wohingegen der Kreis jenes mit der größten ist, dazwischen gibt es unendlich viele andere. Man kann mit Gleichdicken also Material sparen: Ein Kreis mit gleichem Durchmesser hat eine größere Fläche, eine zylindrische Walze mehr Volumen.
Ein Gleichdick muss nicht aus Kreisbögen gestaltet werden oder irgendwie symmetrisch sein. Allen Gleichdicken gemeinsam ist die konvexe Form.
Nach dem Satz von Barbier gilt für den Umfang eines beliebigen Gleichdicks der Breite :
Das heißt, der Umfang eines Gleichdicks ist gleich dem Umfang eines Kreises mit dem gleichen Durchmesser.
Bekannte Beispiele eines Gleichdicks sind die britischen 20- und 50-Pence-Münzen ab dem Ausgabedatum 1982 bzw. 1969 (bis laufend). Ihre siebeneckige Form mit gerundeten Seiten führt dazu, dass im Vergleich zum Kreis mit gleichem Durchmesser Material gespart wird. Der Münzdurchmesser kann (bis auf einen Fehler durch die Eckenabrundung) zwischen parallelen Backen oder einem Münzeinwurfschlitz in jeder beliebigen Richtung der Münze bestimmt werden. Beim abrollenden Drehen zwischen den Fingern können die Ecken ertastet werden. Beim ausreichend schnellen Rollen der Münzen können diese von einer harten Bahn etwas abheben oder springen.
Ein Bohrer mit dem Querschnitt eines Reuleaux-Dreiecks kann zum Bohren von „eckigen“ Löchern genutzt werden. Erfunden hat diesen Bohrer, der beinahe viereckige Löcher erzeugt, der britische Ingenieur Harry James Watt 1914 (US-Patent 1241175 und folgende).
Kreise haben eine konstante Breite, die ihrem Durchmesser entspricht. Quadrate haben keine konstante Breite: Geraden parallel zu zwei gegenüberliegenden Seiten des Quadrats liegen näher beieinander als Geraden parallel zu einer Diagonalen. Allgemein kann kein Polygon eine konstante Breite haben. Es gibt jedoch auch andere Formen mit konstanter Breite. Ein Standardbeispiel ist das Reuleaux-Dreieck, der Schnittpunkt von drei Kreisen, von denen jeder dort zentriert ist, wo sich die anderen beiden Kreise kreuzen. Seine Grenzkurve besteht aus drei Bögen dieser Kreise, die sich in Winkeln von 120° treffen, so dass sie nicht glatt ist, und tatsächlich sind diese Winkel die schärfsten, die für jede Kurve konstanter Breite möglich sind. Andere Kurven mit konstanter Breite können glatt, aber nicht kreisförmig sein und nicht einmal Kreisbögen in ihrer Begrenzung aufweisen. Zum Beispiel bilden die Nullstellen des folgenden Polynoms eine nicht kreisförmige glatte algebraische Kurve konstanter Breite:
Der Grad 8 ist der minimal mögliche Grad für ein Polynom, das eine nicht kreisförmige Kurve konstanter Breite definiert.[1]
Die dreidimensionale Verallgemeinerung
Ein räumliches Gleichdick ist ein konvexer Körper konstanter Breite: ein Körper ohne Einbuchtungen, der in jeder Lage innerhalb eines geeigneten Würfels stets alle sechs Seitenflächen berührt: In welcher Orientierung ein solcher Körper auch zwischen zwei parallele Platten eingespannt wird, immer sind die beiden Platten exakt gleich weit voneinander entfernt.
Ein einfaches nichttriviales räumliches Gleichdick ist der Rotationskörper, der durch Drehung eines Reuleaux-Dreiecks um eine seiner Symmetrieachsen entsteht. Aber auch alle anderen um eine Symmetrieachse rotierten Reuleaux-Polygone sind Körper konstanter Breite. Damit gibt es unendlich viele verschiedene räumliche Gleichdicke derselben konstanten Breite. Die Verhältniszahl zwischen Inkreis und Umkreis wird nach dem Trilobular auch als Trilobularität bezeichnet.[2]
Entgegen der intuitiven Annahme, das Reuleaux-Tetraeder sei ebenfalls von konstanter Breite, handelt es sich bei diesem Körper um kein Gleichdick. Jedoch lassen sich auf dessen Grundlage räumliche Gleichdicke konstruieren, die keine Rotationskörper sind, die beiden Meißner-Körper.
Auftreten von Gleichdicken in der Produktion
Beim (Umfangs-)Walzen von zylindrischen oder zylinderähnlichen Werkstücken wie Schrauben oder Steckkontakten ist es durch Toleranzen eher die Regel als die Ausnahme, dass statt Zylindern Gleichdicke entstehen. Oft ist dies unkritisch, jedoch kommt es zu Problemen, wenn ein Formschluss (bspw. für Dichtheit) benötigt wird.
Durch Messen zwischen zwei parallelen Flächen, etwa mit einem Messschieber oder einer maulförmigen Lehre, deren parallele Backen jeweils den nur an zwei Punkten gemessenen Durchmesser bestimmen, ist auf Grund der Definition des Gleichdicks kein Unterschied festzustellen. Wird jedoch ein Messinstrument mit drei etwa in Form eines gleichseitigen Dreiecks angeordneten Fühlstellen an ein Reuleaux-Dreieck herangeführt, sind je nach Verdrehlage des Werkstücks unterschiedliche Maße detektierbar. Realisiert werden können solche Messvorrichtungen mit einem Messschieber, dessen einem Backen ein M-förmiges Passstück (mit 120°-V- oder Rechteck-Nut) oder zwei Kreisscheiben in konstantem, geeignetem Abstand zueinander in Messrichtung aufgelegt wird.
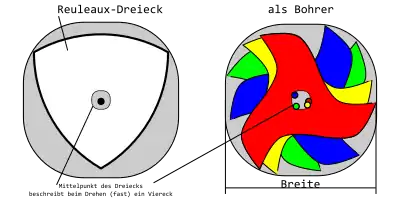
Anders als beim oben erwähnten Bohrer, der speziell zum Bohren eckiger Löcher erfunden wurde, kann ein ähnlicher Effekt auch ungewollt mit beliebigen Bohrern auftreten, wenn eine seitliche Bewegung der Bohrerspitze nicht ganz verhindert werden kann. Bohrer, die wegen großer Länge leichter ausweichen und nur zwei kurze Schneiden haben, neigen dazu, statt eines Kreises ruckweise ein Reuleaux-Dreieck herauszubohren. Bohrer mit drei Schneidkanten tendieren dazu, ein abgerundetes Viereck auszubohren (siehe nebenstehendes Bild) usw. Um unrunde Bohrlöcher zu verhindern, kann man zuerst das Loch mit etwa dem Viertel bis Drittel des End-Durchmessers vorbohren. Die Vorbohrung hilft, den folgenden Bohrer zentrisch zu führen. Bei Spiralbohrern führen die auf einem Zylinder liegenden Flächen hinter den spiraligen Schneiden ab einer gewissen Eindringtiefe den Bohrer und helfen so, eine unrunde Bohrung zu verhindern.
Schrauben, die in Blech oder Kunststoff selbstsichernde Eigenschaft gegen Verdrehen haben sollen, werden mitunter mit längs des Umfangs an drei Stellen leicht buckelig hervortretenden Schneideisen hergestellt, wofür die Kontur eines Reuleaux-Dreiecks gut geeignet ist. Typisch ist, dass diese Buckel als Dreifachhelix innen am umschriebenen Zylinder anliegen. Die Luft dieser oft selbstrillenden Schrauben gegenüber dem gebildeten zylindrischen Gewinde bietet Raum zur Aufnahme von Spänen. Insbesondere Kunststoff wird durch Aufweitung an den drei Dreieckspunkten günstig federnd verspannt.
Siehe auch
Literatur
- Günter Aumann: Kreisgeometrie: Eine elementare Einführung. Springer, 2015, ISBN 978-3-662-45306-3, S. 207–230
- Hans Rademacher, Otto Toeplitz: Von Zahlen und Figuren: Proben Mathematischen Denkens für Liebhaber der Mathematik. Springer, 2. Auflage 1933, S. 137-150
- Christian Blatter: Über Kurven konstanter Breite. In: Elemente der Mathematik, Band 36, Heft 5, 1981, S. 105–114
- Karl Strubecker: Kurventheorie der Ebene und des Raumes. Walter de Gruyter (Sammlung Göschen Band 1113), 1955, S. 51–55
- Lucas Geitel: Gleichdicks – Figuren konstanter Breite. In: Alexander Blinne (Hrsg.), Matthias Müller (Hrsg.), Konrad Schöbel (Hrsg.): Was wäre die Mathematik ohne die Wurzel?: Die schönsten Artikel aus 50 Jahren der Zeitschrift Die Wurzel. Springer, 2017, ISBN 9783658147594, S. 263–268
- Julian Havil: Curves for the Mathematically Curious: An Anthology of the Unpredictable, Historical, Beautiful, and Romantic. Princeton University Press, 2019, ISBN 9780691197784, S. 104–125
Weblinks
Einzelnachweise
- Stanley Rabinowitz: A Polynomial Curve of Constant Width
- Thomas Andreas Peter: Charakterisierung von Osteosyntheseplatten (PDF; 13 MB), Dissertation an der ETH Zürich zum Doktor der technischen Wissenschaften, 2001, S. 139 f.