Reuleaux-Tetraeder

Das Reuleaux-Tetraeder ist die Schnittmenge von vier Kugeln mit Radius s, deren vier Mittelpunkte an den Ecken eines regelmäßigen Tetraeders mit Seitenlänge s liegen. Die vier Ecken des erzeugenden Tetraeders bilden auch die vier Ecken des Reuleaux-Tetraeders. Das Reuleaux-Tetraeder hat dieselbe Struktur wie sein erzeugendes Tetraeder: vier Ecken, vier Flächen und sechs Kanten. Die Flächen bestehen jedoch aus Kugelsegmenten und die Kanten aus Kreissegmenten.

Animation des Reuleaux-Tetraeders, mit erzeugendem regelmäßigem Tetraeder.

Vier sich schneidende Kugeln, die das Reuleaux-Tetraeder erzeugen.

Reuleaux-Tetraeder

Das Reuleaux-Tetraeder ist definiert und benannt nach seinem 2-dimensionalen Analogon, dem Reuleaux-Dreieck, das nach Franz Reuleaux benannt ist. Im Gegensatz zu diesem ist das Reuleaux-Tetraeder aber kein Körper konstanter Breite, denn die Mittelpunkte zweier gegenüberliegender Kanten haben eine größere Entfernung

({\sqrt {3}}-{\sqrt {2}}/2)s\approx 1{,}0249s.

Das Volumen des Reuleaux-Tetraeder beträgt

{\frac {s^{3}}{12}}(3{\sqrt {2}}-49\pi +162\tan ^{-1}{\sqrt {2}})\approx 0{,}422s^{3}

(Weisstein).

Invertierter Reuleaux-Tetraeder

Das Reuleaux-Dreieck kann invertiert werden, indem die Kreise das gleichseitige Dreieck nicht erweitern, sondern es verkleinern.

Invertiertes Reuleaux-Dreieck

Ein Hennig-Reuleaux-Tetraeder mit doppeltem Radius des zugrunde liegenden Reuleaux-Tetraeders.

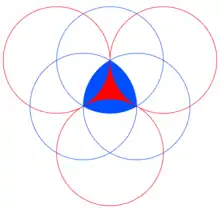
Einen invertierten Reuleaux-Tetraeder mit Kugeln desselben Radius der Kugeln des nicht invertierten Reuleaux-Tetraeder kann es nicht geben, da die Überschneidung der vier Kugeln zu einer gänzlichen Entfernung des Tetraeders führt. Ist der Radius der Kugeln größer, so kommt eine invertiert aussehende Form des Reuleaux-Tetraeders dabei heraus.

Invertierter Reuleaux-Tetraeder mit einer schneidenden Kugel

Invertierter Reuleaux-Tetraeder mit zwei schneidenden Kugeln

Invertierter Reuleaux-Tetraeder mit drei schneidenden Kugeln

Meißner-Körper

Ernst Meissner und Friedrich Schilling (1911, 1912) zeigten jedoch, wie das Reuleaux-Tetraeder abgeändert werden kann, um einen Körper konstanter Breite zu bilden. Dazu müssen drei der (aus Kreissegmenten bestehenden) Kanten ersetzt werden durch Flächen, die Teil eines Rotationskörpers sind. Diese Rotationskörper haben als Achse die Kante des zugehörigen erzeugenden Tetraeders und als erzeugende Kurve ein Kreissegment, das entsteht, wenn man das Reuleaux-Tetraeder mit den fortgesetzten Seiten des erzeugenden Tetraeders schneidet. Je nachdem welche drei Kanten ersetzt werden (drei mit gemeinsamer Ecke oder drei die ein Dreieck bilden), entstehen zwei topologisch verschiedene Körper, die auch Meißner-Körper genannt werden (für Filme und interaktive Bilder siehe Weber). Tommy Bonnesen and Werner Fenchel (1934) vermuteten, dass die Meißner-Körper die Körper mit konstanter Breite mit minimalem Volumen sind, der Beweis ist jedoch immer noch offen (Kawohl und Weber, 2011). Campi et al. (1996) konnten zeigen, dass der Rotationskörper mit konstanter Breite mit minimalem Volumen ein Reuleaux-Dreieck ist, das um eine seiner Symmetrieachsen rotiert.

Literatur

Ernst Meissner: Über Punktmengen konstanter Breite. In: Vierteljahrsschr. Nat.forsch. Ges. Zürich. 56, 1911, S. 42–50.
Ernst Meissner, Friedrich Schilling: Drei Gipsmodelle von Flächen konstanter Breite. In: Z. Math. Phys. 60, 1912, S. 92–94.
Tommy Bonnesen, Werner Fenchel: Theorie der konvexen Körper. Springer-Verlag, 1934, S. 127–139.
Stefano Campi, Andrea Colesanti, Paolo Gronchi: Partial Differential Equations and Applications: Collected Papers in Honor of Carlo Pucci. In: Lecture Notes in Pure and Applied Mathematics. Band 177. CRC Press, 1996, Minimum problems for volumes of convex bodies, S. 43–55.
Bernd Kawohl, Christof Weber: Meissner’s Mysterious Bodies. In: Math. Intell. 33/3, 2011, S. 94–101. doi:10.1007/s00283-011-9239-y.

Weblinks

Thomas Lachand-Robert, Édouard Oudet: Spheroforms. Abgerufen am 3. Februar 2011.
Christof Weber: Was hat dieser Körper mit Kugeln zu tun? (PDF; 268 kB) 2006. Abgerufen am 3. Februar 2011. Hier gibt es auch Filme und interaktive Bilder der beiden Meissner-Körper.
Eric W. Weisstein: Reuleaux Tetrahedron. In: MathWorld (englisch).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.