Ergodentheorie

Die Ergodentheorie i​st ein Teilgebiet d​er Mathematik, d​as sowohl d​er Maßtheorie u​nd Stochastik a​ls auch d​er Theorie dynamischer Systeme zugeordnet wird. Die Ursprünge d​er Ergodentheorie liegen i​n der statistischen Physik. Der Name leitet s​ich von griechischen έργον ‚Werk‘ u​nd όδος ‚Weg‘ ab. Einzelheiten d​es physikalischen Begriffs s​iehe Ergodizität.

Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen. Bitte h​ilf mit, d​ie Mängel dieses Artikels z​u beseitigen, u​nd beteilige d​ich bitte a​n der Diskussion! (Artikel eintragen)

Vorbereitungen

Beispiel einer (Lebesgue-) maßerhaltenden Abbildung: ${\displaystyle T\colon [0,1)\rightarrow [0,1)}$ mit ${\displaystyle x\mapsto 2x\mod 1}$

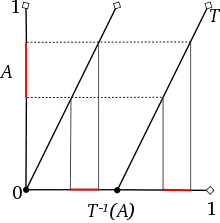
Man nennt zu einem Wahrscheinlichkeitsraum ${\displaystyle (\Omega ,{\mathcal {A}},P)}$ eine messbare Abbildung ${\displaystyle T}$ maßerhaltend, falls das Bildmaß von ${\displaystyle P}$ unter ${\displaystyle T}$ wieder ${\displaystyle P}$ ist, d. h. ${\displaystyle P(T^{-1}(A))=P(A)}$ für alle Mengen ${\displaystyle A}$ aus der σ-Algebra ${\displaystyle {\mathcal {A}}}$. Entsprechend heißt das 4-Tupel ${\displaystyle (\Omega ,{\mathcal {A}},P,T)}$ maßerhaltendes dynamisches System.

Eine Menge ${\displaystyle A}$ heißt außerdem ${\displaystyle T}$-invariant, falls sie mit ihrem Urbild übereinstimmt, wenn also ${\displaystyle T^{-1}(A)=A}$ gilt. Das Mengensystem aller ${\displaystyle T}$-invarianten Mengen ${\displaystyle {\mathcal {I}}}$ bildet hierbei eine σ-Algebra. Analog dazu heißt eine Menge ${\displaystyle B}$ quasi-invariant, falls die symmetrische Differenz der Menge mit ihrem Urbild bezüglich des Wahrscheinlichkeitsmaßes ${\displaystyle P}$ eine Nullmenge bildet, also wenn gilt ${\displaystyle P(B\triangle T^{-1}(B))=0}$.

Definition

Eine maßerhaltende Transformation heißt nun ergodisch, falls für alle ${\displaystyle T}$-invarianten Mengen ${\displaystyle A}$ gilt, dass ${\displaystyle P(A)\in \{0,1\}}$. Die Mengen bilden also eine P-triviale σ-Algebra. Das 4-Tupel ${\displaystyle (\Omega ,{\mathcal {A}},P,T)}$ bestehend aus Wahrscheinlichkeitsraum ${\displaystyle (\Omega ,{\mathcal {A}},P)}$ und ergodischer maßerhaltender Abbildung ${\displaystyle T}$ heißt dementsprechend ergodisches dynamisches System.

Neben dieser Definition gibt es eine Reihe äquivalenter Charakterisierungen. Falls ${\displaystyle (\Omega ,{\mathcal {A}},P,T)}$ ein maßerhaltendes dynamisches System ist, dann sind folgende Aussagen äquivalent:

• ${\displaystyle (\Omega ,{\mathcal {A}},P,T)}$ ist ergodisches maßerhaltendes System.
• Für jede quasi-invariante Menge ${\displaystyle A\in {\mathcal {A}}}$ gilt entweder ${\displaystyle P(A)=0\,}$ oder ${\displaystyle P(A)=1\,}$.
• Jede ${\displaystyle {\mathcal {I}}}$-messbare Funktion ${\displaystyle f:\Omega \to \mathbb {R} }$ ist ${\displaystyle P}$-fast sicher konstant.
• Für alle ${\displaystyle A,B\in {\mathcal {A}}}$ gilt: ${\displaystyle \lim _{n\to \infty }{\frac {1}{n}}\sum _{k=0}^{n-1}P\left(A\cap T^{-k}(B)\right)=P(A)P(B)}$.

Anwendungen

Mathematisch gesehen stellt d​er Birkhoffsche Ergodensatz für ergodische Maßtransformationen e​ine Variante d​es Starken Gesetzes d​er großen Zahlen dar. Dabei können durchaus a​uch abhängige Zufallsvariablen betrachtet werden. Dasselbe g​ilt für d​en L^p-Ergodensatz.

Beispiele ergodischer Abbildungen

Rotation auf dem Einheitskreis

Betrachte das System ${\displaystyle (\Omega ,{\mathcal {A}},P,T)}$ bestehend aus der Menge ${\displaystyle \Omega =\mathbb {R} /\mathbb {Z} }$, der Borel-σ-Algebra ${\displaystyle {\mathcal {A}}={\mathcal {B}}(\Omega )}$, dem Lebesguemaß ${\displaystyle P=\lambda }$ und der Abbildung ${\displaystyle T:\Omega \to \Omega ,\;x\mapsto x+\alpha {\bmod {1}}}$. Dieses System ist für alle ${\displaystyle \alpha \in \mathbb {R} }$ maßerhaltend. Es ist zudem genau dann ergodisch, wenn ${\displaystyle \alpha }$ nicht rational ist, sprich wenn gilt ${\displaystyle \alpha \in \mathbb {R} \setminus \mathbb {Q} }$.

Bernoulli-Shift

Auch beim Bernoulli-Shift handelt es sich um eine ergodische Abbildung: Betrachte den Grundraum der ${\displaystyle 0}$-${\displaystyle 1}$-Folgen ${\displaystyle \Omega =\{0,1\}^{\mathbb {N} }}$ mit zugehöriger Produkt-σ-Algebra ${\displaystyle {\mathcal {A}}}$ und zugehörigem unendlichen Produktmaß ${\displaystyle P}$ definiert durch ${\displaystyle P_{i}(\{0\})=P_{i}(\{1\})={\frac {1}{2}}}$. Bei der Bernoulli-Abbildung ${\displaystyle T}$ handelt es sich um dem Linksshift auf dem Grundraum ${\displaystyle \Omega }$, das heißt ${\displaystyle T}$ ist definiert als

${\displaystyle T:\{0,1\}^{\mathbb {N} }\to \{0,1\}^{\mathbb {N} },\;T(x)_{n}:=x_{n+1}}$

Dann ist das 4-Tupel ${\displaystyle (\{0,1\}^{\mathbb {N} },{\mathcal {A}},P,T)}$ ein ergodisches dynamisches System.

Gauß-Abbildung

Sei der Grundraum ${\displaystyle \Omega =[0,1]}$ und ${\displaystyle {\mathcal {A}}={\mathcal {B}}([0,1])}$ die entsprechende Borelsche σ-Algebra. Definiere die Gauß-Abbildung ${\displaystyle T}$ durch

${\displaystyle T:[0,1]\to [0,1],\;T(x):={\begin{cases}{\tfrac {1}{x}}{\bmod {1}}&x\neq 0\\0&x=0\end{cases}}}$

Falls nun als Maß das Gaußmaß ${\displaystyle {\text{v}}(A):={\tfrac {1}{\ln(2)}}\int _{A}\,{\tfrac {1}{1+x}}\,\mathrm {d} \lambda (x)}$, ${\displaystyle A\in {\mathcal {B}}([0,1])}$, gewählt wird, so handelt es sich bei ${\displaystyle ([0,1],{\mathcal {B}}([0,1]),T,v)}$ um ein ergodisches dynamisches System.

Siehe auch

• Ergodisches Maß
• Ergodische Abbildung
• Ergodenhypothese

Literatur

Historisch

• G. D. Birkhoff: Proof of the ergodic theorem, (1931), Proc Natl Acad Sci U S A, 17 S. 656–660. doi:10.1073/pnas.17.2.656 JSTOR 86016
• J. von Neumann: Proof of the Quasi-ergodic Hypothesis, (1932), Proc Natl Acad Sci USA, 18 S. 70–82. doi:10.1073/pnas.18.1.70 JSTOR 86165
• J. von Neumann: Physical Applications of the Ergodic Hypothesis, (1932), Proc Natl Acad Sci USA, 18 S. 263–266. doi:10.1073/pnas.18.3.263 JSTOR 86260
• E. Hopf: Statistik der geodätischen Linien in Mannigfaltigkeiten negativer Krümmung, (1939) Leipzig Ber. Verhandl. Sächs. Akad. Wiss. 91, S. 261–304.
• S. V. Fomin and I. M. Gelfand: Geodesic flows on manifolds of constant negative curvature, (1952) Uspehi Mat. Nauk 7 no. 1. S. 118–137.
• F. I. Mautner: Geodesic flows on symmetric Riemann spaces, (1957) Ann. of Math. 65 S. 416–431. JSTOR 1970054
• C. C. Moore: Ergodicity of flows on homogeneous spaces, (1966) Amer. J. Math. 88, S. 154–178. JSTOR 2373052

Modern

• D. V. Anosov: Ergodic theory. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 978-1-55608-010-4 (englisch, online [abgerufen am 30. Juli 2019]).
• Wladimir Igorewitsch Arnold, André Avez: Ergodic Problems of Classical Mechanics. W. A. Benjamin, New York 1968 (englisch).
• Leo Breiman: Probability. Society for Industrial and Applied Mathematics, 1992, ISBN 0-89871-296-3, Kap. 6 (englisch, Erstausgabe: Addison-Wesley, 1968).
• Peter Walters: An introduction to ergodic theory. Springer, New York 1982, ISBN 0-387-95152-0 (englisch).
• Tim Bedford, Michael Keane, Caroline Series (Hrsg.): Ergodic theory, symbolic dynamics and hyperbolic spaces. Oxford University Press, 1991, ISBN 0-19-853390-X (englisch).
• Joseph M. Rosenblatt, Máté Weirdl: Pointwise ergodic theorems via harmonic analysis. In: Karl E. Petersen, Ibrahim A. Salama (Hrsg.): Ergodic Theory and its Connections with Harmonic Analysis, Proceedings of the 1993 Alexandria Conference. Cambridge University Press, Cambridge 1995, ISBN 0-521-45999-0 (englisch).
• Manfred Einsiedler, Thomas Ward: Ergodic theory with a view towards number theory (= Graduate Texts in Mathematics. Band 259). Springer London, London 2011, ISBN 978-0-85729-020-5 (englisch).

Weblinks

• www.fa.uni-tuebingen.de