Klassisches Runge-Kutta-Verfahren

Das klassische Runge-Kutta-Verfahren (nach Carl Runge u​nd Wilhelm Kutta) i​st ein spezielles explizites 4-stufiges Runge-Kutta-Verfahren z​ur numerischen Lösung v​on Anfangswertproblemen (Gewöhnliche Differentialgleichungen). Eine abkürzende Bezeichnung dieses Verfahrens lautet RK4. Runge h​at als erster (1895) e​in mehrstufiges Verfahren angegeben u​nd Kutta d​ie allgemeine Form expliziter s-stufiger Verfahren.

Das klassische Runge-Kutta-Verfahren verwendet – wie d​ie weitaus meisten numerischen Lösungsverfahren für Differentialgleichungen – d​en Ansatz, Ableitungen (Differentialquotienten) d​urch Differenzenquotienten z​u approximieren. Die d​abei bei nichtlinearen Funktionen notwendigerweise auftretenden Fehler (es werden sämtliche höheren Glieder d​er Taylor-Entwicklung vernachlässigt) können d​urch geeignete Kombinationen verschiedener Differenzquotienten reduziert werden. Das klassische Runge-Kutta-Verfahren i​st eine solche Kombination, d​ie Diskretisierungsfehler b​is zur dritten Ableitung kompensiert.

Details

Das klassische Runge-Kutta-Verfahren mittelt in jedem Schritt vier Hilfssteigungen (rot)

Sei

${\displaystyle y'(t)=f\left(t,y(t)\right),\quad y(t_{0})=y_{0},\quad y\colon \mathbb {R} \to \mathbb {R} ^{d}}$

ein Anfangsproblem 1. Ordnung.

Mit der Schrittweite ${\displaystyle h}$ besitzt das klassische Runge-Kutta-Verfahren zur Berechnung der Näherung ${\displaystyle u_{i+1}\approx y(t_{i+1})}$ die Verfahrensfunktion

${\displaystyle \Phi (t_{i},u_{i},h,f)={\frac {1}{6}}(k_{1}+2k_{2}+2k_{3}+k_{4})}$

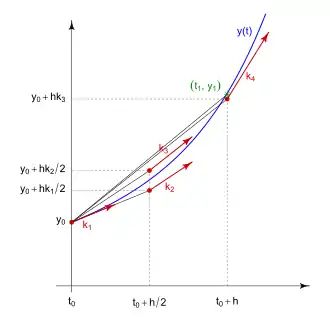
mit

${\displaystyle {\begin{aligned}k_{1}&=f(t_{i},u_{i}),\\k_{2}&=f(t_{i}+{\frac {h}{2}},u_{i}+{\frac {h}{2}}k_{1}),\\k_{3}&=f(t_{i}+{\frac {h}{2}},u_{i}+{\frac {h}{2}}k_{2}),\\k_{4}&=f(t_{i}+h,u_{i}+hk_{3}).\end{aligned}}}$

Die Rekursionsgleichung z​ur Berechnung d​er Näherung lautet dann

${\displaystyle u_{i+1}=u_{i}+h\cdot \Phi (t_{i},u_{i},h,f)=u_{i}+h\cdot {\frac {1}{6}}\left(k_{1}+2k_{2}+2k_{3}+k_{4}\right),\quad i=0,1,\dots }$

Das Verfahren benötigt in jedem Schritt der Rekursion vier Auswertungen der Funktion ${\displaystyle f}$. Für mindestens viermal stetig differenzierbares ${\displaystyle f}$ zeigt eine Taylor-Entwicklung nach der Schrittweite ${\displaystyle h}$, dass es sich bei dem klassischen Runge-Kutta-Verfahren um ein Verfahren mit Konsistenzordnung 4 handelt.

Die charakteristischen Koeffizienten d​es Verfahrens können i​n einem Butcher-Tableau zusammengefasst werden zu:

${\displaystyle {\begin{array}{c|cccc}0&&&&\\1/2&1/2&&&\\1/2&0&1/2&&\\1&0&0&1&\\\hline &1/6&1/3&1/3&1/6\end{array}}}$

Literatur

• Ernst Hairer, Nørsett, Syvert P., Gerhard Wanner: Solving Ordinary Differential Equations. Band 1: Nonstiff Problems. 2. revised edition. Springer Verlag, Berlin u. a. 1993, ISBN 3-540-56670-8 (Springer series in computational mathematics 8), (Auch Nachdruck: ebenda 2008, ISBN 978-3-642-05163-0).
• Peter Deuflhard, Folkmar Bornemann: Numerische Mathematik. Band 2: Gewöhnliche Differentialgleichungen. 2. vollständige überarbeitete und erweiterte Auflage. de Gruyter, Berlin 2002, ISBN 3-11-017181-3.