Dijkstra-Algorithmus
Der Algorithmus von Dijkstra (nach seinem Erfinder Edsger W. Dijkstra) ist ein Algorithmus aus der Klasse der Greedy-Algorithmen[1] und löst das Problem der kürzesten Pfade für einen gegebenen Startknoten. Er berechnet somit einen kürzesten Pfad zwischen dem gegebenen Startknoten und einem der (oder allen) übrigen Knoten in einem kantengewichteten Graphen (sofern dieser keine Negativkanten enthält).
Für unzusammenhängende ungerichtete Graphen ist der Abstand zu denjenigen Knoten unendlich, zu denen kein Pfad vom Startknoten aus existiert. Dasselbe gilt auch für gerichtete nicht stark zusammenhängende Graphen. Dabei wird der Abstand synonym auch als Entfernung, Kosten oder Gewicht bezeichnet.
Algorithmus
Informelle Darstellung
Die Grundidee des Algorithmus ist es, immer derjenigen Kante zu folgen, die den kürzesten Streckenabschnitt vom Startknoten aus verspricht. Andere Kanten werden erst dann verfolgt, wenn alle kürzeren Streckenabschnitte (auch über andere Knoten hinaus) beachtet wurden. Dieses Vorgehen gewährleistet, dass bei Erreichen eines Knotens kein kürzerer Pfad zu ihm existieren kann. Eine einmal berechnete Distanz zwischen dem Startknoten und einem besuchten Knoten wird gespeichert. Die aufsummierten Distanzen zu noch nicht abgearbeiteten Knoten können sich hingegen im Laufe des Algorithmus durchaus verändern, nämlich verringern. Dieses Vorgehen wird fortgesetzt, bis die Distanz des Zielknotens berechnet wurde (single-pair shortest path) oder die Distanzen aller Knoten zum Startknoten bekannt sind (single-source shortest path).
Der Algorithmus lässt sich durch die folgenden Schritte beschreiben. Es werden sowohl die kürzesten (aufsummierten) Wegstrecken als auch deren Knotenfolgen berechnet.
- Weise allen Knoten die beiden Eigenschaften (Attribute) „Distanz“ und „Vorgänger“ zu. Initialisiere die Distanz im Startknoten mit 0 und in allen anderen Knoten mit .
- Solange es noch unbesuchte Knoten gibt, wähle darunter denjenigen mit minimaler (aufsummierter) Distanz aus und
- Speichere, dass dieser Knoten schon besucht wurde.
- Berechne für alle noch unbesuchten Nachbarknoten die Gesamtdistanz über die Summe des jeweiligen Kantengewichtes und der bereits berechneten Distanz vom Startknoten zum aktuellen Knoten.
- Ist dieser Wert für einen Knoten kleiner als die dort gespeicherte Distanz, aktualisiere sie und setze den aktuellen Knoten als Vorgänger.
- Dieser Schritt wird auch als Update oder Relaxation/Relaxierung bezeichnet.
In dieser Form berechnet der Algorithmus ausgehend von einem Startknoten die kürzesten Wege zu allen anderen Knoten. Ist man dagegen nur an dem Weg zu einem ganz bestimmten Knoten interessiert, so kann man in Schritt (2) schon abbrechen, wenn der gesuchte Knoten der aktive ist.
Aufgrund der Eigenschaft, einmal festgelegte Distanzen zum Startknoten nicht mehr zu verändern, gehört der Dijkstra-Algorithmus zu den Greedy-Algorithmen, die in jedem Schritt die momentan aussichtsreichste Teillösung bevorzugen. Anders als manche andere Greedy-Algorithmen berechnet der Dijkstra-Algorithmus jedoch stets eine optimale Lösung. Diese Eigenschaft basiert auf der Annahme, dass die kürzesten Teilstrecken zwischen Knoten in einem Pfad zusammen die kürzeste Strecke auf diesem Pfad bilden. Unter der Voraussetzung positiver Kantengewichte ist die Annahme gültig, denn fände man nachträglich einen kürzeren Weg vom Startknoten zu einem Zielknoten, hätte man auch dessen kürzere Teilstrecke früher untersuchen müssen, um den Algorithmus korrekt durchzuführen. Dann hätte man aber über die kürzere Teilstrecke den Zielknoten früher gefunden als auf dem längeren Weg.
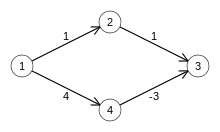
Die Annahme trifft jedoch nicht mehr zu, wenn der Graph negative Kantengewichte enthält. Dann kann jede Teilstrecke für sich zwar eine kürzeste Strecke zwischen den Endpunkten sein, man könnte jedoch über einen längeren Teilweg die Gesamtdistanz verbessern, wenn eine negative Kante die Weglänge wieder reduziert. Im Bild mit den Knoten 1, 2, 3 und 4 würde der Dijkstra-Algorithmus den kürzesten Weg von 1 nach 3 über 2 finden, da der Schritt zu 4 insgesamt schon länger ist als der gesamte obere Pfad. Die negative Kante bewirkt aber, dass der untere Pfad kürzer ist.
Algorithmus in Pseudocode
Die folgenden Zeilen Pseudocode beschreiben eine Funktion namens Dijkstra, die einen Graphen und einen Startknoten im Graphen als Eingabe erhält. Der Startknoten gibt den Knoten an, von dem aus die kürzesten Wege zu allen Knoten gesucht werden. Das Ergebnis ist eine Liste, die zu jedem Knoten v den Vorgängerknoten auf dem Weg vom Startknoten zu v angibt.
Der Graph besteht aus Knoten und gewichteten Kanten, wobei das Gewicht die Entfernung zwischen den Knoten darstellt. Existiert eine Kante zwischen zwei Knoten, so sind die Knoten jeweils Nachbarn. Der aktuell im Teilschritt betrachtete Knoten wird mit u bezeichnet und wird „Betrachtungsknoten“ genannt. Die möglichen, kommenden Nachbarknoten werden in der jeweiligen, kommenden Zwischenuntersuchung mit jeweils v als „Prüfknoten“ bezeichnet. Das Kantengewicht zwischen Betrachtungsknoten u und jeweiligen Prüfknoten v wird im Pseudocode als abstand_zwischen(u,v) angegeben.
Der Zahlenwert von abstand[v] enthält in dem Untersuchungszweig die jeweilige Gesamtentfernung, die die Teilentfernungen vom Startpunkt über mögliche Zwischenknoten und den aktuellen Knoten u bis zum nächsten zu untersuchenden Knoten v summiert.
Zunächst werden abhängig vom Graphen und Startknoten die Abstände und Vorgänger initialisiert. Dies geschieht in der Methode initialisiere. Der eigentliche Algorithmus verwendet eine Methode distanz_update, die ein Update der Abstände durchführt, falls ein kürzerer Weg gefunden wurde.
1 Funktion Dijkstra(Graph, Startknoten): 2 initialisiere(Graph,Startknoten,abstand[],vorgänger[],Q) 3 solange Q nicht leer: // Der eigentliche Algorithmus 4 u:= Knoten in Q mit kleinstem Wert in abstand[] 5 entferne u aus Q // für u ist der kürzeste Weg nun bestimmt 6 für jeden Nachbarn v von u: 7 falls v in Q: // falls noch nicht berechnet 8 distanz_update(u,v,abstand[],vorgänger[]) // prüfe Abstand vom Startknoten zu v 9 return vorgänger[]
Die Initialisierung setzt die Abstände auf unendlich und die Vorgänger als unbekannt. Nur der Startknoten hat die Distanz 0. Die Menge Q enthält die Knoten, zu denen noch kein kürzester Weg gefunden wurde.
1 Methode initialisiere(Graph,Startknoten,abstand[],vorgänger[],Q): 2 für jeden Knoten v in Graph: 3 abstand[v]:= unendlich 4 vorgänger[v]:= null 5 abstand[Startknoten]:= 0 6 Q:= Die Menge aller Knoten in Graph
Der Abstand vom Startknoten zum Knoten v verkürzt sich dann, wenn der Weg zu v über u kürzer als der bisher bekannte Weg ist. Entsprechend wird u zum Vorgänger von v auf dem kürzesten Weg.
1 Methode distanz_update(u,v,abstand[],vorgänger[]): 2 alternativ:= abstand[u] + abstand_zwischen(u, v) // Weglänge vom Startknoten nach v über u 3 falls alternativ < abstand[v]: 4 abstand[v]:= alternativ 5 vorgänger[v]:= u
Falls man nur am kürzesten Weg zwischen zwei Knoten interessiert ist, kann man den Algorithmus nach Zeile 5 der Dijkstra-Funktion abbrechen lassen, falls u = Zielknoten ist.
Den kürzesten Weg zu einem Zielknoten kann man nun durch Iteration über die vorgänger ermitteln:
1 Funktion erstelleKürzestenPfad(Zielknoten,vorgänger[]) 2 Weg[]:= [Zielknoten] 3 u:= Zielknoten 4 solange vorgänger[u] nicht null: // Der Vorgänger des Startknotens ist null 5 u:= vorgänger[u] 6 füge u am Anfang von Weg[] ein 7 return Weg[]
Implementierung
Knoten und Kanten zwischen Knoten lassen sich meistens durch Matrizen oder Zeigerstrukturen darstellen. Auch auf den Vorgänger eines Knotens kann ein Zeiger verweisen. Die Abstände der Knoten können in Feldern gespeichert werden.
Für eine effiziente Implementierung wird die Menge Q der Knoten, für die noch kein kürzester Weg gefunden wurde, durch eine Prioritätswarteschlange implementiert. Die aufwändige Initialisierung findet nur einmal statt, dafür sind die wiederholten Zugriffe auf Q effizienter. Als Schlüsselwert für den Knoten wird sein jeweiliger Abstand verwendet, der im Pseudocode mit abstand[v] angegeben ist. Verkürzt sich der Abstand, ist eine teilweise Neusortierung der Warteschlange nötig.
Als Datenstruktur bietet sich hierfür eine Entfernungstabelle oder eine Adjazenzmatrix an.
Programmierung
Das folgende Beispiel in der Programmiersprache C++ zeigt die Implementierung des Dijkstra-Algorithmus für einen ungerichteten Graphen, der als Adjazenzliste gespeichert wird. Bei der Ausführung des Programms wird die Funktion main verwendet, die einen kürzesten Weg auf der Konsole ausgibt.[2][3]
| Code-Schnipsel |
#include <iostream>
#include <vector>
#include <list>
#include <set>
#include <map>
#include <algorithm>
#include <iterator>
#include <string>
using namespace std;
const double maximumWeight = numeric_limits<double>::infinity(); // Konstante für das maximale Gewicht
// Datentyp, der die Nachbarknoten eines Knotens definiert
struct neighbor
{
int targetIndex; // Index des Zielknotens
string name; // Name des
double weight; // Gewicht der Kante
neighbor(int _target, string _name, double _weight) : targetIndex(_target), name(_name), weight(_weight) { }
};
// Berechnet die kürzesten Wege für den Knoten mit startIndex. Der gerichtete Graph wird als Adjazenzliste übergeben.
void ComputeShortestPathsByDijkstra(int startIndex, const vector<vector<neighbor>>& adjacencyList, vector<double>& minimumDistances, vector<int>& previousVertices, map<int, string>& vertexNames)
{
int numberOfVertices = adjacencyList.size(); // Anzahl der Knoten
// Initialisiert den Vektor für die kleinsten Abstände
minimumDistances.clear();
minimumDistances.resize(numberOfVertices, maximumWeight);
minimumDistances[startIndex] = 0;
// Initialisiert den Vektor für die Vorgängerknoten
previousVertices.clear();
previousVertices.resize(numberOfVertices, -1);
set<pair<double, int>> vertexQueue;
vertexQueue.insert(make_pair(minimumDistances[startIndex], startIndex)); // Warteschlange, die die Knoten des kürzesten Wegs enthält. Fügt den Startknoten hinzu.
vertexNames.insert(make_pair(startIndex, vertexNames[startIndex])); // Zuordnungstabelle, die die Knoten des kürzesten Wegs enthält. Fügt den Startknoten hinzu.
while (!vertexQueue.empty()) // Solange die Warteschlange nicht leer ist
{
double distance = vertexQueue.begin()->first; // Abstand
int index = vertexQueue.begin()->second;
vertexQueue.erase(vertexQueue.begin()); // Entfernt den ersten Knoten der Warteschlange
const vector<neighbor>& neighbors = adjacencyList[index];
// Diese for-Schleife durchläuft alle Nachbarn des Knoten mit index
for (vector<neighbor>::const_iterator neighborIterator = neighbors.begin(); neighborIterator != neighbors.end(); neighborIterator++)
{
int targetIndex = neighborIterator->targetIndex; // Index des Nachbarknotens
string name = neighborIterator->name; // Name des Nachbarknotens
double weight = neighborIterator->weight; // Abstand zum Nachbarknoten
double currentDistance = distance + weight; // Abstand vom Startknoten zum Knoten mit index
if (currentDistance < minimumDistances[targetIndex]) // Wenn der Abstand zum Nachbarknoten kleiner als die Länge des bisher kürzesten Wegs ist
{
vertexQueue.erase(make_pair(minimumDistances[targetIndex], targetIndex)); // Entfernt den Knoten aus der Warteschlange
vertexNames.erase(targetIndex); // Entfernt den Namen des Knotens aus der Zuordnungstabelle
minimumDistances[targetIndex] = currentDistance; // Speichert den Abstand vom Startknoten
previousVertices[targetIndex] = index; // Speichert den Index des Vorgängerknotens
vertexQueue.insert(make_pair(minimumDistances[targetIndex], targetIndex)); // Fügt den Knoten der Warteschlange hinzu
vertexNames.insert(make_pair(targetIndex, name)); // Fügt den Namen des Knotens der Zuordnungstabelle hinzu
}
}
}
}
// Gibt einen kürzesten Weg für den Knoten mit index zurück
list<string> GetShortestPathTo(int index, vector<int>& previousVertices, map<int, string>& vertexNames)
{
list<string> path;
for (; index != -1; index = previousVertices[index]) // Diese for-Schleife durchläuft den Weg
{
path.push_front(vertexNames[index]); // Fügt den Namen des Vorgängerknotens hinzu
}
return path;
}
// Hauptfunktion die das Programm ausführt
int main()
{
// Initialisiert die Adjazenzliste des gerichteten Graphen mit 6 Knoten
vector<vector<neighbor>> adjacencyList(6);
adjacencyList[0].push_back(neighbor(1, "Knoten 1", 7));
adjacencyList[0].push_back(neighbor(2, "Knoten 2", 9));
adjacencyList[0].push_back(neighbor(5, "Knoten 5", 14));
adjacencyList[1].push_back(neighbor(0, "Knoten 0", 7));
adjacencyList[1].push_back(neighbor(2, "Knoten 2", 10));
adjacencyList[1].push_back(neighbor(3, "Knoten 3", 15));
adjacencyList[2].push_back(neighbor(0, "Knoten 0", 9));
adjacencyList[2].push_back(neighbor(1, "Knoten 1", 10));
adjacencyList[2].push_back(neighbor(3, "Knoten 3", 11));
adjacencyList[2].push_back(neighbor(5, "Knoten 5", 2));
adjacencyList[3].push_back(neighbor(1, "Knoten 1", 15));
adjacencyList[3].push_back(neighbor(2, "Knoten 2", 11));
adjacencyList[3].push_back(neighbor(4, "Knoten 4", 6));
adjacencyList[4].push_back(neighbor(3, "Knoten 3", 6));
adjacencyList[4].push_back(neighbor(5, "Knoten 5", 9));
adjacencyList[5].push_back(neighbor(0, "Knoten 0", 14));
adjacencyList[5].push_back(neighbor(2, "Knoten 2", 2));
adjacencyList[5].push_back(neighbor(4, "Knoten 4", 9));
vector<double> minimumDistances; // Vektor für die kleinsten Abstände
vector<int> previousVertices; // Vektor für die Vorgängerknoten
map<int, string> vertexNames; // Vektor für die Namen der Knoten
ComputeShortestPathsByDijkstra(0, adjacencyList, minimumDistances, previousVertices, vertexNames); // Aufruf der Methode, die die kürzesten Wege für den Knoten 0 zurückgibt
cout << "Abstand von Knoten 0 nach Knoten 4: " << minimumDistances[4] << endl; // Ausgabe auf der Konsole
list<string> path = GetShortestPathTo(4, previousVertices, vertexNames); // Aufruf der Methode, die einen kürzesten Weg von Knoten 0 nach Knoten 4 zurückgibt
cout << "Kürzester Weg:"; // Ausgabe auf der Konsole
copy(path.begin(), path.end(), ostream_iterator<string>(cout, " ")); // Ausgabe auf der Konsole
cout << endl; // Ausgabe auf der Konsole
}
|
Beispiel mit bekanntem Zielknoten
Ein Beispiel für die Anwendung des Algorithmus von Dijkstra ist die Suche nach einem kürzesten Pfad auf einer Landkarte.[4] Im hier verwendeten Beispiel will man in der unten gezeigten Landkarte von Deutschland einen kürzesten Pfad von Frankfurt nach München finden.
Die Zahlen auf den Verbindungen zwischen zwei Städten geben jeweils die Entfernung zwischen den beiden durch die Kante verbundenen Städten an. Die Zahlen hinter den Städtenamen geben die ermittelte Distanz der Stadt zum Startknoten Frankfurt an, ∞ steht dabei für eine unbekannte Distanz. Die hellgrau unterlegten Knoten sind die Knoten, deren Abstand relaxiert wird (also verkürzt wird, falls eine kürzere Strecke gefunden wurde), die dunkelgrau unterlegten Knoten sind diejenigen, zu denen der kürzeste Weg von Frankfurt bereits bekannt ist.
Die Auswahl des nächsten Nachbarn erfolgt nach dem Prinzip einer Prioritätswarteschlange. Relaxierte Abstände erfordern daher eine Neusortierung.
- Beispiel
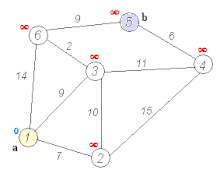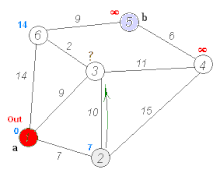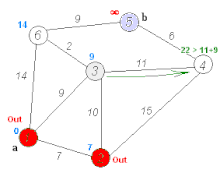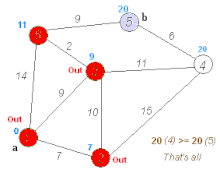
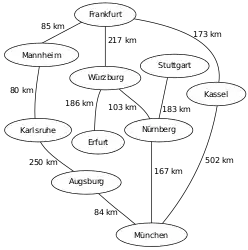Ausgangssituation: Nicht-initialisierter Graph mit Startknoten Frankfurt und Zielknoten München
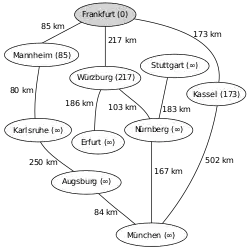Entfernungen vom Startknoten (Frankfurt) ermitteln (Relaxierung), Neusortieren der Prioritätswarteschlange Q (1. Mannheim, 2. Kassel, 3. Würzburg, …)
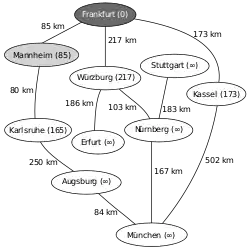Mannheim ist der nächstliegende Knoten, Relaxierung mit dem Nachbarknoten Karlsruhe, nächster Vorgänger von Karlsruhe ist nun Mannheim, Neusortieren von Q (1. Karlsruhe, 2. Kassel, 3. Würzburg, …)
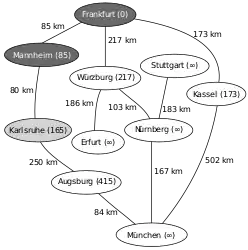Dem Startpunkt nächstliegender zu untersuchender Knoten laut Q ist nun Karlsruhe, Relaxierung mit Augsburg, Neusortieren von Q (1. Kassel, 2. Würzburg, 3. Augsburg, …)
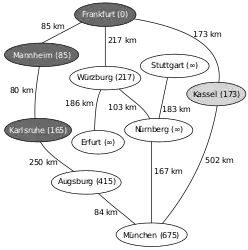Nächstliegender zu untersuchender Knoten ist nun Kassel, Relaxierung mit München, Neusortieren von Q (1. Würzburg, 2. Augsburg, 3. München, …)
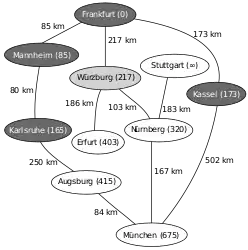Nächstliegender zu untersuchender Knoten ist nun Würzburg, Relaxierung mit Erfurt und Nürnberg, Neusortieren von Q (1. Nürnberg, 2. Erfurt, 3. Augsburg, 4. München, …)
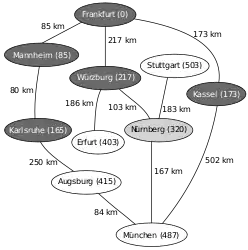Nächstliegender zu untersuchender Knoten ist nun Nürnberg, Relaxierung mit München und Stuttgart, Neusortieren von Q (1. Erfurt, 2. Augsburg, 3. München, 4. Stuttgart, …)
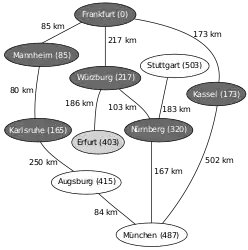Nächstliegender zu untersuchender Knoten ist nun Erfurt, Relaxierung mit niemandem, Neusortieren von Q (1. Augsburg, 2. München, 3. Stuttgart, …)
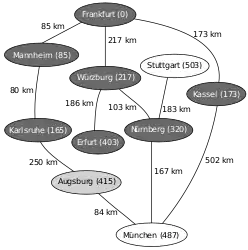Nächstliegender zu untersuchender Knoten ist nun Augsburg, Relaxierung mit München, Neusortieren von Q (1. München, 2. Stuttgart …)
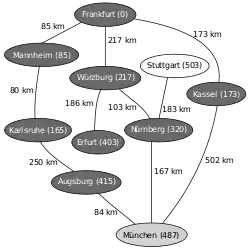Zielknoten soll untersucht werden: Kürzester Weg nach München ist nun bekannt; Rekonstruktion mittels erstelleKürzestenPfad(). Dieser ist: Frankfurt-Würzburg-Nürnberg-München.
Grundlegende Konzepte und Verwandtschaften
Ein alternativer Algorithmus zur Suche kürzester Pfade, der sich dagegen auf das Optimalitätsprinzip von Bellman stützt, ist der Floyd-Warshall-Algorithmus. Das Optimalitätsprinzip besagt, dass, wenn der kürzeste Pfad von A nach C über B führt, der Teilpfad A B auch der kürzeste Pfad von A nach B sein muss.
Ein weiterer alternativer Algorithmus ist der A*-Algorithmus, der den Algorithmus von Dijkstra um eine Abschätzfunktion erweitert. Falls diese gewisse Eigenschaften erfüllt, kann damit der kürzeste Pfad unter Umständen schneller gefunden werden.
Es gibt verschiedene Beschleunigungstechniken für den Dijkstra-Algorithmus, zum Beispiel Arcflag.
Berechnung eines Spannbaumes
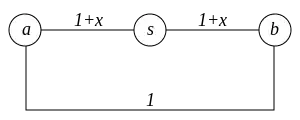
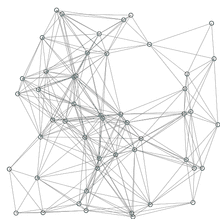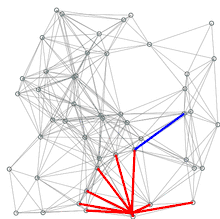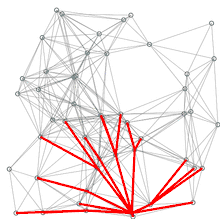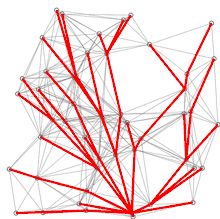
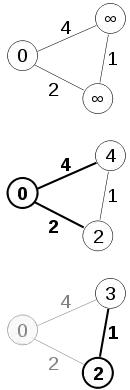
Nach Ende des Algorithmus ist in den Vorgängerzeigern π ein Teil-Spannbaum der Komponente von aus kürzesten Pfaden von zu allen Knoten der Komponente, die in die Queue aufgenommen wurden, verzeichnet. Dieser Baum ist jedoch nicht notwendigerweise auch minimal, wie die Abbildung zeigt:
Sei eine Zahl größer 0. Minimal spannende Bäume sind entweder durch die Kanten und oder und gegeben. Die Gesamtkosten eines minimal spannenden Baumes betragen . Dijkstras Algorithmus liefert mit Startpunkt die Kanten und als Ergebnis. Die Gesamtkosten dieses spannenden Baumes betragen .
Die Berechnung eines minimalen Spannbaumes ist mit dem Algorithmus von Prim oder dem Algorithmus von Kruskal möglich.
Zeitkomplexität
Die folgende Abschätzung gilt nur für Graphen, die keine negativen Kantengewichte enthalten.
Die Laufzeit des Dijkstra-Algorithmus hängt ab von der Anzahl der Kanten und der Anzahl der Knoten . Die genaue Zeitkomplexität hängt von der Datenstruktur ab, in der die Knoten gespeichert werden. Für alle Implementierungen von gilt:
wobei und für die Komplexität der decrease-key- und extract-minimum-Operationen bei stehen. Die einfachste Implementierung für ist eine Liste oder ein Array. Dabei ist die Zeitkomplexität .
Im Normalfall wird man hier auf eine Vorrangwarteschlange zurückgreifen, indem man dort die Knoten als Elemente mit ihrer jeweiligen bisherigen Distanz als Schlüssel/Priorität verwendet.
Die optimale Laufzeit für einen Graphen beträgt mittels Verwendung eines Fibonacci-Heap für den Dijkstra-Algorithmus.[5]
Anwendungen
Routenplaner sind ein prominentes Beispiel, bei dem dieser Algorithmus eingesetzt werden kann. Der Graph repräsentiert hier das Verkehrswegenetz, das verschiedene Punkte miteinander verbindet. Gesucht ist die kürzeste Route zwischen zwei Punkten.
Einige topologische Indizes, etwa der J-Index von Balaban, benötigen gewichtete Distanzen zwischen den Atomen eines Moleküls. Die Gewichtung ist in diesen Fällen die Bindungsordnung.
Dijkstras Algorithmus wird auch im Internet als Routing-Algorithmus im OSPF-, IS-IS- und OLSR-Protokoll eingesetzt. Das letztere Optimized Link State Routing-Protokoll ist eine an die Anforderungen eines mobilen drahtlosen LANs angepasste Version des Link State Routing. Es ist wichtig für mobile Ad-hoc-Netze. Eine mögliche Anwendung davon sind die freien Funknetze.
Auch bei der Lösung des Münzproblems, eines zahlentheoretischen Problems, das auf den ersten Blick nichts mit Graphen zu tun hat, kann der Dijkstra-Algorithmus eingesetzt werden.
Andere Verfahren zur Berechnung kürzester Pfade
Hat man genug Informationen über die Kantengewichte im Graphen, um daraus eine Heuristik für die Kosten einzelner Knoten ableiten zu können, ist es möglich, den Algorithmus von Dijkstra zum A*-Algorithmus zu erweitern. Um alle kürzesten Pfade von einem Knoten zu allen anderen Knoten in einem Graphen zu berechnen, kann man auch den Bellman-Ford-Algorithmus verwenden, der mit negativen Kantengewichten umgehen kann. Der Algorithmus von Floyd und Warshall berechnet schließlich die kürzesten Pfade aller Knoten zueinander.
Literatur
- Thomas H Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein: Algorithmen – eine Einführung. Oldenbourg, München, Wien 2004, ISBN 3-486-27515-1, S. 598–604 (Originaltitel: Introduction to algorithms. Übersetzt von Karen Lippert, Micaela Krieger-Hauwede).
- Robert Sedgewick: Algorithms in C++ Part 5: Graph Algorithms. Indianapolis 2002, ISBN 0-201-36118-3, S. 293–302.
- Edsger W. Dijkstra: A note on two problems in connexion with graphs. In: Numerische Mathematik. 1, 1959, S. 269–271; ma.tum.de (PDF; 739 kB).
Weblinks
- Python-Implementierung mit Erklärungen
- Implementierung in der freien Python-Bibliothek NetworkX
- Interaktives Applet zur Lernen, Ausprobieren und Demonstrieren des Algorithmus
- Java-Applet zu Dijkstra (englisch)
- Interaktive Visualisierung und Animation von Dijkstras Algorithmus, geeignet für Personen ohne Vorkenntnisse von Algorithmen (englisch)
- Implementierung in C (englisch)
- Erklärung anhand eines analogen Modells (PDF; 213 kB)
- Öffentliche Softwarebibliothek in Java mit diesem und anderen Algorithmen (englisch)
- Java Implementierung – Simulation / Auswertung (englisch)
- Dijkstra Algorithmus in C# (csharp). (Memento vom 11. Februar 2013 im Webarchiv archive.today).
Einzelnachweise
- Tobias Häberlein: Praktische Algorithmik mit Python. Oldenbourg, München 2012, ISBN 978-3-486-71390-9, S. 162 ff.
- Rosetta Code: Dijkstra's algorithm
- GeeksforGeeks: Dijkstra’s shortest path algorithm
- The Simple, Elegant Algorithm That Makes Google Maps Possible. Bei: VICE. Abgerufen am 3. Oktober 2020.
- Thomas H. Cormen: Introduction to Algorithms. MIT Press, S. 663.