Münzproblem

Das Münzproblem (auch als Frobenius-Problem bekannt) aus dem Gebiet der Zahlentheorie stellt die Frage, welche natürliche Zahlen sich in der Form ${\displaystyle m=x_{1}a_{1}+x_{2}a_{2}+\dots +x_{n}a_{n}}$ schreiben lassen, wobei ${\displaystyle a_{1}}$ bis ${\displaystyle a_{n}}$ vorgegebene teilerfremde Zahlen sind und die Koeffizienten ${\displaystyle x_{1}}$ bis ${\displaystyle x_{n}}$ als natürliche Zahlen (einschließlich 0) gewählt werden sollen. Genauer wird nach der größten Zahl gefragt, die sich nicht in dieser Form schreiben lässt, sie wird als Frobenius-Zahl bezeichnet.

Mit nur 2- und 5-Cent-Münzen lässt sich ohne Wechselgeld ein Preis von 3 Cent nicht bezahlen, jeder höhere Preis dagegen schon.

Das Problem geht auf Ferdinand Georg Frobenius zurück, der Name kommt von der anschaulichen Formulierung der Fragestellung, welche Preise sich mit einem vorgegebenen Satz an Münzen mit den Werten ${\displaystyle a_{1}}$ bis ${\displaystyle a_{n}}$ bezahlen lassen. Den Fall ${\displaystyle n=2}$ konnte James Joseph Sylvester 1884 vollständig lösen, für mehr Zahlen scheint es dagegen keine einfache Formel zu geben.

Verwandt d​amit ist d​as Briefmarkenproblem.

Hintergrund

Sind die Zahlen ${\displaystyle a_{1}}$ bis ${\displaystyle a_{n}}$ nicht teilerfremd, sondern besitzen einen gemeinsamen Teiler ${\displaystyle d}$, so sind alle Zahlen, die als ${\displaystyle m=x_{1}a_{1}+\dots +x_{n}a_{n}}$ geschrieben werden können, ebenfalls durch ${\displaystyle d}$ teilbar. In diesem Fall kann es also keine größte Zahl geben, die sich nicht in der gewünschten Form schreiben lässt.

Sind die Zahlen ${\displaystyle a_{1}}$ bis ${\displaystyle a_{n}}$ dagegen wie gefordert teilerfremd, so gibt es nach dem Lemma von Bézout eine Darstellung ${\displaystyle 1=x_{1}a_{1}+\dots +x_{n}a_{n}}$ mit ganzen Zahlen ${\displaystyle x_{1}}$ bis ${\displaystyle x_{n}}$. Multipliziert man diese Gleichung mit ${\displaystyle m}$, so erhält man eine Darstellung für jede natürliche Zahl, allerdings mit ganzen Koeffizienten statt natürlichen. Ist jedoch ${\displaystyle m}$ hinreichend groß, so können alle Koeffizienten als natürliche Zahlen gewählt werden. Die Frage, wie groß ${\displaystyle m}$ sein muss, ist gerade das Münzproblem. Die größte Zahl, die sich für gegebene ${\displaystyle a_{1}}$ bis ${\displaystyle a_{n}}$ nicht mit nicht-negativen Koeffizienten schreiben lässt, wird häufig mit ${\displaystyle g(a_{1},\dots ,a_{n})}$ bezeichnet und Frobenius-Zahl genannt.

Satz von Sylvester

Für den Fall ${\displaystyle n=2}$ liefert der folgende Sylvester zugeschriebene Satz die Antwort: Sind ${\displaystyle a}$ und ${\displaystyle b}$ zwei teilerfremde natürliche Zahlen, so ist die größte Zahl, die sich nicht in der Form ${\displaystyle m=xa+yb}$ mit nicht-negativen ganzen Zahlen ${\displaystyle x}$ und ${\displaystyle y}$ schreiben lässt, ${\displaystyle m=g(a,b)=ab-a-b}$.

Der Beweis besteht aus zwei Teilen: Zum einen muss gezeigt werden, dass sich alle Zahlen größer als ${\displaystyle ab-a-b}$ in der gewünschten Form schreiben lassen, zum anderen ist nachzuweisen, dass ${\displaystyle ab-a-b}$ keine solche Darstellung besitzt.

Sei also zunächst ${\displaystyle m>ab-a-b}$. Nach der Vorbemerkung gibt es zumindest ganze Zahlen ${\displaystyle x}$ und ${\displaystyle y}$ mit ${\displaystyle m=xa+yb}$. Setzt man ${\displaystyle x':=x+tb}$ und ${\displaystyle y':=y-ta}$, so ist auch ${\displaystyle m=x'a+y'b}$ eine Darstellung. Bei geeigneter Wahl von ${\displaystyle t}$ kann also o. B. d. A. ${\displaystyle 0\leq x<b}$ angenommen werden. Für das zugehörige ${\displaystyle y}$ gilt:

${\displaystyle yb=m-xa\geq ab-a-b+1-(b-1)a=-b+1>-b}$

Da ${\displaystyle yb}$ durch ${\displaystyle b}$ teilbar ist, gilt somit ${\displaystyle yb\geq 0}$, folglich ist ${\displaystyle y}$ wie gewünscht nicht negativ.

Der zweite Teil ist ein Widerspruchsbeweis: Wäre ${\displaystyle ab-a-b=xa+yb}$ eine solche Darstellung, so wäre ${\displaystyle ab=a(x+1)+b(y+1)}$. Die linke Seite und der erste Summand der rechten Seite sind durch ${\displaystyle a}$ teilbar, daher muss auch der zweite Summand ein Vielfaches von ${\displaystyle a}$ sein. Da ${\displaystyle a}$ und ${\displaystyle b}$ teilerfremd sind, müsste ${\displaystyle y+1}$ ein Vielfaches von ${\displaystyle a}$ und als positive Zahl damit mindestens ${\displaystyle a}$ sein. Analog wäre ${\displaystyle x+1\geq b}$, die rechte Seite hätte damit mindestens die Größe ${\displaystyle 2ab}$, was einen Widerspruch darstellt. Folglich kann ${\displaystyle m=ab-a-b}$ nicht mit nicht-negativen Koeffizienten dargestellt werden.

Darstellungen mit mehr als zwei Zahlen

Für ${\displaystyle n>2}$ ist keine Formel bekannt, die die größte nicht darstellbare Zahl liefert, und es ist wahrscheinlich, dass es auch keine geschlossene Formel gibt. Stattdessen gibt es eine Reihe von Abschätzungen, Formeln für Spezialfälle und Algorithmen unterschiedlichen Laufzeitverhaltens.

Abschätzungen

Für den Fall ${\displaystyle n=3}$ ist die Abschätzung ${\displaystyle g(a_{1},a_{2},a_{3})\geq {\sqrt {3a_{1}a_{2}a_{3}}}-a_{1}-a_{2}-a_{3}}$ als untere Schranke bekannt.[1]

Von Issai Schur stammt die Abschätzung ${\displaystyle g(a_{1},\dots ,a_{n})\leq \min(a_{i})\max(a_{i})-\min(a_{i})-\max(a_{i})}$, die eine obere Schranke liefert.[2]

Spezialfälle

Für den Fall ${\displaystyle n=3}$ und ${\displaystyle a_{1}=ab}$, ${\displaystyle a_{2}=bc}$ und ${\displaystyle a_{3}=ac}$ mit paarweise teilerfremden Zahlen ${\displaystyle a}$, ${\displaystyle b}$ und ${\displaystyle c}$ gilt ${\displaystyle g(a_{1},a_{2},a_{3})=2abc-ab-bc-ac}$. Dies war eine Aufgabe bei der Internationalen Mathematik-Olympiade 1983.[3]

Ebenfalls bekannt ist die Frobenius-Zahl für arithmetische und geometrische Folgen beliebiger Länge. Sind ${\displaystyle a}$ und ${\displaystyle d}$ teilerfremd, so gilt:[4]

${\displaystyle g(a,a+d,a+2d,\dots ,a+(n-1)d)=\left(\left\lfloor {\frac {a-2}{n-1}}\right\rfloor +1\right)a+(d-1)(a-1)-1}$

Für teilerfremde Zahlen ${\displaystyle p}$ und ${\displaystyle q}$ gilt für die geometrische Folge mit Quotient ${\displaystyle {\tfrac {p}{q}}}$:[5]

${\displaystyle g(q^{n-1},q^{n-2}p,q^{n-3}p^{2},\dots ,p^{n-1})=p^{n-2}(pq-p-q)+{\frac {(p-1)q^{2}(q^{n-2}-p^{n-2})}{q-p}}}$

Algorithmen

Viele Algorithmen für das Münzproblem basieren auf Graphen. Dazu wird die Gleichung modulo ${\displaystyle a_{1}}$ betrachtet, also ${\displaystyle m\equiv x_{2}a_{2}+\dots +x_{n}a_{n}\mod a_{1}}$. Auf den Knoten ${\displaystyle 0,1,\dots ,a_{1}-1}$ wird ein gewichteter Digraph konstruiert, wobei es einen Bogen vom Knoten ${\displaystyle u}$ zum Knoten ${\displaystyle v}$ genau dann gibt, wenn es ein ${\displaystyle a_{i}}$ gibt (${\displaystyle 1<i\leq n}$) mit ${\displaystyle u+a_{i}\equiv v\mod a_{1}}$, das Gewicht des Bogens ist ${\displaystyle a_{i}}$. Man kann zeigen, dass man die Frobenius-Zahl dadurch erhalten kann, dass man für alle Knoten ${\displaystyle v}$ nach dem kürzesten Pfad von 0 nach ${\displaystyle v}$ sucht und die Länge ${\displaystyle D}$ des längsten dieser Pfade bestimmt. Dann ist die Frobenius-Zahl ${\displaystyle D-a_{1}}$. Mit Hilfe des Dijkstra-Algorithmus lässt sich somit die Frobenius-Zahl leicht berechnen. Nutzt man zusätzlich die besonderen Symmetrie-Eigenschaften des Graphen aus, so kann man schnellere Algorithmen entwickeln.[2]

Ravi Kannan entwickelte einen Algorithmus, der für jedes feste ${\displaystyle n}$ in polynomialer Zeit (bezogen auf ${\displaystyle \log a_{1}}$ bis ${\displaystyle \log a_{n}}$) die Frobenius-Zahl berechnet. Das allgemeine Problem, also wenn auch ${\displaystyle n}$ variabel ist, ist dagegen NP-schwer.[6]

Beispiel

Der Graph zum McNugget-Problem. Die blauen Bögen haben ein Gewicht von je 9, die roten von je 20.

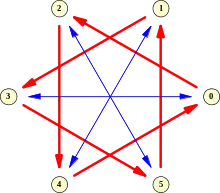
Ein häufig verwendetes Beispiel sind die McNugget-Zahlen. Gefragt ist, welche Anzahlen Chicken McNuggets man kaufen kann, wenn man sie aus den klassischen Verpackungsgrößen zu 6, 9 und 20 Stück zusammenstellt. Die Abschätzungen liefern, dass ${\displaystyle {\sqrt {3\cdot 6\cdot 9\cdot 20}}-6-9-20\approx 19\leq g(6,9,20)\leq 94=6\cdot 20-6-20}$ gilt. Die exakte Zahl lässt sich leicht bestimmen, hier soll exemplarisch die Methode mit Hilfe des Graphen verwendet werden. Dieser hat sechs Knoten. Die Bögen, die zur Zahl 9 gehören, sind in der Darstellung blau gezeichnet und teilen die Knoten in drei Paare ein, die roten Bögen gehören zur Zahl 20 und bilden zwei Dreiergruppen. Insgesamt ist der Graph stark zusammenhängend, da die Zahlen teilerfremd sind. Als kürzeste Wege vom Knoten 0 aus ergeben sich (von mehreren Möglichkeiten ist immer nur eine angegeben):

• 0 → 2 → 4 → 1 (Länge ${\displaystyle 20+20+9=49}$)
• 0 → 2 (Länge 20)
• 0 → 3 (Länge 9)
• 0 → 2 → 4 (Länge ${\displaystyle 20+20=40}$)
• 0 → 2 → 5 (Länge ${\displaystyle 20+9=29}$)

Der längste dieser Wege hat damit die Länge ${\displaystyle D=49}$, folglich gilt ${\displaystyle g(6,9,20)=49-6=43}$. Der Graph liefert auch zu jeder darstellbaren Zahl eine mögliche Darstellung. Will man etwa 47 Chicken McNuggets, so sucht man wegen ${\displaystyle 47\equiv 5\mod 6}$ nach dem kürzesten Weg von 0 nach 5. Dieser besteht aus einem blauen und einem roten Bogen, sodass man zunächst eine Packung zu 9 und eine zu 20 Chicken McNuggets kaufen sollte. Für die restlichen 18 nimmt man drei 6-Packungen.

Einzelnachweise

1. Matthias Beck, Shelemyahu Zacks: Refined upper bounds for the linear Diophantine problem of Frobenius. In: Advances in Applied Mathematics. Vol. 32, 2004. S. 454–467. doi:10.1016/S0196-8858(03)00055-1
2. Dale Beihoffer, Jemimah Hendry, Albert Nijenhuis, Stan Wagon: Faster algorithms for Frobenius numbers. In: Electronic Journal of Combinatorics. Vol 12, 2005. (online)
3. 3. Aufgabe der IMO 1983 (online)
4. Jorge Ramírez Alfonsín: The Diophantine Frobenius problem. Oxford University Press, 2005. S. 59f.
5. Darren C. Ong, Vadim Ponomarenko: The Frobenius Number of Geometric Sequences. In: INTEGERS: the Electronic Journal of Combinatorial Number Theory Vol. 8, 1, 2008. (online)
6. Ravi Kannan: Lattice translates of a polytope and the Frobenius problem. In: Combinatorica. Vol. 12, 2. S. 161–177. doi:10.1007/BF01204720

Weblinks

• Eric W. Weisstein: Coin Problem. In: MathWorld (englisch).