Spektrales Clustering
Das spektrale Clustering ist ein Verfahren der Clusteranalyse. Die zu clusternden Objekte werden als Knoten eines Graphen betrachtet. Die Distanzen oder Unähnlichkeiten zwischen den Objekten werden durch die gewichteten Kanten zwischen den Knoten des Graphen repräsentiert. Graphentheoretische Resultate über Laplace-Matrizen von Graphen mit Zusammenhangskomponenten sind die Grundlage des spektralen Clusterings. Die Eigenwerte einer Matrix werden auch Spektrum genannt, daher stammt der Name des Verfahrens. Die graphentheoretischen Grundlagen wurden von Donath & Hoffman (1973) sowie Fiedler (1973) gelegt.[1][2]
Mathematische Grundlagen
Graphenreduktion
In einem ersten Schritt wird der Graph reduziert. Ziel ist es dabei, alle Kanten mit zu großen Gewichten aus dem Graphen zu entfernen. Folgende Ansätze gibt es:
- Nachbarschaftsgraph
- Wenn das Kantengewicht größer als ist, dann wird diese Kante aus dem Graph entfernt.
- k-nn Graphen ( nächste Nachbarngraphen)
- Alle Kanten zu einem Knoten werden nach dem Kantengewicht sortiert. Hat eine Kante ein größeres Kantengewicht als das kleinste Kantengewicht, dann wird diese Kante aus dem Graph entfernt. Die -nn Relation ist jedoch nicht symmetrisch, d. h. es kann passieren, dass das Kantengewicht kleiner ist als das kleinste Kantengewicht zum Objekt , aber nicht kleiner ist als das kleinste Kantengewicht zum Objekt . Man spricht von einem k-nn Graph, wenn die Kante im Graph bleibt, falls für mindestens eines der Objekte oder gilt, dass kleiner ist als das kleinste Kantengewicht zum Objekt, d. h. jedes Objekt hat mindestens Kanten. Im Gegensatz dazu enthält ein gemeinsamer k-nn Graph nur die Kante, wenn für beide Objekte gilt, dass kleiner ist als das kleinste Kantengewicht der Objekten, d. h. jedes Objekt hat maximal Kanten.
- Voll verbundener Graph
- Mit Hilfe einer Ähnlichkeitsfunktion werden die Kantengewichte aus den Distanzen zwischen den Objekten berechnet. Ein Beispiel für eine Ähnlichkeitsfunktion ist die gaußsche Ähnlichkeitsfunktion . Der Parameter kontrolliert die Größe der Nachbarschaft wie auch die Parameter oder .
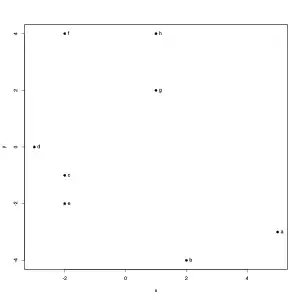 Position von 8 Objekten in einem zweidimensionalen Raum.
Position von 8 Objekten in einem zweidimensionalen Raum. Voll verbundener Graph mit den euklidischen Distanzen an den Kanten für die 8 Objekte.
Voll verbundener Graph mit den euklidischen Distanzen an den Kanten für die 8 Objekte.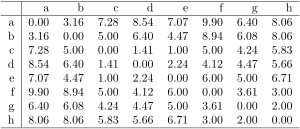 Distanzmatrix der euklidischen Distanzen für die 8 Objekte.
Distanzmatrix der euklidischen Distanzen für die 8 Objekte.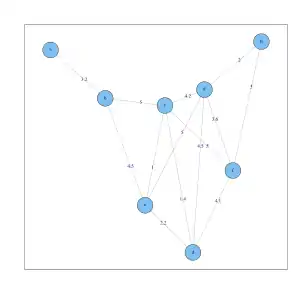 Nachbarschaftsgraph ( ) für die 8 Objekte.
Nachbarschaftsgraph ( ) für die 8 Objekte.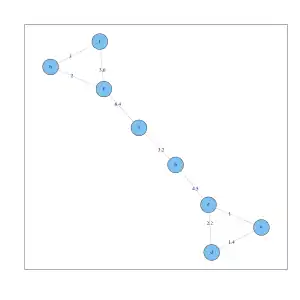 k-nn Graph () für die 8 Objekte. Jeder Knoten hat mindestens zwei Kanten.
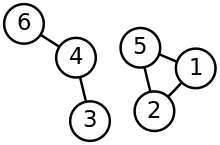
k-nn Graph () für die 8 Objekte. Jeder Knoten hat mindestens zwei Kanten.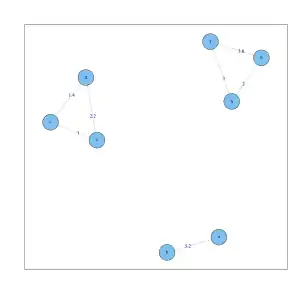 Gemeinsamer k-nn Graph () für die 8 Objekte. Jeder Knoten hat maximal zwei Kanten. Der Datensatz zerfällt in 3 Zusammenhangskomponenten.
Gemeinsamer k-nn Graph () für die 8 Objekte. Jeder Knoten hat maximal zwei Kanten. Der Datensatz zerfällt in 3 Zusammenhangskomponenten.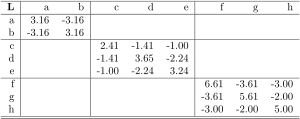 Laplace-Matrix des gemeinsamen k-nn Graphen () für die 8 Objekte.
Laplace-Matrix des gemeinsamen k-nn Graphen () für die 8 Objekte.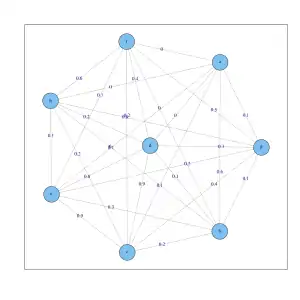 Voll verbundener Graph mit den Werten der gaußschen Ähnlichkeitsfunktion () an den Kanten für die 8 Objekte.
Voll verbundener Graph mit den Werten der gaußschen Ähnlichkeitsfunktion () an den Kanten für die 8 Objekte.
Laplace-Matrizen
Aus den Kantengewichten wird für die Objekte die (gewichtete) Adjazenzmatrix gebildet. Die Diagonalmatrix enthält auf der Diagonalen die Summe der Kantengewichte, die zu einem Knoten führen (nach der Graphenreduktion). Dann können drei Laplace-Matrizen berechnet werden:
- nicht-normalisierte Matrix ,
- die normalisierte Matrix und
- die normalisierte Matrix .
Für alle Vektoren gilt
Da die Laplace-Matrizen symmetrisch und positiv-semidefinit sind, sind alle Eigenwerte reellwertig und größer gleich Null. Für die Laplace-Matrix kann man zeigen, dass mindestens ein Eigenwert gleich Null ist. Besteht der Graph aus Zusammenhangskomponenten, dann sind die Laplace-Matrizen Blockmatrizen (siehe Grafik und Matrix oben). Dabei hat jeder Block einen Eigenwert gleich Null. Für die Eigenvektoren zum Eigenwert Null muss sein. Da alle Kantengewichte positiv sind, müssen alle Einträge der Knoten einer Zusammenhangskomponente gleich sein (damit gilt). Analog gilt dies für , nur dass die Einträge im Eigenvektor mit gewichtet sind, während für die Einträge im Eigenvektor gleich Eins sind.
Zum Clustern analysiert man die kleinsten Eigenwerte und -vektoren der Laplace-Matrizen.
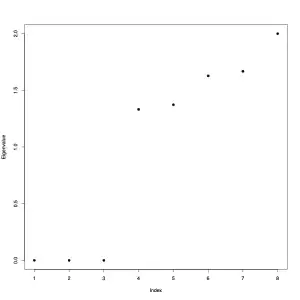 Eigenwerte der Laplace-Matrix des Gemeinsamen k-nn Graph () für die 8 Objekte Daten. Da der Graph aus drei Zusammenhangskomponenten besteht ergeben sich drei Eigenwerte mit dem Wert Null.
Eigenwerte der Laplace-Matrix des Gemeinsamen k-nn Graph () für die 8 Objekte Daten. Da der Graph aus drei Zusammenhangskomponenten besteht ergeben sich drei Eigenwerte mit dem Wert Null.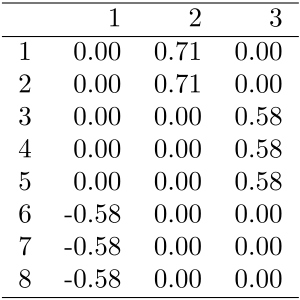 Werte der drei Eigenvektoren zum Eigenwert Null der Laplace-Matrix . Die Einträge sollten gleich Eins sein, aber die Software reskaliert die Eigenvektoren, so dass sie die Länge Eins haben.
Werte der drei Eigenvektoren zum Eigenwert Null der Laplace-Matrix . Die Einträge sollten gleich Eins sein, aber die Software reskaliert die Eigenvektoren, so dass sie die Länge Eins haben.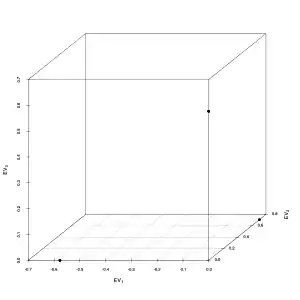 3D-Streudiagramm der drei Eigenvektoren zu den Null-Eigenwerten. Die acht Objekte werden an drei Positionen geplottet (overplotting), so dass ein k-Means Clustering die drei Zusammenhangskomponenten perfekt finden kann.
3D-Streudiagramm der drei Eigenvektoren zu den Null-Eigenwerten. Die acht Objekte werden an drei Positionen geplottet (overplotting), so dass ein k-Means Clustering die drei Zusammenhangskomponenten perfekt finden kann.
Algorithmen
Verschiedene Spektrale-Clustering-Algorithmen wurden entwickelt:
- Nicht-normalisiertes spektrales Clustering
- Berechne die nicht-normalisierte Laplace-Matrix
- Berechne die ersten Eigenvektoren (das sind die Eigenvektoren mit den kleinsten Eigenwerten)
- Nimm die Zeilen der Eigenvektoren und clustere sie mit einem partitionierenden Verfahren, z. B. dem k-Means-Algorithmus
- Normalisiertes spektrales Clustering nach Shi und Malik[4]
- Berechne die normalisierte Laplace-Matrix
- Berechne die ersten Eigenvektoren (das sind die Eigenvektoren mit den kleinsten Eigenwerten)
- Nimm die Zeilen der Eigenvektoren und clustere sie mit einem partitionierenden Verfahren
- Normalisiertes spektrales Clustering nach Ng, Jordan und Weiss[5]
- Berechne die normalisierte Laplace-Matrix
- Berechne die ersten Eigenvektoren (das sind die Eigenvektoren mit den kleinsten Eigenwerten)
- Nimm die Zeilen der Eigenvektoren und clustere sie mit einem partitionierenden Verfahren
Bezüglich der Wahl der Verfahrensparameter bzw. -algorithmen empfiehlt das Tutorial von Ulrike von Luxburg:[6]
- Wahl des Nachbarschaftsgraph: der k-nn Graph, da er verschieden dichte Cluster besser erkennen kann und eine dünn besetzte Laplace-Matrix erzeugt. Außerdem kann in einem größeren Bereich variieren, ohne dass sich die Clusteranalyse stark verändert.
- Wahl der Parameter des Nachbarschaftsgraphs:
- Für den k-nn Graph sollte so gewählt werden, dass der Graph nicht weniger Zusammenhangskomponenten hat als man Cluster erwartet.
- Für den gemeinsamen k-nn Graph sollte größer sein als beim k-nn Graph, da der gemeinsame k-nn Graph weniger Kanten enthält als der k-nn Graph. Eine Heuristik für die Wahl von ist nicht bekannt.
- Für den Nachbarschaftsgraph sollte man gleich der längsten Kante im minimalen Spannbaum (engl. minimal spanning tree) wählen.
- Für den voll verbundenen Graph mit der gaußsche Ähnlichkeitsfunktion sollte so gewählt werden, dass der resultierende Graph dem k-nn Graph oder dem Nachbarschaftsgraph entspricht. Daumenregel sind auch: gleich der längsten Kante im minimalen Spannbaum oder als die mittlere Distanz zum nächsten Nachbarn mit .
- Wahl der Clusteranzahl: Man plottet die Eigenwerte der Laplace-Matrix, sortiert nach der Größe und sucht nach Sprüngen, z. B. in der Grafik oben zwischen dem 3. und 4. Eigenwert bei dem 8-Objekte Datensatz.
- Wahl der Laplace-Matrix: Da die Einträge im Eigenvektor gleich Eins sind bei , kann z. B. der k-Means-Algorithmus gut clustern.
Beispiel
Der Iris Datensatz wurde von Sir Ronald Fisher (1936) als Beispiel für eine Diskriminanzanalyse benutzt.[7] Manchmal wird er auch ‚Anderson's Iris Datensatz‘ genannt, weil Edgar Anderson die Daten erhoben hat um die morphologische Variation in Schwertlilien zu quantifizieren.[8] Der Datensatz besteht aus jeweils 50 Exemplaren von drei Arten: der Borsten-Schwertlilie (Iris setosa), der Schillernde Schwertlilie (Iris versicolor) und der Virginische Schwertlilie (Iris virginica). An einem Kelchblatt (engl. sepal) und an einem Kronblatt (engl. petal) wurden jeweils die Länge und Breite gemessen. Der Datensatz enthält also 150 Beobachtungen und 4 Variablen.
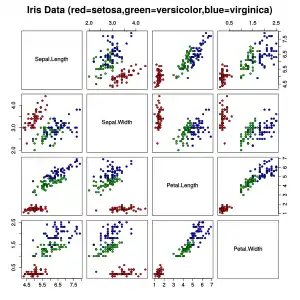 Streudiagrammmatrix des Iris Datensatzes. Die Farben der Datenpunkte entsprechen den drei Arten.
Streudiagrammmatrix des Iris Datensatzes. Die Farben der Datenpunkte entsprechen den drei Arten.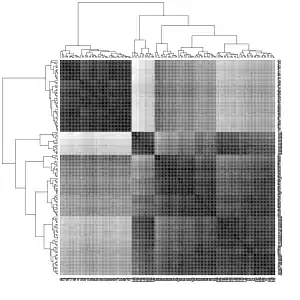 Heatmap der euklidischen Distanzen im Iris Datensatz. Je dunkler die Farbe desto kleiner ist die Distanz zwischen den Objekten.
Heatmap der euklidischen Distanzen im Iris Datensatz. Je dunkler die Farbe desto kleiner ist die Distanz zwischen den Objekten.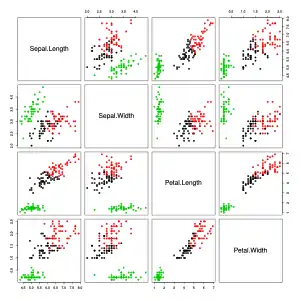 Ergebnis des spektralen Clusterings auf dem Iris Datensatz.
Ergebnis des spektralen Clusterings auf dem Iris Datensatz.
Wie man in der linken (ersten) Grafik in der Streudiagrammmatrix sieht, unterscheidet sich eine der drei Arten (rot in der Grafik) deutlich von den anderen Arten. Die beiden anderen Arten können nur schwer voneinander getrennt werden. Die mittlere (zweite) Grafik zeigt die euklidischen Distanzen zwischen den Objekten in einer Heatmap mit Graustufen. Je dunkler das Grau ist, desto näher sind sich die Objekte. Dabei sind die Objekte bereits so umgeordnet worden, dass Objekte mit ähnlichen Distanzen zu anderen Objekten nahe beieinander sind. Die verwendete Software nutzt ein hierarchisches Clusterverfahren dazu und zeigt auch die Dendrogramme. Die rechte (dritte) Grafik zeigt das Ergebnis des spektralen Clusterings. Man sieht, dass die gefundenen Cluster einigermaßen mit den drei Arten übereinstimmen.
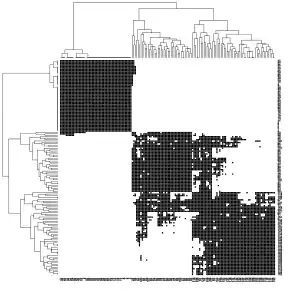 Schwarz: Kanten zwischen Objekten, die bei einem k-nn Graph () erhalten bleiben. Weiß: Kanten, die gelöscht wurden.
Schwarz: Kanten zwischen Objekten, die bei einem k-nn Graph () erhalten bleiben. Weiß: Kanten, die gelöscht wurden.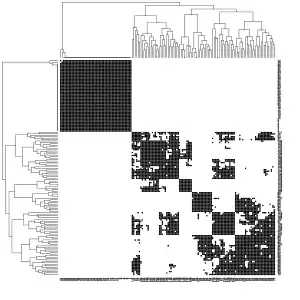 Schwarz: Kanten zwischen Objekten, die bei einem gemeinsamen k-nn Graph () erhalten bleiben. Weiß: Kanten, die gelöscht wurden.
Schwarz: Kanten zwischen Objekten, die bei einem gemeinsamen k-nn Graph () erhalten bleiben. Weiß: Kanten, die gelöscht wurden.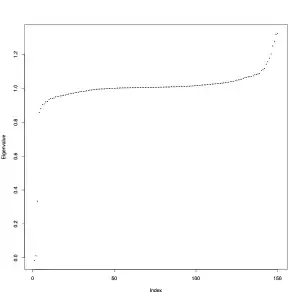 Streudiagramm der Eigenwerte der Laplace-Matrix für den k-nn Graph ().
Streudiagramm der Eigenwerte der Laplace-Matrix für den k-nn Graph ().
Die beiden linken Bilder zeigen, welche Kanten im k-nn Graph bzw. gemeinsamen k-nn Graph beibehalten wurden (schwarz) oder nicht (weiß). Für den Parameter wurde dabei zunächst die längste Kante in einem minimalen Spannbaum bestimmt und dann für alle Beobachtungen berechnet, welcher Nachbarschaftsanzahl es entspricht. Als mittlere Wert ergab sich ca. 60 Nachbarn und es wurde dann gewählt. Danach wurde die Laplace-Matrix berechnet sowie deren Eigenwerte. Das Diagramm der Eigenwerte zeigt große Sprünge nach dem zweiten bzw. dem dritten Eigenwert an. Die ersten drei Eigenvektoren wurden dann einem k-Means-Clustering mit 3 Clustern unterzogen.
| Cluster | |||
|---|---|---|---|
| Art | 1 | 2 | 3 |
| setosa | 0 | 0 | 50 |
| versicolor | 43 | 7 | 0 |
| virginica | 7 | 43 | 0 |
Die Konfusionsmatrix zeigt, dass das Spektral Clustering einigermaßen die Arten wiederentdeckt hat. Der Setosa-Cluster ist komplett richtig gefunden worden. Bei den Versicolor- und Virginica-Clustern sind jeweils sieben Beobachtungen falsch klassifiziert worden, das entspricht einer Falsch-Klassifikationsrate von .
Einzelnachweise
- W. E. Donath, A. J. Hoffman: Lower bounds for the partitioning of graphs. In: IBM Journal of Research and Development. 17(5), (1973), S. 420–425.
- M. Fiedler: Algebraic connectivity of graphs. In: Czechoslovak Mathematical Journal. 23(2), (1973), S. 298–305.
- Ulrike von Luxburg: A Tutorial on Spectral Clustering. 2007, abgerufen am 6. Januar 2018.
- J. Shi, J. Malik: Normalized cuts and image segmentation. In: IEEE Transactions on Pattern Analysis and Machine Intelligence. 22(8), (2000), S. 888–905. doi:10.1109/34.868688
- A. Y. Ng, M. I. Jordan, Y. Weiss: On spectral clustering: Analysis and an algorithm. In: Advances in Neural Information Processing Systems. 2, 2002, S. 849–856.
- Ulrike von Luxburg: A tutorial on spectral clustering. (PDF; 411 kB). In: Statistics and Computing. 17(4), (2007), S. 395–416. doi:10.1007/s11222-007-9033-z
- R. A. Fisher: The use of multiple measurements in taxonomic problems. In: Annals of Eugenics. 7(2), (1936), S. 179–188. doi:10.1111/j.1469-1809.1936.tb02137.x
- E. Anderson: The species problem in Iris. In: Annals of the Missouri Botanical Garden. 1936, S. 457–509.