Cluster (Datenanalyse)

Als Cluster (gelegentlich auch Ballungen) bezeichnet man in der Informatik und Statistik eine Gruppe von Datenobjekten mit ähnlichen Eigenschaften. Die Menge der in einem Datensatz gefundenen Cluster bezeichnet man als Clustering, Verfahren zur Berechnung einer solchen Gruppierung als Clusteranalyse. Nicht zu einem Cluster gehörende Datenobjekte bezeichnet man als Ausreißer (englisch outlier) oder Rauschen (englisch noise).

Die Kernidee eines Clusters ist, dass Objekte im gleichen Cluster über „ähnliche“ Eigenschaften verfügen und sich von Objekten, die nicht im selben Cluster sind, dadurch unterscheiden.

Clusterzugehörigkeit

Bereits bei der Clusterzugehörigkeit gibt es unterschiedliche Formulierungen.

Bei einem harten Clustering gehört jedes Datenobjekt ganz oder gar nicht zu einem Cluster.
Bei einem weichen Clustering gehört jedes Datenobjekt zu einem gewissen Anteil zu einem Cluster.

Des Weiteren kann man unterscheiden:

Bei einem strikt partitionierenden Clustering gehört jedes Datenobjekt zu genau einem Cluster.
Bei einem strikt partitionierenden Clustering mit Ausreißern kann ein Datenobjekt auch zu keinem Cluster gehören (bei einem weichen Clustering dürfen sich die Anteile auch zu weniger als 1 summieren).
Bei einem überlappenden Clustering kann ein Objekt auch zu mehreren Clustern gehören (bei einem weichen Clustering dürfen sich die Anteile auch zu mehr als 1 summieren).

Auch innerhalb von Clustern kann es Untergruppen geben, die einander ähnlicher sind als dem Rest der größeren Gruppe. Hat man eine derartige Struktur, so spricht man von hierarchischen Clustern bzw. einem hierarchischen Clustering. Verfahren, die hierarchische Cluster finden können, sind beispielsweise Hierarchische Clusteranalyse, OPTICS und BIRCH.

Modelle von Clustern

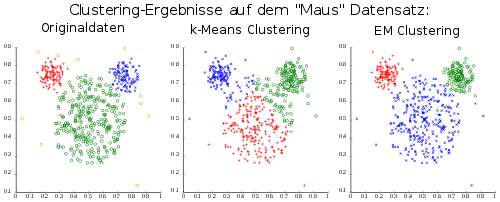
Vergleich k-Means und EM-Algorithmus auf einem künstlichen Datensatz, visualisiert mit ELKI. Durch Verwendung von Varianzen kann EM die unterschiedlichen Normalverteilungen akkurat beschreiben, während k-Means die Daten in ungünstige Voronoi-Zellen aufteilt.

Verschiedene Algorithmen zur Clusteranalyse verwenden oft unterschiedliche Begriffe von Clustern. Dies führt oftmals zu Verständnisproblemen, da die Ergebnisse eines Verfahrens nicht im Sinne eines anderen Verfahrens ähnlich sein müssen.

So beschreibt der k-Means-Algorithmus Cluster durch ihre Mittelpunkte (bzw. die daraus entstehenden Voronoi-Zellen), der EM-Algorithmus Cluster durch Mittelpunkt und eine Kovarianzmatrix, während DBSCAN "dichte-verbundene" Mengen beliebiger Form als Cluster berechnet.

Je nach verwendetem Clusterbegriff können unterschiedliche Strukturen gefunden oder auch nicht gefunden werden. In dem hier gezeigten Beispiel können die vorhandenen Cluster vom k-Means-Algorithmus durch dessen Cluster-Modell nicht akkurat gefunden werden. Das komplexere Modell des EM-Algorithmus hingegen eignet sich optimal, um diese Daten zu beschreiben, da sie von einer Normalverteilung erzeugt wurden.

Subspace-Cluster

Als Subspace-Cluster bezeichnet man einen Cluster, der nicht in allen Attributen oder Attributkombinationen auffällig ist. Erst wenn die Daten geeignet projiziert werden, erkennt man die höhere Ähnlichkeit der Clusterobjekte im Vergleich zu den anderen.

Bei Subspace-Clustern kann man unterscheiden zwischen Achsenparallelen Clustern (basierend auf einer Attributauswahl) und beliebig orientierten Correlation-Clustern.

Verfahren für Subspace-Clusterverfahren sind beispielsweise CLIQUE, ORCLUS, SubClu, PreDeCon, PROCLUS, HiSC, HiCO, 4C, ERiC und CASH.

Berechnung von Clustern

Es gibt zahlreiche Verfahren (sogenannte Clusteranalyse-Algorithmen) zur Berechnung von Clustern. Diese unterscheiden sich wesentlich darin, was für Modelle sie für Cluster verwenden. Bei vielen klassischen Verfahren wie dem k-Means-Algorithmus, dem EM-Algorithmus, der hierarchischen Clusteranalyse und DBSCAN steht das Cluster-Modell im Vordergrund, und es gibt zum Teil mehrere konkrete Algorithmen, eine (zumindest lokal) optimale Lösung für dieses Modell zu finden. Viele neuere Verfahren hingegen haben kein entsprechend klar definiertes Modell mehr.

Bewertung von Clustern

Die Bewertung von gefundenen Clustern ist kein einfaches Problem, insbesondere, wenn die Cluster aus unterschiedlichen Verfahren stammen. Es besteht die Gefahr der Überanpassung, wenn die Bewertungsmethode einem der verwendeten Verfahren zu ähnlich ist – das bedeutet, man untersucht letztlich, welches Verfahren der Bewertungsmethode am ähnlichsten ist.

Interne Bewertung

Von einer internen Bewertung spricht man, wenn zur Bewertung keine zusätzlichen Informationen verwendet werden, sondern lediglich die Objekte des Datensatzes zur Bewertung verwendet werden. Typischerweise verwendet man hierzu Distanzmaße, beispielsweise die durchschnittliche Distanz zweier Clusterobjekte zueinander. Die interne Bewertung bevorzugt normalerweise Clusteringergebnisse, die nach demselben Modell erstellt wurden. So haben beispielsweise von $k$ -Means gefundene Cluster natürlicherweise geringere durchschnittliche Abstände als DBSCAN-Cluster. Daher ist diese Art der Bewertung vor allem sinnvoll, wenn man unterschiedliche Ergebnisse des gleichen Verfahrens bewerten will, beispielsweise von mehreren Läufen eines randomisierten Verfahrens wie dem $k$ -Means-Algorithmus. Ein von der Anzahl der Cluster unabhängiges internes Maß zur Bewertung von distanzbasierten Clusterings stellt der Silhouettenkoeffizient dar. Er eignet sich vor allem dazu, Ergebnisse von $k$ -Means mit unterschiedlichen Werten von $k$ zu vergleichen, da er von der Clusteranzahl $k$ unabhängig ist.

Externe Bewertung

Bei der externen Bewertung wird Information hinzugenommen, die nicht während der Clusteranalyse verwendet wurde. Existiert beispielsweise eine Klasseneinteilung der Daten, so kann die Übereinstimmung des Clusters mit einer Klasse zur Bewertung verwendet werden. Die Probleme bei diesem Ansatz liegen darin, dass zum einen nicht immer eine geeignete Information zur Verfügung steht, zum anderen das Ziel der Clusteranalyse eben genau die Entdeckung von neuer Struktur ist, und die Bewertung anhand einer bekannten Struktur daher nur bedingt sinnvoll ist. Des Weiteren können in den Daten mehrere, sich überlappende Strukturen existieren.[1] Durch die Koppelung an die bestehende Klasseneinteilung bevorzugt diese Bewertung informierte Verfahren aus dem Bereich des Maschinellen Lernen gegenüber uninformierten Verfahren aus der (echten) Clusteranalyse.

Siehe auch

Einzelnachweise

I. Färber, S. Günnemann, H.-P. Kriegel, P. Kröger, E. Müller, E. Schubert, T. Seidl, A. Zimek: On Using Class-Labels in Evaluation of Clusterings. In: MultiClust: 1st International Workshop on Discovering, Summarizing and Using Multiple Clusterings Held in Conjunction with KDD 2010, Washington, DC. 2010 (lmu.de [PDF]).

Literatur

Martin Ester, Jörg Sander: Knowledge Discovery in Databases. Techniken und Anwendungen. Springer, Berlin 2000, ISBN 3-540-67328-8.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] I. Färber, S. Günnemann, H.-P. Kriegel, P. Kröger, E. Müller, E. Schubert, T. Seidl, A. Zimek: On Using Class-Labels in Evaluation of Clusterings. In: MultiClust: 1st International Workshop on Discovering, Summarizing and Using Multiple Clusterings Held in Conjunction with KDD 2010, Washington, DC. 2010 (lmu.de [PDF]).