Hohlspiegel
Ein Hohlspiegel ist ein konkav (nach innen) gewölbter Spiegel (Konkavspiegel). Praktische Verwendung finden vor allem Hohlspiegel in Form eines Kugelausschnitts („sphärische“ Spiegel) und in Form von Rotationsparaboloiden (siehe auch Parabolspiegel).

Ein Hohlspiegel, der zum Konzentrieren von Strahlen in seinem Brennpunkt (Fokus) dient (z. B. Sonnenstrahlen bei der Nutzung von Sonnenenergie in Sonnenkraftwerken), wird Brennspiegel genannt.[1]
Geschichte

Der französische Arzt Pierre Borel, Mitglied der Pariser Académie des sciences, setzte im 17. Jahrhundert den Hohlspiegel als Untersuchungsinstrument ein. Zum Zwecke der medizinischen Untersuchung und besseren Ausleuchtung von Körperöffnungen konstruierte er einen Hohlspiegel zur Reflexion und Fokussierung des Lichtes auf das zu untersuchende Objekt.[2] Leicht modifiziert werden Hohlspiegel heute noch als Stirnspiegel oder -reflektoren in der medizinischen Diagnostik eingesetzt.
Für frühere Beschreibungen des Hohlspiegels siehe auch Archimedes – Brennspiegel, Alhazen (dort insbesondere zum Alhazenschen Problem) und Schatz der Optik (dort besonders die Abbildung des Titelblatts).
Zwei Hauptvarianten
Analog zu sphärischen und asphärischen Sammellinsen gibt es auch bei Hohlspiegeln zwei Bauformen. Dabei hat die aufwendigere und teurere Bauform den Vorteil, die sphärische Aberration weitgehend zu unterdrücken.
Parabolspiegel
Nur beim Parabolspiegel werden alle Lichtstrahlen, die parallel zur optischen Achse einfallen, exakt im Brennpunkt (Fokus) gebündelt. Die Parabolform ist aber in der Herstellung etwas aufwendiger als die sphärische Form.
Sphärischer Hohlspiegel
Einen Parabolspiegel kann man für geringe Krümmungswinkel durch eine Kugelfläche annähern, und zwar mit einer Genauigkeit, die für viele Anwendungen ausreicht. Ein sphärischer Spiegel ist wesentlich einfacher herzustellen als ein Parabolspiegel, sodass er oft den Vorzug erhält.
Die optische Eigenschaft des Hohlspiegels wird bestimmt durch den Radius der Kugel, deren Wandsegment er darstellt, den sogenannten Wölbungsradius. Stellt man in das Zentrum der Kugel eine (gedachte) punktförmige Lichtquelle, so reflektiert der Spiegel das Licht der Quelle wieder auf diese zurück. Kommen die Lichtstrahlen parallel aus dem Unendlichen, so reflektiert der Spiegel sie zum Fokus (Brennpunkt). Dieser liegt in etwa auf halbem Weg zwischen Zentrum und Spiegel. Die Brennweite eines Hohlspiegels beträgt also die Hälfte seines Kreisradius. Allerdings erfolgt die Vereinigung der Lichtstrahlen wegen der sphärischen Aberration dort nur unvollkommen: Die Lichtstrahlen bilden in der Nähe des Fokus eine Katakaustik genannte Figur. (Das wird dagegen beim Parabolspiegel vermieden.)
Optische Abbildung
Die Betrachtungen werden unter der Annahme angestellt, dass sie in einem Winkelbereich stattfinden, wo sphärischer und Parabolspiegel sich etwa gleich verhalten.
Blickt man innerhalb der Brennweite, also zwischen Spiegel und Brennpunkt, in einen Hohlspiegel, sieht man sich selbst vergrößert, wobei das Bild wie in einem Planspiegel aufrecht und seitenverkehrt ist. Blickt man von außerhalb des Brennpunktes in einen Hohlspiegel, steht das reflektierte Bild auf dem Kopf. Das durch einen Hohlspiegel erzeugte Bild ist über das Reflexionsgesetz berechenbar (siehe auch: optische Abbildung).
Hohlspiegel werden unter anderem als Hauptspiegel in Spiegelteleskopen, in optischen Spektrometern und Monochromatoren sowie als Rasierspiegel verwendet. Auch die Satellitenschüsseln für den Fernsehempfang oder Radarantennen funktionieren nach demselben Prinzip, allerdings für die dem Licht verwandten Radiowellen.
Strahlengänge bei verschiedenen Gegenstandsweiten
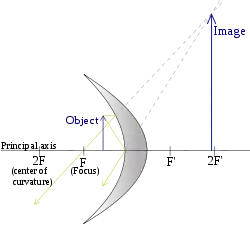
Ähnlich wie bei der Konvexlinse entsteht ein virtuelles Bild, wenn die Gegenstandsweite kleiner als die Brennweite ist (siehe Lupe). Ein typisches Beispiel ist der Kosmetikspiegel, der nur eine geringe Wölbung und damit eine große Brennweite aufweist. Die Brennweite ist also größer als der Abstand des Betrachters (der in diesem Fall der Gegenstand ist) zum Spiegel.
Die Vergrößerung gegenüber einem Planspiegel bei gleichem Betrachtungsabstand ist maximal 2-fach (beide Spiegel im Abstand der Brennweite des Hohlspiegels). Wird der Planspiegel jedoch so nah positioniert, dass das Spiegelbild gerade noch scharf gesehen werden kann, so vergrößert der im Abstand stehende Hohlspiegel um den Faktor . Diese Vergrößerung lässt sich durch Verringerung des Abstandes zum Hohlspiegel noch geringfügig steigern.[3]
Die Form des Spiegels ist variabel, bei Hohlspiegeln ist sie meist rund, wobei auf der Rückseite oft noch ein Normalspiegel eingelassen ist. Der Kosmetikspiegel besitzt in der Regel auch ein Gestell, um ihn aufrecht platzieren oder auch aufhängen zu können.
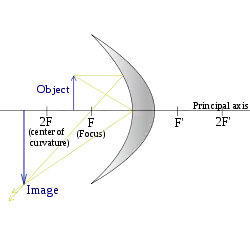
Bei Gegenstandsweiten größer der Brennweite entsteht, ebenfalls ähnlich der Konvexlinse, generell ein invertiertes reelles Bild (Ausnahme: Gegenstandsweite gleich Brennweite; s. u.). Die Vergrößerung hängt dabei vom Verhältnis Gegenstandsweite zur Brennweite ab. Ein Beispiel ist hier der Teleskopspiegel, bei dem die Gegenstandsweite sehr groß ist, und ein stark verkleinertes Bild nahe der Brennebene entsteht (damit ein Stern auf eine Fotoplatte passt, muss er extrem verkleinert werden).
| Gegenstandsweite (G), Brennweite (F) |
Bild | Strahlengang |
|---|---|---|
| (Objekt zwischen Spiegel und Brennpunkt) |
|
 |
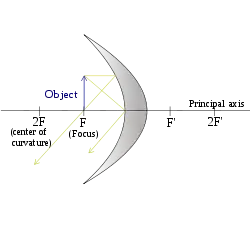
| (Objekt befindet sich in der Brennebene) |
|
 |
(Objekt befindet sich zwischen der einfachen und doppelten Brennweite) |
|
 |
| (die Gegenstandsweite entspricht der doppelten Brennweite) |
|
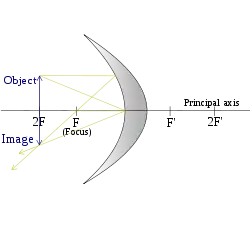 |
(die Gegenstandsweite ist größer als die doppelte Brennweite) |
|
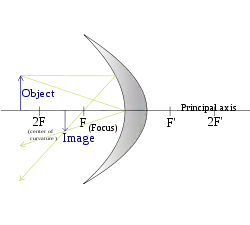 |
Sonstiges
In der Zeitschrift Der Spiegel gibt es auf der vorletzten Seite eine Spalte mit dem Titel Hohlspiegel. Dort werden lustige, kuriose bzw. unfreiwillig komische Zeitungsausschnitte, Zeitungsüberschriften, Annoncen, Ausschnitte aus Gebrauchsanleitungen u. ä. zitiert.[4][5]
Weblinks
Einzelnachweise
- Brennspiegel. In: Lexikon der Physik. Spektrum Akademischer Verlag, Heidelberg 1998 (online).
- Nezhat's History of Endoscopy, Chapter 3 HTML-Version, PDF-Version (Memento des Originals vom 7. Oktober 2013 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.
- J. Hattenbach: Die Vergrößerung des eigenen Spiegelbilds im Kosmetikspiegel
- Hohlspiegel – Die besten Fundstücke. Heyne-Verlag, München 2010, ISBN 978-3-453-60164-2.
- Best of Hohlspiegel 2008. bei Spiegel-Online