Auflösung (Mikroskopie)

Unter optischer oder räumlicher Auflösung versteht man in der Mikroskopie den Abstand, den zwei Strukturen mindestens haben müssen, um nach der optischen Abbildung noch als getrennte Bild-Strukturen wahrgenommen zu werden. Dabei wird beispielsweise der zur getrennten Erkennung nötige minimale Abstand zweier punktförmiger Objekte oder der minimale Abstand zwischen Linien in einem optischen Gitter betrachtet.

Rayleigh-Kriterium: zwei Beugungsscheibchen, die sich gerade noch unterscheiden lassen

Die erreichbare Auflösung ist in der klassischen Lichtmikroskopie fundamental dadurch begrenzt, dass die das Objekt umgebenden optischen Nahfelder nicht durch das optische System übertragen werden, was manchmal auch als Beugung am freien Raum bezeichnet wird. Dieser minimale Objektabstand wird als Auflösungsgrenze oder Abbe-Limit bezeichnet. Ernst Abbe hat diese Beziehung im 19. Jahrhundert beschrieben. Neuere methodische Ansätze erlauben eine Auflösung deutlich jenseits dieser Grenze, sie werden zusammenfassend als englisch Superresolution Microscopy (deutsch superauflösende Mikroskopie) bezeichnet. Derartige Techniken sind beispielsweise RESOLFT-Mikroskopie mit STED-Mikroskopie, Mikroskopie mit modulierter Beleuchtung (SIM), Photoactivated Localization Microscopy (STORM-Mikroskopie) und optisches Rasternahfeldmikroskop.

Es gibt verschiedene Ansätze, die erzielbare Auflösung zu bestimmen. Abbe ging von einem Gitter mit eng beieinander liegenden Linien aus, die von Licht durchstrahlt werden, und berechnete, wie dicht die Linien sein dürfen, so dass sie gerade noch als Linien aufgelöst werden können. Abbe untersuchte beleuchtete (passive) Objekte. John William Strutt, 3. Baron Rayleigh betrachtete punktförmige Lichtquellen. Er beschrieb den Abstand aktiver Objekte, die gerade noch als getrennt zu erkennen waren.[1] Diesem Ansatz verwandt ist die Bestimmung der Halbwertsbreite des mikroskopischen Signals einer punktförmigen Lichtquelle. Alle drei Ansätze führen rechnerisch zu sehr ähnlichen Werten für die Auflösung.[2]

Um die theoretisch mögliche Auflösung zu ermöglichen, ist es erforderlich, dass genügend Licht gesammelt wird. Bei Hellfeldmikroskopie ist dies in der Regel unproblematisch. Bei der Fluoreszenzmikroskopie können niedrige Intensitäten in Verbindung mit kurzen Belichtungszeiten dazu führen, dass zu wenige Photonen am Detektor auftreffen und der erreichte Kontrast zur getrennten Erkennung der Strukturen nicht ausreicht.

Von der Auflösung zu unterscheiden ist die Nachweisbarkeit und die erreichbare Positionierungsgenauigkeit. Mit Dunkelfeldmikroskopie, besonders der Ultramikroskopie, oder der Fluoreszenzmikroskopie lassen sich noch Partikel nachweisen, deren Größe erheblich unter der Auflösungsgrenze liegt, bei Fluoreszenzmikroskopie bis hinunter zu einzelnen Farbstoffmolekülen. Bei der Positionierungsgenauigkeit geht es darum, die Position einer Oberfläche oder eines Körpers möglichst genau im Raum zu bestimmen. Dazu kann das Helligkeitsmaximum des von einem Körper ausgehenden Lichts bestimmt werden. Dies ist mit einer Genauigkeit im Nanometerbereich möglich. In beiden Fällen unterschreitet die Auflösung jedoch nicht die Auflösungsgrenze: Es ist beispielsweise nicht möglich festzustellen, ob ausgesandtes Licht tatsächlich von einer punktartigen Struktur stammt oder von mehreren nahe beieinander liegenden.

Abbe-Limit

Herleitung und Anwendungsbereich

Mikroskopische Aufnahme eines Gitters mit 600 Linien pro Millimeter, das für Beugungsversuche verwendet werden kann.

Beugung eines Laserstrahls (von links kommend) an einem Strichgitter. Es handelt sich um ein Beispiel einer zentralen Beleuchtung, da das Gitter nicht (auch) von schräg einfallendem Licht beleuchtet wird. Ein Objektiv könnte vom Gitter nur dann ein Bild mit Strukturinformation erzeugen, wenn außer dem Hauptmaximum (gerade Fortsetzung des Laserstrahls) noch mindestens das erste Nebenmaximum (Strahlen im 20°-Winkel) aufgefangen wird.

Der halbe Öffnungswinkel α eines Objektivs. Hier beträgt der Wert etwa α = 50°. Für ein Trockenobjektiv ergibt das eine numerische Apertur von sin 50° = 0,77.

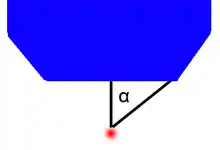
Ernst Abbe untersuchte das Beugungsverhalten des Lichts an Strichgittern. Je dichter die Striche des (optischen) Gitters beieinander liegen (also je mehr Linien auf einen Millimeter kommen), desto stärker wird hindurch tretendes Licht gebeugt. Es wird zunächst der Fall betrachtet, dass das Licht (nur) senkrecht auf die Rückseite des Gitters auftrifft (zentrale Beleuchtung). Um Informationen über die abzubildende Gitterstruktur zu erhalten, muss außer dem gerade (senkrecht) durch das Gitter hindurch tretenden Hauptmaximum des Beugungsmusters auch mindestens das erste Nebenmaximum aufgefangen werden. Die Öffnung (genauer: der Öffnungswinkel) des Objektivs muss hierfür ausreichend groß sein. Liegen die Striche des Gitters so dicht beieinander, dass das erste Nebenmaximum nicht mehr vom Objektiv aufgefangen werden kann, wird die Gitterstruktur demnach nicht mehr aufgelöst.[2]

Abbe schrieb über diese Zusammenhänge 1873 in seinem Werk „Beiträge zur Theorie des Mikroskops und der mikroskopischen Wahrnehmung“[3]:

„[…] die physikalische Unterscheidungsgrenze […] hängt allein vom Oeffnungswinkel ab und ist dem Sinus seines halben Betrages proportional.“

– Abbe, 1873, S. 466

und an anderer Stelle genauer:

„Da nun auch beim Immersionssystem der Oeffnungswinkel durch kein Mittel erheblich über diejenige Grösse, die 180° in Luft entsprechen würde, hinausgeführt werden kann, so folgt, dass […] die Unterscheidungsgrenze für centrale Beleuchtung doch niemals über den Betrag der ganzen, und für äusserste schiefe Beleuchtung niemals über den der halben Wellenlänge des blauen Lichts um ein Nennenswerthes hinausgehen wird.“

– Abbe, 1873, S. 456

„Schiefe Beleuchtung“ meint hier eine Beleuchtung mit Kondensor, der bewirkt, dass das Licht als Strahlkegel auf das Präparat auftrifft und nicht als Zylinder wie bei zentraler Beleuchtung. Eine korrekte Beleuchtung, die auch schräg einfallendes Licht einschließt, ist zum Erreichen der maximal möglichen Auflösung wesentlich. Außerdem zeigt sich die Bedeutung der Wellenlänge: Da kurzwelliges (blaues) Licht weniger stark gebeugt wird als langwelliges (rotes), kann mit kurzwelligem Licht eine bessere Auflösung erreicht werden. Das Abbe-Kriterium ist absolut, es kann mit klassischer Mikroskopie nicht überwunden werden.[4]

Die abbeschen Überlegungen zur Bildentstehung gelten für Fälle, in denen einfallendes Licht vom Präparat gebeugt wird und dann weiter zum Detektor geleitet wird. Da die Beleuchtung von einer Lichtquelle kommt, kann sie als kohärent angesehen werden. Für selbstleuchtende Objekte machen Abbes Überlegungen keine Aussagen. Auch für die Auflösung entlang der optischen Achse (z-Richtung) wird keine Angabe gemacht.[5]

Formeln

Für alle Formeln gilt: $d$ ist die erzielbare Auflösung, genauer: der Abstand, den zwei Linien in einem Gitter mindestens haben müssen, damit sie im Mikroskop noch als getrennte Linien erkannt werden können.

Zentrale Beleuchtung

Für den Fall einer ausschließlich zentralen Beleuchtung ohne Kondensor ergibt sich

d={\frac {\lambda }{n\sin \alpha }}

oder, da $n\cdot \sin \alpha$ die numerische Apertur (NA) ist,

d={\frac {\lambda }{\mathrm {NA_{Objektiv}} }}

.

mit λ der Wellenlänge des verwendeten Lichts, n dem Brechungsindex des Immersionsmediums und α dem halben Öffnungswinkel des Objektivs.

Objektiv mit kleinerer NA als Kondensor

Abbe-Denkmal in Jena mit der Auflösungsformel im oberen Bereich.

Die von Abbe erwähnte „äußerste schiefe Beleuchtung“ bezeichnet einen Durchlicht-Strahlengang, bei dem zur Beleuchtung ein Kondensor eingesetzt wird, der mindestens den gleichen Öffnungswinkel beziehungsweise mindestens die gleiche numerische Apertur hat wie das Objektiv. Für diesen Fall ergibt sich die Abbe’sche Formel in ihrer wohl bekanntesten Form:

d={\frac {\lambda }{2n\sin \alpha }}

oder, wegen $n\cdot \sin \alpha =\mathrm {NA}$ verkürzt

d={\frac {\lambda }{2\mathrm {NA} }}

Objektiv mit größerer oder gleich großer NA wie Kondensor

Wenn die numerische Apertur von Kondensor und Objektiv gleich groß sind ergibt sich ein praktisches Problem: Der Bildkontrast ist sehr niedrig. Ein optimaler Bildkontrast stellt sich ein, wenn die numerische Apertur des Kondensors bei 2/3 der numerischen Apertur des Objektivs liegt. Gegebenenfalls kann die Kondensorblende (= Aperturblende) zugezogen werden, um dies zu erreichen. Unter der Bedingung, dass die Kondensorapertur kleiner ist als die Objektivapertur gilt folgende Formel:[5]

d={\frac {\lambda }{\mathrm {NA_{Objektiv}} +\mathrm {NA_{Kondensor}} }}

Diese Fassung kann auch als allgemeine Form angesehen werden, da bei zentraler Beleuchtung gilt $\mathrm {NA_{Kondensor}} =0$ und sich bei gleich großen Aperturen wiederum 2NA unter dem Bruchstrich ergibt.

Beispiele

Objektiv mit NA 0,25 (bei vielen 10x-Objektiven); Kondensor mit NA 0,55, gelb-grünes Licht mit 550 nm, da das Auge für diesen Farbbereich am empfindlichsten ist.

d={\frac {550\,{\text{nm}}}{2\cdot 0{,}25}}=1100\,{\text{nm}}

Die Kondensorapertur kann maximal mit dem gleichen Wert eingehen wie die Objektivapertur, daher wird im Fall einer größeren Kondensorapertur die Objektivapertur mal zwei genommen.

Objektiv mit NA 0,65 (bei vielen 40x-Objektiven); Kondensor mit 0,55, Licht mit 550 nm.

d={\frac {550\,{\text{nm}}}{0{,}65+0{,}55}}=450\,{\text{nm}}

Ölimmersionsobjektiv mit NA 1,4 und Ölimmersionskondensor mit 1,4, Licht mit 550 nm

d={\frac {550\,{\text{nm}}}{1{,}4+1{,}4}}=196\,{\text{nm}}

Rayleigh-Kriterium

Helligkeitsverteilung bei zwei nah beieinander liegenden leuchtenden Punkten. A: Der Abstand entspricht etwa der Halbwertsbreite, die Punkte können nicht aufgelöst werden. B: Sparrow Limit, ein nachweisbarer Helligkeitsabfall zwischen den Maxima. C: Rayleigh-Kriterium, das Maximum eines Punktes liegt im ersten Minimum des anderen. D: Die Punkte sind deutlich voneinander getrennt.

Beugungsscheibchen. Um das helle Zentrum liegen Ringe, die zunehmend schwächer werden.

Herleitung und Anwendungsbereich

Für die Auflösung selbstleuchtender Strukturen, wie sie unter anderem in der Fluoreszenzmikroskopie auftreten, gelten die hier aufgeführten Gesetzmäßigkeiten. Die Erstbeschreibung dieser Regeln für die Mikroskopie wird je nach Lehrbuch entweder[4] auf eine Arbeit von 1896[6] von John William Strutt, 3. Baron Rayleigh, zurückgeführt, oder auf Rayleigh und Hermann von Helmholtz[7][8] oder nur auf Arbeiten von Helmholtz[9][10] von 1873 oder 1874. In allen Fällen wird das entsprechende Kriterium als Rayleigh-Kriterium bezeichnet, das aus der Astronomie bzw. vom Teleskop auf das Mikroskop übertragen wurde.

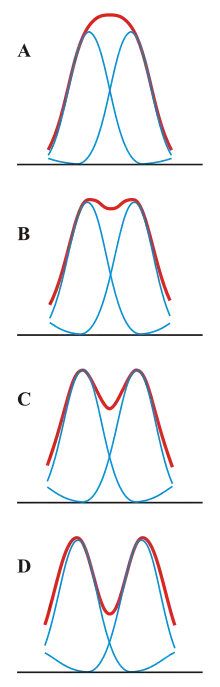
Mikroskopische Bilder selbstleuchtender Punkte sind keine Punkte, sondern Beugungsmuster, deren Helligkeitsverteilung von der Punktspreizfunktion abhängt. Diejenige Ebene des Musters, welche die höchste Intensität enthält (Schärfeebene), wird als Beugungsscheibchen bezeichnet. Das Rayleigh-Kriterium besagt, dass sich zwei selbstleuchtende Punkte, die nebeneinander in der Schärfeebene liegen, dann gerade noch unterscheiden lassen, wenn das Intensitätsmaximum des Beugungsscheibchens des ersten Punktes in das Minimum des Beugungsscheibchens des zweiten Punktes fällt (siehe Abbildung). Die Helligkeit der dunkelsten Stelle zwischen den beiden Maxima beträgt dann 73,5 % der Maxima. Beim Rayleigh-Kriterium handelt es sich also um eine Konvention und nicht um ein absolutes Kriterium, da manche Beobachter vielleicht auch noch Beugungsscheibchen unterscheiden können, die noch dichter zusammen liegen.[4][11]

Formel

Die in diesem Abschnitt aufgeführten Formeln gelten für selbstleuchtende Punkte bei Beobachtung mit klassischer Mikroskopie, beispielsweise in der klassischen Fluoreszenzmikroskopie. Für konfokale Mikroskopie und Multiphotonen-Anregung siehe die entsprechenden Abschnitte.

Auch beim Rayleigh-Kriterium geht die Wellenlänge ein, jedoch nicht wie beim Abbe-Limit die von am Objekt gebeugten Licht, sondern die Wellenlänge des vom Objekt abgestrahlten Lichts, bei Fluoreszenzmikroskopie also die Wellenlänge der Fluoreszenz.[2]

Die Auflösung (Rayleigh-Kriterium) in der Fokusebene beträgt

d={\frac {0{,}61\lambda }{\mathrm {NA} }}

, manchmal auch angegeben in der Form

d={\frac {1{,}22\lambda }{2\mathrm {NA} }}

,

wobei NA die numerische Apertur des verwendeten Objektivs ist und λ die Wellenlänge des emittierten Lichtes.[12]

Axiale Auflösung

Die Auflösung eines Mikroskops ist entlang der optischen Achse (z-Richtung) generell schlechter als innerhalb der Fokusebene. Für selbstleuchtende Punkte (klassische Fluoreszenzmikroskopie) kann wie beim Rayleigh-Kriterium auch entlang der optischen Achse der Abstand berechnet werden, der zwischen dem Helligkeitsmaximum des Beugungsmusters und dem ersten Minimum entlang der optischen Achse liegt. Auf Grund der zugrunde liegenden theoretischen Annahmen gilt die sich ergebende Formel aber nur für paraxiale Optik, also für Objektive mit kleinen Öffnungswinkeln und niedriger numerischer Apertur.[13]

d={\frac {2\lambda n}{\mathrm {NA} ^{2}}}

wobei $n$ der Brechungsindex des Mediums zwischen Objektiv und Deckglas oder Präparat ist, also zum Beispiel 1 für Luft bei Trockenobjektiven oder 1,518 für typisches Immersionsöl. Eine Bestimmung der Intensitätsverteilung für Objektive mit höherer numerischer Apertur kann unter Anwendung der Fresnel-Huygens-Theorie erreicht werden, wobei weniger Annahmen erforderlich sind und somit eine realistischere Verteilung resultiert.[13]

Während die laterale Auflösung bei Objektiven mit gleicher numerischen Apertur immer gleich ist, ergibt sich aus dieser Formel, dass Immersionsobjektive in axialer Richtung bei gleicher numerischen Apertur eine schlechtere Auflösung haben, da der Brechungsindex n des Immersionsmediums hier auch über dem Bruchstrich eingeht. Da Immersionsobjektive jedoch meistens eine höhere numerische Apertur haben als Trockenobjektive, kommt dieser Aspekt selten zum Tragen, da eine höhere numerische Apertur im Quadrat zu einer Verbesserung der Auflösung beiträgt.[13]

Halbwertsbreite

Idealisierte Helligkeitsverteilung durch das Beugungsscheibchen eines punktförmigen fluoreszierenden Objektes (rot) mit eingezeichneter Halbwertsbreite (blau)

Herleitung und Anwendungsbereich

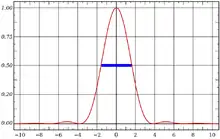
Die Auflösung nach dem Rayleigh-Kriterium lässt sich zwar berechnen, aber experimentell nur schwer bestimmen: Zwei sehr kleine Objekte müssten immer näher zusammengeschoben werden, bis sie nicht mehr unterscheidbar wären. Aus praktischen Gründen behilft man sich in der Fluoreszenzmikroskopie daher mit der Halbwertsbreite (engl.: full width half maximum, FWHM) der Punktspreizfunktion (engl. point spread function, PSF). Die Punktspreizfunktion beschreibt das durch Beugung zu Stande kommende dreidimensionale Abbild eines fluoreszenten Punktes, sie ist eine Funktion des optischen Systems, im Wesentlichen des Objektivs. Sie kann ebenfalls berechnet werden.[14] Für die experimentelle Bestimmung werden fluoreszierende Objekte eingesetzt, deren Größe unter der Auflösungsgrenze liegt, beispielsweise 150 Nanometer kleine, mit Fluoreszenzfarbstoff getränkte Latexkügelchen oder Quantenpunkte. Gemessen wird die Halbwertsbreite der Intensitätskurve in Nanometern oder Mikrometern (siehe Abbildung). Auflösung und Halbwertsbreite der PSF stehen in einer mathematischen Beziehung zueinander, die PSF-Halbwertsbreite liegt bei etwas kleineren Werten als die Auflösung.[15]

Formeln

Die in diesem Abschnitt aufgeführten Formeln gelten für selbstleuchtende Punkte bei Beobachtung mit klassischer Mikroskopie, beispielsweise in der klassischen Fluoreszenzmikroskopie. Für konfokale Mikroskopie und Multiphotonen-Anregung siehe die entsprechenden Abschnitte.

In x,y-Richtung liegt die Halbwertsbreite der PSF bei

\mathrm {FWHM} _{\text{(x,y)}}={\frac {0{,}51\lambda }{\mathrm {NA} }}

wobei NA die numerische Apertur des verwendeten Objektivs ist und λ die Wellenlänge des emittierten Lichtes.[12]

Entlang der optischen Achse (z-Richtung) liegt die Halbwertsbreite der PSF bei

\mathrm {FWHM} _{z}={\frac {0{,}88\lambda }{n-{\sqrt {n^{2}-\mathrm {NA} ^{2}}}}}

.[12]

Diese Formel kann bei numerischen Aperturen unter 0,5 verkürzt werden auf

\mathrm {FWHM} _{z}={\frac {1{,}77n\lambda }{\mathrm {NA} ^{2}}}

.[12]

Beispiel

Für ein Ölimmersionsobjektiv mit einer numerischen Apertur von 1,4 und bei einer Wellenlänge von 550 nm ergibt sich in der Fokusebene (x,y) eine Halbwertsbreite von

\mathrm {FWHM} _{\text{(x,y)}}={\frac {0{,}51\cdot 550\,{\text{nm}}}{1{,}4}}=200\,{\text{nm}}

Entlang der optischen Achse bei Verwendung eines Immersionsöls mit dem Brechungsindex n=1,518 ergibt sich

\mathrm {FWHM} _{z}={\frac {0{,}88\cdot 550\,{\text{nm}}}{1{,}518-{\sqrt {1{,}518^{2}-1{,}4^{2}}}}}=520\,{\text{nm}}

Steigerung der Auflösung in der klassischen Mikroskopie

Sowohl aus dem Abbe-Limit als auch aus dem Rayleigh-Kriterium ergibt sich, dass die Auflösung hin zu kleineren Werten auf zwei Wegen gesteigert werden kann: Durch Verkleinerung der Wellenlänge λ und durch Vergrößerung der numerischen Apertur NA.

Verkürzung der Wellenlänge

Der Ansatz der Verkleinerung der Wellenlänge führte Anfang des 20. Jahrhunderts zur Entwicklung der UV-Mikroskopie, bei der UV-Licht statt sichtbarem Licht eingesetzt wurde. August Köhler entwickelte entsprechende Geräte ab 1900 bei Zeiss. Damit ließ sich die Auflösung bei einer verglichen mit sichtbarem Licht halbierter Wellenlänge auf das Doppelte steigern. Da das menschliche Auge dieses Licht nicht wahrnehmen kann, ist eine Darstellung nur mittels Film oder Fluoreszenzschirmen möglich. Außerdem müssen Linsen, Objektträger und so weiter aus Quarzglas, Flussspat oder Lithiumfluorid hergestellt werden, da normales Glas UV-Licht absorbiert. Auf Grund dieser Schwierigkeiten konnte sich die UV-Mikroskopie nicht generell durchsetzen und blieb Spezialanwendungen vorbehalten.[16][17][18]

Als Nebeneffekt der Versuche von Köhler wurde die Möglichkeit der Fluoreszenzmikroskopie entdeckt, da einige untersuchte Stoffe bei Anregung mit UV-Licht fluoreszierten.[18]

Steigerung der numerischen Apertur

Die numerische Apertur NA ist das Produkt aus n, dem Brechungsindex des Mediums zwischen Präparat und Objektiv, und sinα, dem Sinus des halben Öffnungswinkels. Um NA zu vergrößern muss also einer der beiden Faktoren vergrößert werden. Angenommen ein Objektiv hätte eine unendlich große Frontlinse, dann wäre der Öffnungswinkel 180°, der halbe Öffnungswinkel demnach 90° und dessen Sinus also 1. Da die Frontlinse des Objektivs aber endlich groß ist und auch ein gewisser Arbeitsabstand zwischen Schärfeebene und Frontlinse erforderlich ist, ist sinα immer kleiner als 1. Hochwertige Objektive können Werte von 0.95 erreichen.[18]

Der Brechungsindex kann gesteigert werden, indem Immersion eingesetzt wird, also eine Flüssigkeit zwischen Präparat und Objektiv eingebracht wird. Hierfür sind für verschiedene Immersionsmedien jeweils spezielle Objektive notwendig, deren Linsen so berechnet wurden, dass sie dem veränderten Brechungsverhalten vor dem Objektiv angepasst sind. Während Luft einen Brechungsindex von etwa 1 hat, liegt der von Wasser bei 1,33 und der von typischem Immersionsöl bei 1,518. Entsprechend kann die Auflösung mit Ölimmersion um über 50 % gegenüber immersionsfreier Mikroskopie gesteigert werden.

Die höchsten numerischen Aperturen mit weiterer Verbreitung liegen daher bei NA=1,4 für Ölimmersionsobjektive mit einer Vergrößerung von 100× oder 60×. Auch Ölimmersionskondensoren können NA=1,4 erreichen. Einen noch höheren Brechungsindex als Öl hat Monobromnaphthalin mit n=1,666, das Ernst Abbe in die Mikroskopie einführte. Entsprechende Objektive erreichten eine NA von 1,63. Sie waren jedoch nicht für die Durchlichtmikroskopie biologischer Objekte geeignet, da zu ihrer Verwendung auch Objektträger, Deckgläser, Einbettmedium sowie das eigentliche Objekt einen mindestens gleich hohen Brechungsindex hätten aufweisen müssen.[16][19][18]

Höhere numerische Aperturen als 1,4 finden sich heute mit 1,45 bei speziellen Ölimmersionsobjektiven für die TIRF-Mikroskopie.

Konfokale Fluoreszenzmikroskopie

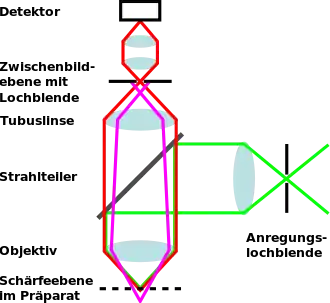
Schemazeichnung des konfokalen Prinzips. Von den Lichtkegeln sind nur die jeweiligen Randstrahlen eingezeichnet, die von den optischen Elementen gerade noch aufgenommen werden. Durch die Anregungslochblende entsteht eine punktförmige Lichtquelle, deren Abbild die Beleuchtungs-PSF darstellt.

Bei der konventionellen Fluoreszenzmikroskopie wird die Probe großflächig beleuchtet und durch das Objektiv abgebildet, so dass die PSF des Gesamtsystems nur durch die (Detektions-)PSF des Objektivs bestimmt ist. Im Gegensatz dazu wird die Probe im Konfokalmikroskop mit dem Beugungsscheibchen (genauer: der Punktspreizfunktion) der Beleuchtungslochblende beleuchtet. In diesem Fall wird die Auflösung des Gesamtsystems also durch die Multiplikation zweier Punktspreizfunktionen bestimmt, nämlich der Beleuchtungs-PSF und der Detektions-PSF.

Auflösung in der Fokusebene (x, y)

Durch die PSF-Multiplikation ändert sich der Durchmesser des Beugungsscheibchens nicht, das erste Minimum ist noch an der gleichen Stelle wie zuvor. Allerdings ist der Helligkeitsanstieg nun steiler, die Flanken der Helligkeitsverteilung rücken nach innen. Zwei solcher multiplizierten Beugungsscheibchen liegen daher dichter beieinander, wenn die minimale Intensität zwischen den Maxima die oben beim Rayleigh-Kriterium erwähnten 73,5 % erreicht, man spricht dann vom verallgemeinerten Rayleigh-Kriterium[20]. Theoretisch ergibt sich dadurch eine Verbesserung der Auflösung um den Faktor ${\tfrac {1}{\sqrt {2}}}$ , also etwa ${\tfrac {1}{1{,}4}}$ .[11][21]

In der Fokusebene ergäbe sich für die Halbwertsbreite des Signals eines fluoreszierenden punktförmigen Objekts ${\tfrac {0{,}51\lambda }{{\sqrt {2}}\cdot \mathrm {NA} }}$ oder ${\tfrac {0{,}37\lambda }{\mathrm {NA} }}$ , wobei bei Fluoreszenz als Wellenlänge der Mittelwert von Anregungs- und Emissionswellenlänge einzusetzen ist. Bei grünem Licht (Wellenlänge 500 nm) entspricht dies bei einem Ölimmersionsobjektiv mit 1,4 numerischer Apertur einer Halbwertsbreite von 132 nm (nicht-konfokal: 182 nm). Jedoch kann dieser Wert nur theoretisch, bei unendlich kleiner Lochblende erreicht werden, bei der also kein Licht mehr aufgefangen werden würde. Auch wird vorausgesetzt, dass das anregende Licht das Objektiv von der Rückseite her vollständig ausfüllt. Dies ist jedoch nicht immer der Fall.[21][12]

Die praktisch erzielbare Verbesserung ist daher geringer. Sie hängt davon ab, wie viel des Beugungsscheibchens von der Lochblendenöffnung durchgelassen wird, also vom Durchmesser der Lochblende. Liegt der Lochblendendurchmesser im ersten Minimum des Beugungsscheibchens, so ist die Auflösung in der Fokusebene nicht mehr besser als im nicht-konfokalen Fall, wogegen die Signalintensität dann schon fast maximal ist. Der Ausschluss von Fluoreszenz aus anderen Ebenen funktioniert jedoch noch recht gut.[20] Daher ist dieser Wert bei kommerziellen Konfokalmikroskopen häufig voreingestellt. Er wird als eine Airy unit (AU) bezeichnet, nach den englischen Begriffen Airy disk (= Beugungsscheibchen) und unit (= Maßeinheit).[12]

Auflösung entlang der optischen Achse

Auch hier gibt sich wie in der Fokusebene theoretisch eine Verbesserung um den Faktor ${\frac {1}{\sqrt {2}}}$ , also für die Halbwertsbreite der PSF eines fluoreszierenden Punktobjekts ${\frac {0{,}64\lambda }{n-{\sqrt {n^{2}-\mathrm {NA} ^{2}}}}}$

Die Wellenlänge ist wiederum der Mittelwert von Anregungslicht und Fluoreszenzlicht.

Eine dünne fluoreszierende Schicht hat für die Halbwertsbreite eine ähnliche, aber etwas andere Gleichung:

{\frac {0{,}67\lambda }{n-{\sqrt {n^{2}-\mathrm {NA} ^{2}}}}}

.[12]

Es ergeben sich für diese theoretische Auflösungsverbesserung die gleichen praktischen Einschränkungen, die im vorigen Abschnitt schon für die Auflösungsverbesserung in der Fokusebene beschrieben wurden.[12]

Multi-Photonen-Anregung

Eine Anregung mit zwei Photonen kommt bei der Zwei-Photonen-Fluoreszenzmikroskopie und bei der Second Harmonic Generation-Mikroskopie vor, siehe Multiphotonenmikroskop. Ähnlich wie bei der Konfokalmikroskopie wird die Auflösung daher durch die Multiplikation zweier Punktspreizfunktionen (PSF) bestimmt, nur dass es sich hier zweimal um die Anregungs-PSF handelt. Es kommt also wiederum eine Verbesserung um den Faktor $1/{\sqrt {2}}$ . Da bei der Multiphotonenanregung im Gegensatz zur Konfokalmikroskopie keine Lochblende eingesetzt wird, entfällt die entsprechende Einschränkung, und die verbesserte Auflösung ist hier tatsächlich möglich. Die Größe der PSF ist dabei ausschließlich von der Anregungswellenlänge abhängig. Da jedoch bei diesen Techniken in der Regel Anregungswellenlängen von 800 nm oder mehr eingesetzt werden, ergibt sich gemessen in Mikrometern keine bessere Auflösung als in der klassischen Fluoreszenz oder Konfokalmikroskopie. Wie bei der Konfokalmikroskopie ist es auch hier für die maximale Auflösung erforderlich, dass der anregende Laserstrahl das Objektiv von der Rückseite her vollständig ausfüllt.[21]

Für die Halbwertsbreite der PSF in der Fokusebene (x,y) ergibt sich

{\frac {0{,}51\lambda }{{\sqrt {2}}\cdot \mathrm {NA} }}

beziehungsweise

{\frac {0{,}37\lambda }{\mathrm {NA} }}

[21]

und dadurch zum Beispiel für eine Zwei-Photonen-Fluoreszenz-Anregung mit einem Wasserimmersionsobjektive mit NA = 1,1

{\frac {0{,}37\cdot 800\,{\text{nm}}}{1{,}1}}=269\,{\text{nm}}

wogegen sich bei einer normalen, Ein-Photonen-Fluoreszenz-Anregung für den gleichen Farbstoff mit dem gleichen Objektiv nach den weiter oben aufgeführten Formeln zum Beispiel ergeben könnte

{\frac {0{,}51\cdot 510\,{\text{nm}}}{1{,}1}}=236\,{\text{nm}}

Auch entlang der optischen Achse (z-Richtung) können die Formeln angewendet werden, die oben für ein Konfokalmikroskop mit geschlossener Lochblende angegeben wurden.

Bei einer Anregung mit drei Photonen, also bei Drei-Photonen-Fluoreszenzmikroskopie und bei der Third-Harmonic-Generation-Mikroskopie, kommt es zu einer Verbesserung um den Faktor ${\tfrac {1}{\sqrt {3}}}$ . Bei gleicher Anregungswellenlänge ergibt sich also für Drei-Photonen-Anregung eine bessere Auflösung als für Zwei-Photonen-Anregung. Die Formel für die Halbwertsbreite der PSF in der Fokusebene (x,y) ist

{\frac {0{,}51\lambda }{{\sqrt {3}}\cdot \mathrm {NA} }}

beziehungsweise

{\frac {0{,}29\lambda }{\mathrm {NA} }}

[22]

Kontrast

Die theoretisch mögliche Auflösung nach den oben angegebenen Formeln lässt sich nur dann realisieren, wenn der Kontrast zwischen den hellen und dunklen Objekten hoch genug ist, so dass diese auch tatsächlich unterschieden werden können. Dies kann beispielsweise bei der Hellfeldmikroskopie von ungefärbten biologischen Präparaten zum Problem werden, wenn diese kaum Licht absorbieren. Der Kontrast kann hier in vielen Fällen verbessert werden, wenn kontraststeigernde Methoden wie Dunkelfeldmikroskopie, Phasenkontrast oder Differentialinterferenzkontrast eingesetzt werden.

Speziell bei fluoreszenzmikroskopischen Anwendungen kann das Problem auftreten, dass die erzeugte Fluoreszenz sehr lichtschwach ist und daher eine gewisse Belichtungszeit nicht unterschritten werden darf, um genügend Photonen zu sammeln, um den erforderlichen Mindestkontrast beziehungsweise ein ausreichendes Signal-Rausch-Verhältnis zu erzielen. In der Hellfeldmikroskopie ist dies auf Grund der verwendeten relativ hohen Lichtintensitäten in der Regel kein Problem; das Phänomen lässt sich jedoch künstlich nachstellen, indem die Belichtungsstärke stark abgesenkt wird (siehe Abbildung).

Serie abnehmender Belichtungszeiten bei sehr geringer Beleuchtungsintensität. Lichtdurchlässige Balkengruppen wurden bei Durchlicht-Hellfeld-Mikroskopie von einer CCD-Kamera aufgenommen. Die Helligkeit der einzelnen Aufnahmen wurde nachträglich angeglichen, um eine gleichzeitige Darstellung zu ermöglichen. Das Signal-Rausch-Verhältnis wird mit abnehmender Belichtungszeit immer schlechter. Einerseits tritt im CCD-Chip konstantes Dunkelrauschen und Ausleserauschen auf (siehe Bildrauschen), andererseits setzt sich das eigentliche Signal aus einzelnen Photonen zusammen, von denen in einem statistischen Prozess genügend detektiert werden müssen, um vom CCD-Rauschen unterscheidbar zu sein. Das Auftreffen der einzelnen Photonen wird als Schrotrauschen beschrieben. In diesem Beispiel reicht bei 3 Millisekunden Belichtungszeit der Kontrast gerade noch aus, um die größeren Balken zu erkennen. Von den kleinsten Balkengruppen im Präparat gelangen jedoch nicht mehr genügend Photonen zur Kamera, um die Balken sichtbar zu machen und damit aufzulösen. Bei einer Millisekunde sind keine Balken mehr erkennbar. Werden aber 100 Bilder mit 1 ms Belichtungszeit zusammenaddiert, tauchen die Balken wieder auf, dann fließen insgesamt genügend Photonen ein, um das Signal vom Kamerarauschen zu unterscheiden. Das Summenbild ist verrauschter als eine einzelne Belichtung mit 100 ms, da das Ausleserauschen hundertmal einfloss.

Digitalisierung der maximalen Auflösung: Das Nyquist-Kriterium

Wenn mikroskopische Bilder digitalisiert werden, kann die optisch erzielte Auflösung nur dann erhalten werden, wenn im digitalen Bild die Bildpunkte (Pixel) dicht genug beieinander liegen. Stellt man sich zwei getrennt nebeneinander liegende helle Punkte vor, so können diese nur dann auch im digitalen Bild getrennt dargestellt werden, wenn zwischen ihnen vereinfacht gesprochen noch ein dunkleres Pixel liegt: Es kämen daher drei Pixel auf den minimal darstellbaren Abstand, zwei für die hellen Punkte und ein dunkles dazwischen. Tatsächlich sagt das Nyquist-Kriterium aus, dass für den kleinsten optisch darstellbaren Abstand 2,3 Pixel erforderlich sind. Wenn also beispielsweise die optisch erzielbare Auflösung bei 230 nm liegt, muss demnach die Größe der Pixel bei 100 nm liegen. Eine etwas genauere Abtastung, also etwas kleinere Pixel, kann in der Praxis gerechtfertigt sein, um kleine Unterschiede besser sichtbar zu machen. Ein Abtasten mit mehr als 3 Pixeln (Überabtastung) bringt jedoch keine weiteren Vorteile mehr. Die Bilddatei würde aber unnötig groß. Bei fluoreszenzmikroskopischen Anwendungen kommt hinzu, dass die Fluoreszenzfarbstoffe durch die einhergehende stärkere Beleuchtung unnötig schnell ausbleichen. Auch andere mikroskopische Präparate, die empfindlich auf starke Beleuchtung reagieren, können unnötig geschädigt werden.[23]

Das Nyquist-Kriterium gilt sowohl für die Fokusebene (x,y) als auch entlang der optischen Achse (z-Richtung). Unerheblich ist die Art der Digitalisierung, beispielsweise als parallele Rasterdetektion mittels einer CCD/CMOS-Kamera oder mit Hilfe eines schnellen Photodetektors und einem Scanner bei rasternden Verfahren.

Experimentelle Überprüfung der erzielbaren Auflösung

Insbesondere bei superauflösenden Techniken (z. B. STED oder STORM) lässt sich die real erzielbare Auflösung nicht immer auf einfache Weise aus der Theorie ableiten. Es gibt jedoch einige Möglichkeiten, diese experimentell zu bestimmen. Die zurzeit am weitesten verbreitete Methode dafür verwendet Strukturen des eukaryontischen Zytoskeletts, da sich mit diesen sehr eindrucksvolle Bilder erzielen lassen. Dabei wird das erhaltene Bild nach eng benachbarten, möglichst parallel verlaufenden Filamenten durchsucht und deren Abstand zueinander bestimmt. Der kleinste dabei gefundene Wert wird als erzielte Auflösung gewertet.[24][25]

Eine andere Möglichkeit basiert auf der Verwendung von Nanometerlinealen. Dieses sind auf DNA basierende Nanostrukturen, die Farbstoffmoleküle in genau definierten Abständen zueinander tragen. Sie ermöglichen somit eine weniger willkürliche und deutlich systematischere Bestimmung der optischen Auflösung.[25]

Siehe auch

Schrägbeleuchtung

Einzelnachweise

Hermann Strass: Das Abbe-Limit überwinden. In: GIT Labor-Fachzeitschrift. Januar 2016, S. 11.
Christoph Cremer: Lichtmikroskopie unterhalb des Abbe-Limits. Lokalisationsmikroskopie. In: Physik in unserer Zeit. 42, Nr. 1, 2011, S. 21–29, doi:10.1002/piuz.201101251.
Ernst Abbe: Beiträge zur Theorie des Mikroskops und der mikroskopischen Wahrnehmung. In: Archiv für mikroskopische Anatomie. Band 9, Nr. 1, Dezember 1873, S. 413–468, doi:10.1007/BF02956173, urn:nbn:de:hebis:30-1123587 (Beim Verlag in 4 Segmente aufgeteilt, vgl. doi:10.1007/BF02956174, doi:10.1007/BF02956175 und doi:10.1007/BF02956176).
Guy Cox: Optical Imaging Techniques in Cell Biology. 1. Auflage. CRC Press, Taylor & Francis Group, Boca Raton FL 2006, ISBN 0-8493-3919-7, S. 8–15.
Gerhard Göke: Moderne Methoden der Lichtmikroskopie. Vom Durchlicht-Hellfeld- bis zum Lasermikroskop. Kosmos Gesellschaft der Naturfreunde Franckh’sche Verlagsbuchhandlung, Stuttgart 1988, ISBN 3-440-05765-8, S. 47–50.
John William Strutt, 3. Baron Rayleigh: On the theory of optical images, with special reference to the microscope. In: Philosophical Magazine Series 5. Band 42, Nr. 255, 1896, ISSN 1941-5982, S. 167–195, doi:10.1080/14786449608620902.
Eugene Hecht: Optik. 5. Auflage. Oldenbourg Verlag, München 2009, ISBN 978-3-486-58861-3, S. 763 f. (englisch: Optics. 4th edition. Übersetzt von Anna Schleitzer).
Randy O. Wayne: Light and Video Microscopy. Academic Press, Elesevier, 2009, ISBN 978-0-12-374234-6, S. 62.
Heinz Niedrig (Hrsg.): Optik. Wellen- und Teilchenoptik (= Bergmann Schaefer Lehrbuch der Experimentalphysik. Band 3). 10. Auflage. Walter de Gruyter, Berlin 2004, ISBN 3-11-017081-7, S. 372.
Wolfgang Zinth, Ursula Zinth: Optik. Lichtstrahlen – Wellen – Photonen. 4. Auflage. Oldenbourg Verlag, München 2013, ISBN 978-3-486-72136-2, S. 205.
Guy Cox: Optical Imaging Techniques in Cell Biology. 1. Auflage. CRC Press, Taylor & Francis Group, Boca Raton FL 2006, ISBN 0-8493-3919-7, S. 57–75.
B. Amos, G. McConnell, T. Wilson: Confocal microscopy. In: E. Egelman (Hrsg.): Biophysical Techniques for Characterization of Cells (= Comprehensive Biophysics). Band 2. Elsevier, Academic Press, Amsterdam 2012, ISBN 978-0-12-374920-8, Kapitel 2, S. 3–23, doi:10.1016/B978-0-12-374920-8.00203-4 (frei verfügbare Autorenversion: Online [abgerufen am 11. Oktober 2013]).
Ulrich Kubitscheck: Principles of Light Microscopy. In: Ulrich Kubitscheck (Hrsg.): Fluorescence Microscopy. From Principles to Biological Applications. Wiley-VCH Verlag, Weinheim, Deutschland 2013, ISBN 978-3-527-32922-9, S. 33–96 (Formel auf S. 58.).
M. J. Nasse, J. C. Woehl: Realistic modeling of the illumination point spread function in confocal scanning optical microscopy. In: J. Opt. Soc. Am. A. Vol. 27, Nr. 2, 2010, S. 295–302, doi:10.1364/JOSAA.27.000295 (englisch).
Kenneth R. Spring, Thomas J. Fellers, Michael W. Davidson: Theory of Confocal Microscopy – Resolution and Contrast in Confocal Microscopy. (Nicht mehr online verfügbar.) Archiviert vom Original am 28. Februar 2015; abgerufen am 25. April 2010 (englisch).
Dieter Gerlach: Das Lichtmikroskop. Eine Einführung in Funktion, Handhabung und Spezialverfahren für Mediziner und Biologen. Georg Thieme Verlag, Stuttgart 1976, ISBN 3-13-530301-2, S. 109–111.
Gerhard Göke: Moderne Methoden der Lichtmikroskopie. Vom Durchlicht-Hellfeld- bis zum Lasermikroskop. Kosmos Gesellschaft der Naturfreunde Franckh’sche Verlagsbuchhandlung, Stuttgart 1988, ISBN 3-440-05765-8, S. 246.
Dieter Gerlach: Geschichte der Mikroskopie. Verlag Harri Deutsch, Frankfurt am Main 2009, ISBN 978-3-8171-1781-9, S. 625 f.
Gerhard Göke: Moderne Methoden der Lichtmikroskopie. Vom Durchlicht-Hellfeld- bis zum Lasermikroskop. Kosmos Gesellschaft der Naturfreunde Franckh’sche Verlagsbuchhandlung, Stuttgart 1988, ISBN 3-440-05765-8, S. 52.
Colin J. R. Sheppard, David M. Shotton: Confocal Laser Scanning Microscopy. In: Royal Microscopical Society Microscopy Handbooks. Band 38. BIOS Scientific Publishers Limited, Oxford, UK 1997, ISBN 1-872748-72-4, S. 37, 39–42.
G. Cox, C. J. Sheppard: Practical limits of resolution in confocal and non-linear microscopy. In: Microscopy Research and Technique, Band 63, Nummer 1, 2004, S. 18–22, doi:10.1002/jemt.10423, PMID 14677129.
Jung Ho Yu, Seung-Hae Kwon, Zdenˇek Petrášek3, Ok Kyu Park, Samuel Woojoo Jun, Kwangsoo Shin, Moonkee Choi, Yong Il Park, Kyeongsoon Park, Hyon Bin Na, Nohyun Lee, Dong Won Lee, Jeong Hyun Kim, Petra Schwille, Taeghwan Hyeon: High-resolution three-photon biomedical imaging using doped ZnS nanocrystals. In: Nature Materials. 12, 2013, S. 359–366, doi:10.1038/NMAT3565.
Guy Cox: Optical Imaging Techniques in Cell Biology. 1. Auflage. CRC Press, Taylor & Francis Group, Boca Raton FL 2006, ISBN 0-8493-3919-7, S. 79 ff.
G. T. Dempsey, J. C. Vaughan, K. H. Chen, M. Bates, X. Zhuang: Evaluation of fluorophores for optimal performance in localization-based super-resolution imaging. In: Nature methods. Band 8, Nummer 12, November 2011, ISSN 1548-7091, S. 1027–1036, doi:10.1038/nmeth.1768, PMID 22056676.
J. J. Schmied, M. Raab, C. Forthmann, E. Pibiri, B. Wünsch, T. Dammeyer, P. Tinnefeld: DNA origami-based standards for quantitative fluorescence microscopy. In: Nature protocols. Band 9, Nummer 6, Juni 2014, ISSN 1750-2799, S. 1367–1391, doi:10.1038/nprot.2014.079, PMID 24833175.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Hermann Strass: Das Abbe-Limit überwinden. In: GIT Labor-Fachzeitschrift. Januar 2016, S. 11.

[Cremer-2] Christoph Cremer: Lichtmikroskopie unterhalb des Abbe-Limits. Lokalisationsmikroskopie. In: Physik in unserer Zeit. 42, Nr. 1, 2011, S. 21–29, doi:10.1002/piuz.201101251.

[Abbe1873-3] Ernst Abbe: Beiträge zur Theorie des Mikroskops und der mikroskopischen Wahrnehmung. In: Archiv für mikroskopische Anatomie. Band 9, Nr. 1, Dezember 1873, S. 413–468, doi:10.1007/BF02956173, urn:nbn:de:hebis:30-1123587 (Beim Verlag in 4 Segmente aufgeteilt, vgl. doi:10.1007/BF02956174, doi:10.1007/BF02956175 und doi:10.1007/BF02956176).

[CoxCh1-4] Guy Cox: Optical Imaging Techniques in Cell Biology. 1. Auflage. CRC Press, Taylor & Francis Group, Boca Raton FL 2006, ISBN 0-8493-3919-7, S. 8–15.

[Goke-5] Gerhard Göke: Moderne Methoden der Lichtmikroskopie. Vom Durchlicht-Hellfeld- bis zum Lasermikroskop. Kosmos Gesellschaft der Naturfreunde Franckh’sche Verlagsbuchhandlung, Stuttgart 1988, ISBN 3-440-05765-8, S. 47–50.

[6] John William Strutt, 3. Baron Rayleigh: On the theory of optical images, with special reference to the microscope. In: Philosophical Magazine Series 5. Band 42, Nr. 255, 1896, ISSN 1941-5982, S. 167–195, doi:10.1080/14786449608620902.

[7] Eugene Hecht: Optik. 5. Auflage. Oldenbourg Verlag, München 2009, ISBN 978-3-486-58861-3, S. 763 f. (englisch: Optics. 4th edition. Übersetzt von Anna Schleitzer).

[8] Randy O. Wayne: Light and Video Microscopy. Academic Press, Elesevier, 2009, ISBN 978-0-12-374234-6, S. 62.

[9] Heinz Niedrig (Hrsg.): Optik. Wellen- und Teilchenoptik (= Bergmann Schaefer Lehrbuch der Experimentalphysik. Band 3). 10. Auflage. Walter de Gruyter, Berlin 2004, ISBN 3-11-017081-7, S. 372.

[10] Wolfgang Zinth, Ursula Zinth: Optik. Lichtstrahlen – Wellen – Photonen. 4. Auflage. Oldenbourg Verlag, München 2013, ISBN 978-3-486-72136-2, S. 205.

[CoxCh5-11] Guy Cox: Optical Imaging Techniques in Cell Biology. 1. Auflage. CRC Press, Taylor & Francis Group, Boca Raton FL 2006, ISBN 0-8493-3919-7, S. 57–75.

[Amos-12] B. Amos, G. McConnell, T. Wilson: Confocal microscopy. In: E. Egelman (Hrsg.): Biophysical Techniques for Characterization of Cells (= Comprehensive Biophysics). Band 2. Elsevier, Academic Press, Amsterdam 2012, ISBN 978-0-12-374920-8, Kapitel 2, S. 3–23, doi:10.1016/B978-0-12-374920-8.00203-4 (frei verfügbare Autorenversion: Online [abgerufen am 11. Oktober 2013]).

[Kubitscheck-13] Ulrich Kubitscheck: Principles of Light Microscopy. In: Ulrich Kubitscheck (Hrsg.): Fluorescence Microscopy. From Principles to Biological Applications. Wiley-VCH Verlag, Weinheim, Deutschland 2013, ISBN 978-3-527-32922-9, S. 33–96 (Formel auf S. 58.).

[14] M. J. Nasse, J. C. Woehl: Realistic modeling of the illumination point spread function in confocal scanning optical microscopy. In: J. Opt. Soc. Am. A. Vol. 27, Nr. 2, 2010, S. 295–302, doi:10.1364/JOSAA.27.000295 (englisch).

[oly-15] Kenneth R. Spring, Thomas J. Fellers, Michael W. Davidson: Theory of Confocal Microscopy – Resolution and Contrast in Confocal Microscopy. (Nicht mehr online verfügbar.) Archiviert vom Original am 28. Februar 2015; abgerufen am 25. April 2010 (englisch).

[GerlachAufl-16] Dieter Gerlach: Das Lichtmikroskop. Eine Einführung in Funktion, Handhabung und Spezialverfahren für Mediziner und Biologen. Georg Thieme Verlag, Stuttgart 1976, ISBN 3-13-530301-2, S. 109–111.

[17] Gerhard Göke: Moderne Methoden der Lichtmikroskopie. Vom Durchlicht-Hellfeld- bis zum Lasermikroskop. Kosmos Gesellschaft der Naturfreunde Franckh’sche Verlagsbuchhandlung, Stuttgart 1988, ISBN 3-440-05765-8, S. 246.

[GeschichteUV-18] Dieter Gerlach: Geschichte der Mikroskopie. Verlag Harri Deutsch, Frankfurt am Main 2009, ISBN 978-3-8171-1781-9, S. 625 f.

[19] Gerhard Göke: Moderne Methoden der Lichtmikroskopie. Vom Durchlicht-Hellfeld- bis zum Lasermikroskop. Kosmos Gesellschaft der Naturfreunde Franckh’sche Verlagsbuchhandlung, Stuttgart 1988, ISBN 3-440-05765-8, S. 52.

[royal-20] Colin J. R. Sheppard, David M. Shotton: Confocal Laser Scanning Microscopy. In: Royal Microscopical Society Microscopy Handbooks. Band 38. BIOS Scientific Publishers Limited, Oxford, UK 1997, ISBN 1-872748-72-4, S. 37, 39–42.

[coxsheppard-21] G. Cox, C. J. Sheppard: Practical limits of resolution in confocal and non-linear microscopy. In: Microscopy Research and Technique, Band 63, Nummer 1, 2004, S. 18–22, doi:10.1002/jemt.10423, PMID 14677129.

[DOI10.1038/NMAT3565-22] Jung Ho Yu, Seung-Hae Kwon, Zdenˇek Petrášek3, Ok Kyu Park, Samuel Woojoo Jun, Kwangsoo Shin, Moonkee Choi, Yong Il Park, Kyeongsoon Park, Hyon Bin Na, Nohyun Lee, Dong Won Lee, Jeong Hyun Kim, Petra Schwille, Taeghwan Hyeon: High-resolution three-photon biomedical imaging using doped ZnS nanocrystals. In: Nature Materials. 12, 2013, S. 359–366, doi:10.1038/NMAT3565.

[CoxNy-23] Guy Cox: Optical Imaging Techniques in Cell Biology. 1. Auflage. CRC Press, Taylor & Francis Group, Boca Raton FL 2006, ISBN 0-8493-3919-7, S. 79 ff.

[natmethods-24] G. T. Dempsey, J. C. Vaughan, K. H. Chen, M. Bates, X. Zhuang: Evaluation of fluorophores for optimal performance in localization-based super-resolution imaging. In: Nature methods. Band 8, Nummer 12, November 2011, ISSN 1548-7091, S. 1027–1036, doi:10.1038/nmeth.1768, PMID 22056676.

[natureprot-25] J. J. Schmied, M. Raab, C. Forthmann, E. Pibiri, B. Wünsch, T. Dammeyer, P. Tinnefeld: DNA origami-based standards for quantitative fluorescence microscopy. In: Nature protocols. Band 9, Nummer 6, Juni 2014, ISSN 1750-2799, S. 1367–1391, doi:10.1038/nprot.2014.079, PMID 24833175.