Advanced Encryption Standard

AES
	AESDer Substitutionsschritt, einer von 4 Teilschritten pro Runde
Entwickler	Joan Daemen, Vincent Rijmen
Veröffentlicht	1998, Zertifizierung Oktober 2000
Abgeleitet von	Square
Zertifizierung	NESSIE
Schlüssellänge	128, 192 oder 256 Bit
Blockgröße	128 Bit[1]
Struktur	Substitutions-Permutations-Netzwerk
Runden	10, 12 oder 14 (schlüssellängenabhängig)
Beste bekannte Kryptoanalyse
	Der geheime Schlüssel kann bei AES-128 in Schritten, bei AES-192 in Schritten und bei AES-256 in Schritten gefunden werden.[2]

Der Advanced Encryption Standard (AES) (deutsch etwa „fortschrittlicher Verschlüsselungsstandard“) ist eine Blockchiffre, die als Nachfolger des DES im Oktober 2000 vom National Institute of Standards and Technology (NIST) als US-amerikanischer Standard bekanntgegeben wurde. Der Algorithmus wurde von Joan Daemen und Vincent Rijmen unter der Bezeichnung Rijndael entwickelt.

Es handelt sich um ein symmetrisches Verschlüsselungsverfahren, d. h. der Schlüssel zum Ver- und Entschlüsseln ist identisch. Der Rijndael-Algorithmus besitzt variable, voneinander unabhängige Block- und Schlüssellängen von 128, 160, 192, 224 oder 256 Bit. Rijndael bietet ein sehr hohes Maß an Sicherheit; erst mehr als zehn Jahre nach seiner Standardisierung wurde der erste theoretisch interessante, praktisch aber nicht relevante Angriff gefunden.

AES schränkt die Blocklänge auf 128 Bit und die Wahl der Schlüssellänge auf 128, 192 oder 256 Bit ein. Die Bezeichnungen der drei AES-Varianten AES-128, AES-192 und AES-256 beziehen sich jeweils auf die gewählte Schlüssellänge. AES ist frei verfügbar und darf ohne Lizenzgebühren eingesetzt sowie in Soft- und Hardware implementiert werden.

Das Verfahren ist pragmatisch sicher, das heißt, es ist kein praktisch durchführbarer Angriff bekannt. Es ist jedoch theoretisch gebrochen: die Entzifferung ist unter Umständen mit geringerem (aber noch immer unrealistisch hohem) Aufwand möglich als das systematische Durchprobieren aller möglicher Schlüssel. AES-192 und AES-256 sind in den USA für staatliche Dokumente mit höchstem Geheimhaltungsgrad zugelassen.[3]

Entstehung

Bis zum Einsatz von AES war der Data Encryption Standard (DES) der am häufigsten genutzte symmetrische Algorithmus zur Verschlüsselung von Daten. Spätestens seit den 1990er Jahren galt er mit seiner Schlüssellänge von 56 Bit als nicht mehr ausreichend sicher gegen Angriffe mit der Brute-Force-Methode. Ein neuer, besserer Algorithmus musste gefunden werden.

Auswahl eines DES-Nachfolgers

Das amerikanische Handelsministerium schrieb die Suche nach einem Nachfolgealgorithmus am 2. Januar 1997 international aus, federführend für die Auswahl war das US-amerikanische National Institute of Standards and Technology in Gaithersburg, Maryland. Nach einer internationalen Konferenz am 15. April 1997 veröffentlichte es am 12. September 1997 die endgültige Ausschreibung. Die Art der Suche sowie die Auswahlkriterien unterschieden sich damit beträchtlich von der hinter verschlossenen Türen erfolgten DES-Entwicklung. Der Sieger der Ausschreibung, der als Advanced Encryption Standard (AES) festgelegt werden sollte, musste folgende Kriterien erfüllen:

AES muss ein symmetrischer Algorithmus sein, und zwar eine Blockchiffre.
AES muss 128 Bit lange Blöcke verwenden (dies wurde erst während der Ausschreibung festgelegt, zu Beginn der Ausschreibung waren auch Blockgrößen von 192 und 256 Bit verlangt, diese wurden nur als mögliche Erweiterungen beibehalten)
AES muss Schlüssel von 128, 192 und 256 Bit Länge einsetzen können.
AES soll gleichermaßen leicht in Hard- und Software zu implementieren sein.
AES soll in Hardware wie Software eine überdurchschnittliche Leistung haben.
AES soll allen bekannten Methoden der Kryptoanalyse widerstehen können und sich für Implementierungen eignen, die sicher gegen Power- und Timing-Attacken sind.
Speziell für den Einsatz in Smartcards sollen geringe Ressourcen erforderlich sein (Codelänge, Speicherbedarf).
Der Algorithmus muss frei von patentrechtlichen Ansprüchen sein und muss von jedermann unentgeltlich genutzt werden können.

Die Auswahlkriterien wurden in drei Hauptkategorien unterteilt: Sicherheit, Kosten sowie Algorithmus- und Implementierungscharakteristiken. Die Sicherheit war der wichtigste Faktor in der Evaluierung und umfasste die Eigenschaften Widerstandsfähigkeit des Algorithmus gegen Kryptoanalyse, Zufälligkeit des Chiffrats, Stichhaltigkeit der mathematischen Basis sowie die relative Sicherheit im Vergleich zu den anderen Kandidaten.

Kosten, der nächste wichtige Faktor, ist im Sinne des Auswahlverfahrens als Überbegriff zu verstehen: Dieser umfasste Lizenzierungsansprüche sowie rechnerische Effizienz auf verschiedenen Plattformen und Speicherverbrauch. Da eines der wichtigsten Ziele, die das NIST ausgearbeitet hatte, die weltweite Verbreitung auf lizenzfreier Basis war und dass AES von jedermann unentgeltlich genutzt werden kann, wurden öffentliche Kommentare und Anregungen zu Lizenzansprüchen und diesbezügliche potenzielle Konflikte spezifisch gesucht.

Die Anforderung der Geschwindigkeit des Algorithmus auf diversen Plattformen wurde in drei zusätzliche Ziele unterteilt:

Die rechnerische Geschwindigkeit mit 128-Bit-Schlüsseln.
Die rechnerische Geschwindigkeit mit 192-Bit- und 256-Bit-Schlüsseln sowie die rechnerische Geschwindigkeit verschiedener Hardware-Implementierungen. Der Speicherverbrauch und die Grenzen von Software-Implementierungen der Kandidaten waren weitere wichtige Aspekte.
Das dritte Ziel, die Algorithmus- und Implementierungscharakteristiken, beinhalteten die Flexibilität, die Eignung für Soft- und Hardware-Implementierungen und die Einfachheit des Algorithmus.

Unter Flexibilität verstand man die Eigenschaften, dass AES die Schlüssel- und Blockgröße über dem Minimum unterstützen musste und dass er in verschiedenen Typen von Umgebungen sowie zusätzlich als Stromchiffre und kryptologische Hashfunktion sicher und effizient zu implementieren war.

Die Ausschreibung führte bis zum Abgabeschluss am 15. Juni 1998 zu fünfzehn Vorschlägen aus aller Welt. Diese wurden in der AES-Konferenz vom 20. bis 22. August 1998 in Ventura (Kalifornien) vorgestellt, öffentlich diskutiert und auf die Erfüllung der genannten Kriterien geprüft. Die AES-Konferenz vom 22. und 23. April 1999 in Rom führte zu einer ersten Diskussion der Ergebnisse und Empfehlungen, welche der fünfzehn Algorithmen weiter betrachtet werden sollten. Die fünf besten Kandidaten (MARS, RC6, Rijndael, Serpent, Twofish) kamen in die nächste Runde.

Alle fünf Kandidaten erfüllen die oben genannten Forderungen, daher wurden weitere Kriterien hinzugezogen. Es folgte eine Überprüfung der Algorithmen auf theoretische Schwachstellen, durch die der Algorithmus möglicherweise zu einem späteren Zeitpunkt durch technischen Fortschritt unsicher werden kann. So konnten zum damaligen Stand technisch nicht realisierbare Vorgehensweisen in einigen Jahren anwendbar sein, ein solches Risiko sollte minimiert werden. Die Staffelung der Kandidaten nach Ressourcenverbrauch und Leistung war eindeutiger. Der Rijndael-Algorithmus hatte sich in Hardware- und Software-Implementierung als überdurchschnittlich schnell herausgestellt. Die anderen Kandidaten haben jeweils in unterschiedlichen Bereichen kleinere Schwächen.

Im Mai des Jahres 2000 wurden die Analysen und öffentlichen Diskussionen abgeschlossen und am 2. Oktober 2000 der Sieger schließlich bekannt gegeben: der belgische Algorithmus Rijndael. Rijndael überzeugte durch seine Einfachheit (die Referenz-Implementierung umfasst weniger als 500 Zeilen C-Code), Sicherheit und Geschwindigkeit, weshalb sich die USA trotz Sicherheitsbedenken für einen europäischen Algorithmus entschieden.

Der Auswahlprozess faszinierte weltweit viele Kryptographen insbesondere durch seine offene Gestaltung. Bis heute wird dieser Wettbewerb als vorbildlich angesehen.

Arbeitsweise

Rijndael ist eine als Substitutions-Permutations-Netzwerk entworfene Blockchiffre. Bei Rijndael können Blocklänge und Schlüssellänge unabhängig voneinander die Werte 128, 160, 192, 224 oder 256 Bits erhalten, während bei AES die Blockgröße auf 128 Bit festgelegt ist und die Schlüsselgröße 128, 192 oder 256 Bit betragen kann.

Rijndael ist eine iterierte Blockchiffre, d. h. der Block wird in mehreren aufeinanderfolgenden Runden verschlüsselt, die bis auf die verwendeten Rundenschlüssel gleich sind. Für jede Runde wird ein anderer Rundenschlüssel aus dem Originalschlüssel berechnet (Schlüsselexpansion). Die Anzahl $R$ der Runden variiert und ist vom Maximum der Blockgröße $b$ und der Schlüssellänge $k$ abhängig (beim AES also nur von der Schlüssellänge):

Anzahl der Runden bei Rijndael
max(b, k)	128	160	192	224	256
Rundenzahl R	10	11	12	13	14

Der Datenblock, der ver- oder entschlüsselt werden soll, wird zunächst in eine zweidimensionale Tabelle geschrieben, deren Zellen ein Byte groß sind und die vier Zeilen und je nach Blockgröße 4 bis 8 Spalten hat.

Ablauf

Schlüsselexpansion
AddRoundKey(Rundenschlüssel[0])
Verschlüsselungsrunden r = 1 bis R-1:
- SubBytes()
- ShiftRows()
- MixColumns()
- AddRoundKey(Rundenschlüssel[r])
Schlussrunde:
- SubBytes()
- ShiftRows()
- AddRoundKey(Rundenschlüssel[R])

S-Box

Rijndael verwendet eine S-Box, um bei der Operation SubBytes() jedes Byte des Datenblocks durch ein anderes zu ersetzen, und sie wird auch bei der Schlüsselexpansion eingesetzt. Eine S-Box (Substitutionsbox) dient zur monoalphabetischen Verschlüsselung. Sie bewirkt vor allem die Verwischung der Beziehung zwischen Klar- und Geheimtext, was in der kryptologischen Fachsprache Konfusion genannt wird, kann aber auch zur Umsetzung des Shannon’schen Prinzips der Diffusion beitragen.

Die S-Box von Rijndael ist nach Kriterien konstruiert, die die Anfälligkeit für die Methoden der linearen und der differentiellen Kryptoanalyse sowie für algebraische Attacken minimieren sollen. Sie besteht aus 256 Bytes, die erzeugt werden, indem jedes Byte außer der Null, aufgefasst als Vertreter des endlichen Körpers $\mathbb {F} _{2^{8}}$ , durch sein multiplikatives Inverses ersetzt wird, worauf noch eine affine Transformation erfolgt.[4] Es ist

S(x)={\overline {x}}\oplus ({\overline {x}}\lll 1)\oplus ({\overline {x}}\lll 2)\oplus ({\overline {x}}\lll 3)\oplus ({\overline {x}}\lll 4)\oplus (63)_{\text{hex}}

.

Dabei steht ${\overline {x}}$ für das multiplikative Inverse von $x$ in $\mathbb {F} _{2^{8}}$ , oder für 0, falls $x=0$ . $b\lll n$ bezeichnet die Linksrotation des Bytes $b$ um $n$ Bitpositionen und $\oplus$ das bitweise XOR.

Die Werte der S-Box und der zum Entschlüsseln benötigten inversen S-Box können entweder für jedes substituierte Byte erneut (dynamisch) berechnet werden, um Speicher zu sparen, oder vorberechnet und in einem Array gespeichert werden.

Schlüsselexpansion

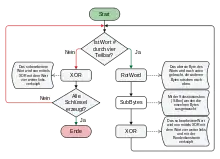
Prinzip der Schlüsselexpansion bei AES

Zunächst müssen aus dem Schlüssel $R+1$ Teilschlüssel (auch Rundenschlüssel genannt) erzeugt werden, die jeweils die gleiche Größe wie ein Datenblock haben. Somit muss der Benutzerschlüssel auf die Länge $b\cdot (R+1)$ expandiert werden, wobei $b$ die Blockgröße in Bit angibt. Der Schlüssel wird in eine zweidimensionale Tabelle mit vier Zeilen und Zellen der Größe 1 Byte abgebildet. Fasst man jede Spalte als 32-bit-Wort auf, ergibt das ein eindimensionales Array mit $b/32\cdot (R+1)$ Elementen.

Sei $N=k/32$ die Länge des Benutzerschlüssels in Wörtern. Dieser wird zunächst in die ersten Wörter $W_{0},\cdots ,W_{N-1}$ des Arrays eingetragen. Dann werden in einer Iteration die weiteren Wörter $W_{i}$ jeweils durch bitweises XOR von $W_{i-1}$ und $W_{i-N}$ berechnet. Für jedes $N$ -te Wort wird $W_{i-1}$ zuvor rotiert, byteweise substituiert und mit einer von $i$ abhängigen Konstanten verknüpft. Falls $N>6$ ist, wird dazwischen alle $N$ Wörter noch eine weitere Substitution ausgeführt.

Für $i=N,\ldots ,b/32\cdot (R+1)-1$ :

W_{i}={\begin{cases}W_{i-N}\oplus \operatorname {S} (W_{i-1}\lll 8)\oplus C_{i/N-1}&{\text{wenn }}i\equiv 0{\pmod {N}}\\W_{i-N}\oplus \operatorname {S} (W_{i-1})&{\text{wenn }}N>6{\text{ und }}i\equiv 4{\pmod {N}}\\W_{i-N}\oplus W_{i-1}&{\text{sonst}}\\\end{cases}}

$\operatorname {S} (x)$ bezeichnet die Substitution jedes Bytes in $x$ durch die gleiche S-Box, die auch beim Verschlüsseln eines Datenblocks eingesetzt wird. $x\lll 8$ ist die Rotation von $x$ um 8 Bitpositionen nach links. Die Konstanten $C_{j}$ werden gebildet, indem $2^{j}$ , berechnet im Körper $\mathbb {F} _{2^{8}}$ , in das höchste Byte von $C_{j}$ eingetragen wird, während die übrigen Bytes 0 sind.

AddRoundKey

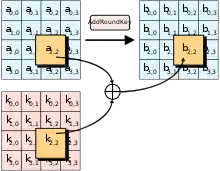
Bitweise XOR-Verknüpfung zwischen dem Block und dem aktuellen Rundenschlüssel

Vor der ersten und nach jeder Verschlüsselungsrunde wird der Datenblock mit einem der Rundenschlüssel XOR-verknüpft. Dies ist die einzige Funktion in AES, in die der Benutzerschlüssel eingeht.

SubBytes

Im ersten Schritt jeder Runde wird jedes Byte $B$ im Block durch den Eintrag $S(B)$ der S-Box ersetzt. Somit werden die Daten byteweise monoalphabetisch verschlüsselt.

ShiftRows

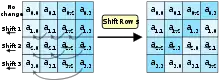
Zeilen werden um eine bestimmte Anzahl von Spalten nach links verschoben

Wie oben erwähnt, liegt ein Block in Form einer zweidimensionalen Tabelle mit vier Zeilen vor. In diesem zweiten Schritt jeder Runde werden die Zeilen um eine bestimmte Anzahl von Spalten nach links verschoben. Überlaufende Zellen werden von rechts fortgesetzt. Die Anzahl der Verschiebungen ist zeilen- und blocklängenabhängig:

r	b=128	b=160	b=192	b=224	b=256
Zeile 1	0	0	0	0	0
Zeile 2	1	1	1	1	1
Zeile 3	2	2	2	2	3
Zeile 4	3	3	3	4	4

Je nach Blocklänge b und Zeile in der Datentabelle wird die Zeile um 1 bis 4 Spalten verschoben.
Für den AES sind nur die fett markierten Werte relevant.

MixColumns

Die Spalten werden vermischt

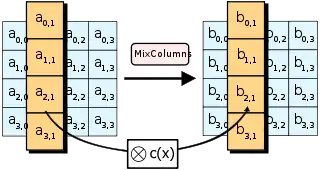
Als dritte Operation jeder Runde außer der Schlussrunde werden die Daten innerhalb der Spalten vermischt. Zur Berechnung eines Bytes $b_{j}$ der neuen Spalte wird jedes Byte $a_{j}$ der alten mit einer Konstanten (1, 2 oder 3) multipliziert. Dies geschieht modulo des irreduziblen Polynoms $x^{8}+x^{4}+x^{3}+x+1$ im Galois-Körper $GF(2^{8})$ . Dann werden die Ergebnisse XOR-verknüpft:

b_{0}=(a_{0}\cdot 2)\oplus (a_{1}\cdot 3)\oplus (a_{2}\cdot 1)\oplus (a_{3}\cdot 1)

b_{1}=(a_{0}\cdot 1)\oplus (a_{1}\cdot 2)\oplus (a_{2}\cdot 3)\oplus (a_{3}\cdot 1)

b_{2}=(a_{0}\cdot 1)\oplus (a_{1}\cdot 1)\oplus (a_{2}\cdot 2)\oplus (a_{3}\cdot 3)

b_{3}=(a_{0}\cdot 3)\oplus (a_{1}\cdot 1)\oplus (a_{2}\cdot 1)\oplus (a_{3}\cdot 2)

In Matrixschreibweise:

{\begin{pmatrix}b_{0}\\b_{1}\\b_{2}\\b_{3}\end{pmatrix}}={\begin{pmatrix}2&3&1&1\\1&2&3&1\\1&1&2&3\\3&1&1&2\end{pmatrix}}{\begin{pmatrix}a_{0}\\a_{1}\\a_{2}\\a_{3}\end{pmatrix}}

Nach den Rechengesetzen in diesem Galois-Körper gilt für die Multiplikation:

$a\cdot 1=a$
$a\cdot 2={\begin{cases}2a&{\text{wenn }}a<2^{7}\\2a\oplus (11{\text{b}})_{\text{hex}}&{\text{wenn }}a\geq 2^{7}\end{cases}}$
$a\cdot 3=(a\cdot 2)\oplus a$

Dabei bezeichnet $2a$ die normale Multiplikation von a mit 2 und $\oplus$ die bitweise XOR-Verknüpfung.

Entschlüsselung

Bei der Entschlüsselung von Daten wird genau rückwärts vorgegangen. Die Daten werden zunächst wieder in zweidimensionale Tabellen gelesen und die Rundenschlüssel generiert. Allerdings wird nun mit der Schlussrunde angefangen und alle Funktionen in jeder Runde in der umgekehrten Reihenfolge aufgerufen. Durch die vielen XOR-Verknüpfungen unterscheiden sich die meisten Funktionen zum Entschlüsseln nicht von denen zum Verschlüsseln. Jedoch muss eine andere S-Box genutzt werden (die sich aus der originalen S-Box berechnen lässt) und die Zeilenverschiebungen erfolgen in die andere Richtung.

Anwendung

AES wird u. a. vom Verschlüsselungsstandard IEEE 802.11i für Wireless LAN und seinem Wi-Fi-Äquivalent WPA2, bei IEEE802.16 m (WiMAX), sowie bei SSH und bei IPsec genutzt. Auch in der IP-Telefonie kommt AES sowohl in offenen Protokollen wie SRTP als auch proprietären Systemen wie Skype[5] zum Einsatz. Mac OS X benutzt AES als Standardverschlüsselungsmethode für Disk-Images, außerdem verwendet der Dienst FileVault AES. Ebenso verwendet die transparente Verschlüsselung EFS in Windows XP ab SP 1 diese Methode. Zudem wird der Algorithmus zur Verschlüsselung diverser komprimierter Dateiarchive verwendet, z. B. bei 7-Zip und RAR. In PGP und GnuPG findet AES ebenfalls einen großen Anwendungsbereich. Der Linear Tape Open Standard spezifiziert eine Schnittstelle für AES-Verschlüsselung durch das Bandlaufwerk ab LTO-4 und ermöglicht so Bandkompression bei gleichzeitiger Verschlüsselung.

AES gehört zu den vom Projekt NESSIE empfohlenen kryptografischen Algorithmen und ist Teil der Suite B der NSA.

Der AES-Algorithmus wird inzwischen in etlichen CPUs von Intel oder AMD durch zusätzliche spezialisierte Maschinenbefehle unterstützt, wodurch das Verschlüsseln 5-mal und das Entschlüsseln 25-mal schneller als mit nicht spezialisierten Maschinenbefehlen erfolgt.[6] Damit ist AES auch für mobile Anwendungen Akku-schonend benutzbar und für den Masseneinsatz geeignet. Programmier-Softwarebibliotheken wie zum Beispiel OpenSSL erkennen und nutzen die Hardware-AES-Implementierung und greifen nur wenn nötig auf langsamere Softwareimplementierung zurück.

AES-verschlüsselte Kommunikation wird auch zur Verschlüsselung der Datenübertragung zwischen elektronischen Identitätsdokumenten und Inspektionsgeräten verwendet, zum Beispiel bei neueren Reisepässen oder dem Deutschen Personalausweis. So wird das Abhören dieser Kommunikation verhindert. Hier erfolgt die Berechnung meist in dedizierten Koprozessoren für DES und AES, sowohl erheblich schneller als auch sicherer als in einer Allzweck-CPU möglich.

Da AES eine Blockverschlüsselung ist, sollte ein Betriebsmodus verwendet werden um die Blöcke zu verketten. Dadurch wird die Sicherheit weiter erhöht.

Schwächen und Angriffe

Kritikpunkte

Rijndael überzeugte im AES-Wettbewerb durch seine mathematisch elegante und einfache Struktur sowie durch seine Effizienz. Allerdings sahen manche Kryptographen gerade darin ein Problem:

Die S-Boxen lassen sich algebraisch einfach beschreiben, und sie sind die einzige nichtlineare Komponente der Chiffre. Dadurch lässt sich der gesamte Algorithmus als Gleichungssystem beschreiben.[7]
Durch die einfache Schlüsseleinteilung würden mit einem beliebigen Rundenschlüssel auch 128 Bit des Verfahrensschlüssels kompromittiert.

Ein weiterer Kritikpunkt war die relativ geringe Sicherheitsmarge, die nach damaligem Stand der Analyse nur drei (bei 128 Bit Schlüssellänge) bis fünf Runden (bei 256 Bit Schlüssellänge) betrug.[7]

Biclique-Angriff

Auf der Rump-Session der Konferenz CRYPTO im August 2011 stellten die Kryptologen Andrey Bogdanov, Dmitry Khovratovich und Christian Rechberger den ersten Angriff auf den vollen AES-Algorithmus vor.[2] Dieser Angriff ist bei den verschiedenen Schlüssellängen im Schnitt etwa um den Faktor 4 schneller als ein vollständiges Durchsuchen des Schlüsselraumes. Damit zeigt er die prinzipielle Angreifbarkeit von AES, ist aber für die praktische Sicherheit nicht relevant. Der Angriff berechnet den geheimen Schlüssel von AES-128 in 2^126,1 Schritten. Bei AES-192 werden 2^189,7 Schritte, bei AES-256 2^254,4 Schritte benötigt.

XSL-Angriff

2002 wurde von Courtois und Pieprzyk ein theoretischer Angriff namens XSL (für eXtended Sparse Linearization) gegen Serpent und Rijndael vorgestellt (siehe Serpent). Mit dem XSL-Angriff ist nach Angabe der Autoren eine Komplexität im Bereich von $2^{100}$ Operationen erreichbar. XSL ist die Weiterentwicklung einer heuristischen Technik namens XL (für eXtended Linearization), mit der es manchmal gelingt, große nichtlineare Gleichungssysteme effizient zu lösen. XL wurde ursprünglich zur Analyse von Public-Key-Verfahren entwickelt. Der Einsatz im Kontext von symmetrischen Kryptosystemen ist eine Innovation von Courtois und Pieprzyk. Grob kann die Technik und ihre Anwendung auf symmetrische Kryptosysteme wie folgt beschrieben werden:

Die Blockchiffre wird als überspezifiziertes System quadratischer Gleichungen in GF(2) beschrieben. Überspezifiziert bedeutet, dass es mehr Gleichungen als Variablen gibt. Variablen und Konstanten können nur die Werte 0 und 1 annehmen. Die Addition entspricht dem logischen eXklusiv-OdeR (XOR), die Multiplikation dem logischen UND. Eine solche Gleichung könnte wie folgt aussehen:

x_{1}+x_{2}\cdot x_{3}+x_{2}\cdot x_{4}\equiv 1\mod 2

Diese Gleichung besteht aus einem linearen Term (der Variablen $x_{1}$ ), zwei quadratischen Termen ( $x_{2}\cdot x_{3}$ und $x_{2}\cdot x_{4}$ ) und einem konstanten Term ( $1$ ).

Einige Wissenschaftler zweifeln die Korrektheit der Abschätzungen von Courtois und Pieprzyk an:

“I believe that the Courtois-Pieprzyk work is flawed. They overcount the number of linearly independent equations. The result is that they do not in fact have enough linear equations to solve the system, and the method does not break Rijndael … The method has some merit, and is worth investigating, but it does not break Rijndael as it stands.”

„Ich glaube, dass die Arbeit von Courtois und Pieprzyk fehlerhaft ist; sie schätzen die Anzahl der linear unabhängigen Gleichungen zu hoch ein. Das Resultat ist, dass sie in Wirklichkeit nicht genug lineare Gleichungen erhalten, um das System zu lösen, und die Methode somit Rijndael nicht bricht […] Die Methode besitzt ihre Vorzüge und ist es wert, weiter untersucht zu werden, allerdings bricht sie in ihrer aktuellen Form Rijndael nicht.“

– Don Coppersmith[8]

Diese Art von System kann typischerweise sehr groß werden, im Falle der 128-Bit-AES-Variante wächst es auf 8000 quadratische Gleichungen mit 1600 Variablen an, womit der XSL-Angriff in der Praxis nicht anwendbar ist. Das Lösen von Systemen quadratischer Gleichungen ist ein NP-schweres Problem mit verschiedenen Anwendungsfeldern in der Kryptographie.

Weitere Angriffe

Kurz vor der Bekanntgabe des AES-Wettbewerbs stellten verschiedene Autoren eine einfache algebraische Darstellung von AES als Kettenbruch vor. Dies könnte für erfolgreiche Angriffe genutzt werden. Hierzu gibt es einen Videovortrag von Niels Ferguson auf der HAL 2001.[9]

Im Jahr 2003 entdeckten Sean Murphy und Matt Robshaw eine alternative Beschreibung des AES, indem sie diesen in eine Blockchiffre namens BES einbetteten, welche anstatt auf Datenbits auf Datenblöcken von 128 Bytes arbeitet. Die Anwendung des XSL-Algorithmus auf BES reduziert dessen Komplexität auf 2¹⁰⁰, wenn die Kryptoanalyse von Courtois und Pieprzyk korrekt ist.

Im Mai 2005 veröffentlichte Daniel Bernstein einen Artikel über eine unerwartet einfache Timing-Attacke[10] (eine Art der Seitenkanalattacke) auf den Advanced Encryption Standard.

Die Forscher Alex Biryukov und Dmitry Khovratovich veröffentlichten Mitte des Jahres 2009 einen Angriff mit verwandtem Schlüssel[11] auf die AES-Varianten mit 192 und 256 Bit Schlüssellänge. Dabei nutzten sie Schwächen in der Schlüsselexpansion aus und konnten eine Komplexität von 2¹¹⁹ erreichen. Damit ist die AES-Variante mit 256 Bit Schlüssellänge formal schwächer als die Variante mit 128 Bit Schlüssellänge.[12] Ende 2009 wurde mit einer Verbesserung des Angriffs eine Komplexität von nur noch 2^99,5 erreicht.[13] Für die Praxis hat dieser Angriff jedoch wenig Relevanz, denn AES bleibt weiterhin praktisch berechnungssicher.[13]

Im März 2012 wurde bekannt, dass die NSA in ihrem neuen Utah Data Center neben dem Speichern großer Teile der gesamten Internetkommunikation auch mit enormen Rechenressourcen am Brechen von AES arbeitet.[14] Die Eröffnung des Rechenzentrums läuft schrittweise seit September 2013.[15]

Craig Ramsay & Jasper Lohuis, als Forscherteam der beiden Unternehmen Fox-IT und Riscure, beschreiben 2017[16] einen Angriff, bei dem sie die von der CPU abgestrahlten Funksignale zur Entschlüsselung verwenden. Damit ließe sich der AES-Schlüssel in maximal fünf Minuten ermitteln, wenn Sniffer und angegriffene CPU etwa 1 Meter entfernt voneinander stehen. Bei 30 Zentimeter Distanz schrumpfe die Zeit auf etwa 50 Sekunden.[17] Man muss aber beachten, dass dies ein Angriff auf eine einzelne Implementierung des Algorithmus auf einer bestimmten CPU ist, nicht auf den Algorithmus an sich. Ein solcher Angriff ist nur unter sehr speziellen Bedingungen durchführbar und kann nicht unbedingt verallgemeinert werden.

Literatur

Joan Daemen, Vincent Rijmen: The Design of Rijndael. AES: The Advanced Encryption Standard. Springer, Berlin u. a. 2002, ISBN 3-540-42580-2 (Information Security and Cryptography), (englisch).

Weblinks

Offizielle Spezifikation des AES vom NIST, doi:10.6028/NIST.FIPS.197
Angriffe auf die Sicherheit von AES
Beschreibung von Markus Repges der AES-Kandidaten (Finalisten)
NIST, Report on the Development of the Advanced Encryption Standard (AES), 2. Oktober 2000 (PDF; 383 kB)
Animation von AES in Englisch – AES mit Flash erklärt und animiert (Flash-Animation by Enrique Zabala / Universität ORT / Montevideo / Uruguay). Verfügbar auch in Deutsch als ZIP-Datei. Diese Animation ist (in deutsch, englisch und spanisch) auch Teil von CrypTool 1, Menü Einzelverfahren -> Visualisierung von Algorithmen -> AES.
AESPipe – Komfortable Ver-/Entschlüsselung von Datenströmen für die Linuxshell (StdIn nach StdOut)
AES Artikel – Sehr detaillierte deutsche Erklärung des AES mitsamt Rechenbeispielen und Implementierung in der Programmiersprache C
Applied Crypto++: Block Ciphers Ein Artikel über Crypto++ auf codeproject.com mit dem Titel Encrypt Data using Symmetric Encryption with Crypto++

Einzelnachweise

Im Rijndael-Algorithmus werden Blockgrößen von 128, 160, 192, 224, und 256 Bits unterstützt, im AES-Standard wird aber nur eine 128-bit Blockgröße spezifiziert.
Andrey Bogdanov, Dmitry Khovratovich, Christian Rechberger: Biclique Cryptanalysis of the Full AES. In: ASIACRYPT 2011 (= Lecture Notes in Computer Science). Band 7073. Springer, 2011, S. 344–371 (microsoft.com [PDF; abgerufen am 29. November 2012]). Biclique Cryptanalysis of the Full AES (Memento vom 6. März 2016 im Internet Archive)
Committee on National Security Systems: CNSS Policy No. 15, Fact Sheet No. 1. 2003, S. 2 (nist.gov [PDF]).
Beschreibung des AES von Sam Trenholme (englisch)
Tom Berson: Skype Security Evaluation (Memento vom 25. Oktober 2005 im Internet Archive) auf skype.com mit Signatur, 18. Oktober 2005, englisch, PDF
Oliver Lau (2013): „Spezialkommando. Schnelle AES-Chiffres mit Intrinsics“ in: c’t 2013, Heft 14, Seiten 174–177. Zitierte Aussage siehe Seite 176 und 177.
Niels Ferguson, Bruce Schneier: Practical Cryptography. Wiley Publishing, Indianapolis 2003, ISBN 978-0-471-22357-3, S. 56.
Comments from Readers
ftp.ccc.de
Cache-timing attacks on AES (PDF-Version; 426 kB)
Related-key Cryptanalysis of the Full AES-192 and AES-256 (PDF; 354 kB)
FAQ zum Angriff (Memento vom 13. November 2013 im Internet Archive)
Biryukov, Alex; Khovratovich, Dmitry: „Related-key Cryptanalysis of the Full AES-192 and AES-256“, (4. Dezember 2009)
The NSA Is Building the Country’s Biggest Spy Center (Watch What You Say)
Bericht: Größtes NSA-Rechenzentrum läuft sich warm
fox-it.com
Dusan Zivadinovic: AES-Schlüssel stehlen: Van-Eck-Phreaking für 200 Euro. Abgerufen am 18. September 2017.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[blocksize-1] Im Rijndael-Algorithmus werden Blockgrößen von 128, 160, 192, 224, und 256 Bits unterstützt, im AES-Standard wird aber nur eine 128-bit Blockgröße spezifiziert.

[biclique-2] Andrey Bogdanov, Dmitry Khovratovich, Christian Rechberger: Biclique Cryptanalysis of the Full AES. In: ASIACRYPT 2011 (= Lecture Notes in Computer Science). Band 7073. Springer, 2011, S. 344–371 (microsoft.com [PDF; abgerufen am 29. November 2012]). Biclique Cryptanalysis of the Full AES (Memento vom 6. März 2016 im Internet Archive)

[3] Committee on National Security Systems: CNSS Policy No. 15, Fact Sheet No. 1. 2003, S. 2 (nist.gov [PDF]).

[4] Beschreibung des AES von Sam Trenholme (englisch)

[5] Tom Berson: Skype Security Evaluation (Memento vom 25. Oktober 2005 im Internet Archive) auf skype.com mit Signatur, 18. Oktober 2005, englisch, PDF

[6] Oliver Lau (2013): „Spezialkommando. Schnelle AES-Chiffres mit Intrinsics“ in: c’t 2013, Heft 14, Seiten 174–177. Zitierte Aussage siehe Seite 176 und 177.

[ferguson-7] Niels Ferguson, Bruce Schneier: Practical Cryptography. Wiley Publishing, Indianapolis 2003, ISBN 978-0-471-22357-3, S. 56.

[8] Comments from Readers

[9] tp.ccc.de

[10] Cache-timing attacks on AES (PDF-Version; 426 kB)

[11] Related-key Cryptanalysis of the Full AES-192 and AES-256 (PDF; 354 kB)

[12] FAQ zum Angriff (Memento vom 13. November 2013 im Internet Archive)

[BK09-13] Biryukov, Alex; Khovratovich, Dmitry: „Related-key Cryptanalysis of the Full AES-192 and AES-256“, (4. Dezember 2009)

[14] The NSA Is Building the Country’s Biggest Spy Center (Watch What You Say)

[15] Bericht: Größtes NSA-Rechenzentrum läuft sich warm

[16] x-it.com

[17] Dusan Zivadinovic: AES-Schlüssel stehlen: Van-Eck-Phreaking für 200 Euro. Abgerufen am 18. September 2017.