Mathematica
Mathematica ist eines der meistbenutzten mathematisch-naturwissenschaftlichen Programmpakete und ein proprietäres Softwarepaket des Unternehmens Wolfram Research. Mathematica 1.0 wurde 1988 auf den Markt gebracht.
| Wolfram Mathematica | |
|---|---|

| |
 | |
| Basisdaten | |
| Entwickler | Wolfram Research |
| Erscheinungsjahr | 23. Juni 1988 |
| Aktuelle Version | 13.0[1] (13. Dezember 2021) |
| Betriebssystem | Microsoft Windows[2], Linux[2], macOS[2] |
| Programmiersprache | C, C++[3], Java[3], Wolfram Language |
| Kategorie | Computeralgebrasystem, Informationsvisualisierung, Statistik-Software, Grafische Benutzeroberfläche |
| Lizenz | Proprietäre Software |
| wolfram.com/products/mathematica | |
Programmpaket Mathematica
Das Softwarepaket „Mathematica“ enthält unter anderem
- ein Computeralgebrasystem zur symbolischen Verarbeitung von Gleichungen und Differentialgleichungen.[4][5]
- eine Numerik-Software zum numerischen Lösen oder Auswerten von Gleichungen
- ein Visualisierungs-Tool zum Darstellen von Graphen und 3D/2D Graphiken
- eine Programmiersprache, die Elemente des prozeduralen, objektorientierten, funktionalen und regelbasierten Programmierens in sich vereint.
Der Autor und Unternehmensbegründer Stephen Wolfram begann die Entwicklungsarbeit im Jahr 1986, die erste Version von Mathematica wurde 1988 herausgebracht. Der Name Mathematica wurde Wolfram zufolge von Steve Jobs vorgeschlagen.[6][7]
Benutzung und Arbeitsmethode
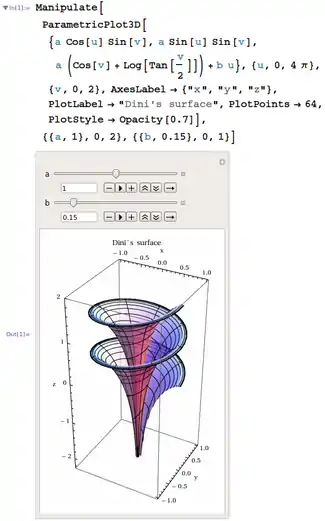
Mathematica besteht aus dem Kernel, der die Berechnungen vornimmt, sowie dem Notebook, einer grafische Benutzeroberfläche. Das Programms wird in der Regel über das Notebook bedient, das die Ein- und Ausgabe formatiert darstellt. Das Notebook hat außerdem Funktionen einer Textverarbeitung und erlaubt das Darstellen und Manipulieren von Grafiken. Ein besonderes Merkmal ist auch die umfangreiche Unterstützung mathematischer Sonderzeichen, die in Mathematica (im Gegensatz zu klassischen Programmiersprachen) an jeder Stelle (auch als Variablennamen) genutzt werden können.
Der Kernel verarbeitet den Programmcode in der Regel gleich nach der Eingabe (als Interpreter), Ergebnisse oder Programmierfehler sind damit sofort zu sehen, das Programmieren ist interaktiv. Wird Programmcode mehrfach durchlaufen, etwa beim nicht-interaktiven Programmaufruf, so wird der Programmcode automatisch kompiliert. Der Programmcode ist betriebssystemunabhängig. Mathematica wird angeboten für Windows, Linux und macOS, bis einschließlich Version 6.0.3 auch für MS-DOS, NeXT, OS/2, Unix und VMS.
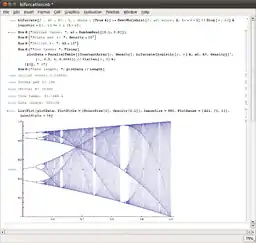
Ab Version 8 ist der sogenannte free form input in Mathematica verfügbar, der es ermöglicht, anstatt der Eingabe der korrekten Syntax für Berechnungen und andere Befehle, „natürliches“ Englisch zu verwenden. Dafür ist allerdings eine Internetverbindung nötig. So wird beispielsweise das gleiche Ergebnis – der Graph der Sinusfunktion mit hellroter Füllung und gestrichelten Linien – erzielt, wenn man
Show[
Plot[Sin[x], {x, -6.6, 6.6},
Filling -> Axis,
FillingStyle -> Lighter[Red]
],
GridLines -> Automatic,
GridLinesStyle -> Dashed
]
eingibt, wie aber auch den free form input verwendend
plot sin x with light red filling and dashed grid lines
als Befehl nimmt. Nachdem man einen mit free form input vorgenommenen Befehl getätigt hat, kann man ihn in die genaue Syntax übersetzen lassen und dann wieder verändern, sodass Kenntnis über die Syntax dennoch von Vorteil bleibt.[8][9]
Mathematica wird in der Wissenschaft beziehungsweise im Studium natur- oder wirtschaftswissenschaftlicher Fächer eingesetzt. Ebenso wendet es sich an den professionellen Anwender in der Industrie und Wirtschaft. So verwenden Banken Mathematica zur Simulation von Aktienkursentwicklung, Bewertung von Derivaten, Risikoabschätzung und -wandlung und so weiter. Die Anforderung an die Korrektheit der Ergebnisse (analytisch wie numerisch) ist daher hoch.
Neben den Grundrechenarten, Ableitungs- und Integralberechnung, Lösen von Gleichungssystemen, Matrizenmanipulation und numerischen Berechnungen in beliebiger Genauigkeit (keine Beschränkung auf die Maschinenpräzision) sind eine Vielzahl spezieller Funktionen, etwa aus den Bereichen der Kombinatorik, implementiert. Die Programmiersprache von Mathematica umfasst implizite Typenzuweisung und -wandlung, automatisches Speichermanagement und Musterauswertungstechniken (englisch pattern matching). Seit Ende 2013 wird die Programmiersprache Wolfram Language unabhängig von Mathematica vertrieben[10].
Sprache
Die Programmiersprache von Mathematica (Wolfram Language[11]) ist stark an die funktionale Programmiersprache Lisp angelehnt. Zusätzlich basiert Mathematica wesentlich auf Pattern Matching (wie zum Beispiel auch Haskell). Dies sorgt besonders bei Einsteigern für Verwirrung, weil Patterns, also Muster-Platzhalter, vorkommen, sobald man mit Funktionen arbeitet. Zusammen mit den fast ständig genutzten eckigen Klammern entsteht so ein Code-Aussehen, das sich stark von den verbreiteten C-artigen Programmiersprachen unterscheidet. Bei folgender Definition handelt es sich für Mathematica nicht um eine Funktion, sondern um eine Ersetzungsregel, bei der jedes Vorkommen von f[irgendwas] durch irgendwas + irgendwas ersetzt wird, wobei irgendwas sprichwörtlich alles sein kann:
f[x_] = x + x
Eine wirkliche Funktion im Sinne der funktionalen Programmierung/des Lambda-Kalküls wird hingegen durch Function erzeugt:
f = Function[x, x + x]
Der Vorteil des Pattern-Matching in der Computeralgebra liegt darin, dass man komplizierte Ersetzungsregeln kompakt schreiben kann. Eine abschnittsweise definierte Funktion könnte man über Matching-Regeln wie folgt definieren:
g[x_ /; x < 7] = 2*x; g[x_ /; x > 7] = 3*x;
Aufrufe g[3] werden damit als 2*3=6 ausgewertet, wohingegen g[10] die Auswertung 3*10=30 ergibt.
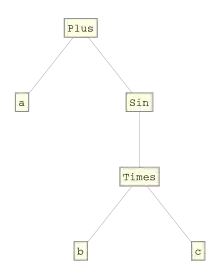
Plus[a,Sin[Times[b,c]]] als TreeFormWie Lisp weist Mathematica die Eigenschaft der Homoikonizität auf. Das bedeutet, dass Mathematica-Code und das Ergebnis einer Berechnung aus demselben Typ Daten besteht. Mathematica-Anweisungen wie -Ausgaben sind eigentlich Bäume, und eine Auswertung einer Eingabe besteht in der Transformation eines solchen Baumes. Aus diesem Grund nennt man das erste Element eines Mathematica-Ausdruckes auch Head, im folgenden Beispiel ist der Head die Anweisung Plus:
Plus[a,Sin[Times[b,c]]]
Als Baum dargestellt sieht dieser Ausdruck wie rechts gezeigt aus. Der Head (also Wurzelknoten) des Baumes ist die Funktion Plus. Mathematica kennt verschiedene Weisen, Ein/Ausgaben darzustellen. In natürlicher Schreibweise entspricht dieser Ausdruck dem besser lesbaren
a + Sin[b*c]
Mathematica unterstützt als Computeralgebrasystem die Verarbeitung beliebiger Symbole in derartigen Ausdrücken. Anhand von einer Liste von Ersetzungsregeln werden diese Ausdrücke zu anderen Bäumen umgeformt. So zusammengebaut sind komplexe Rechnungen möglich. Mathematica ist damit dynamisch typisiert. Im Gegensatz zu anderen Sprachen ist bei Mathematica damit eine nicht auswertbare Zeile im Allgemeinen kein Fehler, sondern verbleibt unverändert als Rückgabe. Fehlerausgaben sind aber dennoch möglich, zum Beispiel bei Übergabe ungeeigneter Argumente an eine (eingebaute) Funktion wie Plot.
Der Programmierer ist nicht auf ein einziges Programmierparadigma festgelegt, sondern kann ebenso imperative Anweisungen programmieren. Durch zehntausende von eingebauten Funktionen kann man sehr schnell umfangreiche Programme schreiben.
Sprachbeispiele
Beispiel 1: Primzahlen
Mehrere Primzahlen werden von der Funktion berechnet
In[1] := Prime /@ Range[5]
Out[1] = {2, 3, 5, 7, 11}
Die Liste der Primzahlen wird blockweise über Primzahlstufen selektiert
In[1] := max = 3; l = {}; s = -1; m = 1; k = 1; For[t = 0, t <= max, t++,
s += 1/(2 t + 1); ns = Denominator[s]; r = (t + s)/2; sk = s k;
m += 8 (t + 1);
For[n = 2 k - 1, n < m, n += 2,
If[Denominator[sk - r] == ns, l = AppendTo[l, n]]; sk += s;
k++]]; l = Rest[l]; l = PrependTo[l, 2]; l
Out[1] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79}
Beispiel 2: Mittelwertberechnung
Untenstehend drei Arten, mit „Mathematica“ den Mittelwert einer Werteliste zu berechnen. Im interaktiven Modus nummeriert Mathematica die Ein- und Ausgaben und liefert die Ergebnisse direkt.
Werteliste definieren:
In[1] := myData = Range[8]
Out[1] = {1, 2, 3, 4, 5, 6, 7, 8}
Mathematica-eigene Funktion benutzen:
In[2] := Mean[myData]
Out[2] = 9/2
Listenmanipulation benutzen:
In[3] := Plus@@myData / Length[myData]
:Out[3] = 9/2
Prozedurales Vorgehen:
In[4] := ''' summe = 0 ''' Out[4] = 0 In[5] := For[ j=1,j <= Length[myData], j++, summe += myData[[j]] ] In[6] := summe / Length[myData] Out[6] = 9/2
Versionsgeschichte
| Version | Veröffentlichung |
|---|---|
| 1.0 | 23. Juni 1988 |
| 1.1 | 31. Oktober 1988 |
| 1.2 | 1. August 1989 |
| 2.0 | 15. Januar 1991 |
| 2.1 | 15. Juni 1992 |
| 2.2 | 1. Juni 1993 |
| 3.0 | 3. September 1996 |
| 4.0 | 19. Mai 1999 |
| 4.1 | 2. November 2000 |
| 4.2 | 1. November 2002 |
| 5.0 | 12. Juni 2003 |
| 5.1 | 25. Oktober 2004 |
| 5.2 | 20. Juni 2005 |
| 6.0 | 1. Mai 2007 |
| 7.0 | 18. November 2008 |
| 7.0.1 | 5. März 2009 |
| 8.0 | 15. November 2010 |
| 8.0.1 | 7. März 2011 |
| 8.0.4 | 24. Oktober 2011 |
| 9.0 | 28. November 2012 |
| 9.0.1 | 30. Januar 2013 |
| 10 | 9. Juli 2014 |
| 10.0.1 | 17. September 2014 |
| 10.0.2 | 15. Dezember 2014 |
| 10.1 | 31. März 2015 |
| 10.2 | 14. Juli 2015 |
| 10.3 | 15. Oktober 2015 |
| 10.3.1 | 16. Dezember 2015 |
| 10.4 | 2. März 2016 |
| 10.4.1 | 18. April 2016 |
| 11 | 9. August 2016 |
| 11.0.1 | 28. September 2016 |
| 11.1 | 16. März 2017 |
| 11.1.1 | 25. April 2017 |
| 11.2 | 14. September 2017 |
| 11.3 | 8. März 2018 |
| 12.0 | 16. April 2019 |
| 12.1 | 18. März 2020 |
| 12.2 | 16. Dezember 2020 |
| 12.3 | 20. Mai 2021 |
| 12.3.1 | Juli 2021 |
| 13.0 | 13. Dezember 2021 |
Probleme
2014 haben drei Mathematiker veröffentlicht, dass Mathematica bei der Berechnung von Determinanten bestimmter Matrizen mit recht großen Ganzzahlen (10.000 Stellen) falsche Ergebnisse liefert. Dieser Fehler sei 2013 gemeldet und auch nach über einem Jahr nicht behoben worden; die Darstellung von Wolfram Research widerspricht diesen Angaben jedoch in Teilen und geht von einem neuen Fehler aus.[12] Der Berechnungsfehler (CASE:303438) ist ab Version 11.1 behoben und nicht mehr vorhanden.
Siehe auch
- Wolfram Alpha
- Liste von Statistik-Software
- Wissenschaftliches Rechnen
- Sage (Software), Open Source Alternative
Literatur
- Hans Benker: MATHEMATICA kompakt: Mathematische Problemlösungen für Ingenieure, Mathematiker und Naturwissenschaftler. Springer, Berlin / Heidelberg 2016, ISBN 978-3-662-49610-7.
- Stephen Wolfram: An Elementary Introduction to the Wolfram Language. Wolfram Media, Inc., Champaign, IL. 2015, ISBN 978-1-944183-00-4.
- Knut Lorenzen: Einführung in Mathematica: Berücksichtigt die kostenlose Version 10 für den Raspberry Pi. mitp Verlags GmbH & Co., 2014. ISBN 978-3-8266-9666-4.
- Axel Kilian: Programmieren mit Wolfram Mathematica. Springer, Berlin / Heidelberg 2009, ISBN 978-3-642-04671-1.
- Michael Trott: The Mathematica GuideBook for Symbolics. Springer, 2006.
- Michael Trott: The Mathematica GuideBook for Programming. Springer, 2004.
- Michael Trott: The Mathematica GuideBook for Numerics. Springer, 2006.
- Michael Trott: The Mathematica GuideBook for Graphics. Springer, 2004.
- Stephen Wolfram: The Mathematica Book. 5. Auflage. Wolfram Media, 2004, ISBN 1-57955-022-3.
- Leonid Shifrin: Mathematica programming. (mathprogramming-intro.org – kostenloses E-Book).
- David B. Wagner: Power Programming With Mathematica: The Kernel. McGraw-Hill Education, 1996, ISBN 0-07-912237-X (dropbox.com [PDF] kostenloses E-Book zu Mathematica).
Weblinks
- Wolfram Research, Inc.
- Offizielle Mathematica-Homepage des deutschen Partners
- Wolfram Alpha (auf Mathematica basierender Internetdienst von Wolfram Research)
- Der Mathematica Integrator
- List of numerical analysis software (englischsprachige Wikipedia)
- Mathematica auf dem Raspberry Pi kostenlose Mathematica-Version für nicht kommerzielle Nutzung
Einzelnachweise
- Launching Version 13.0 of Wolfram Language + Mathematica.
- www.wolfram.com.
- The Software Engineering of Mathematica. 2012 (abgerufen am 7. Januar 2019).
- Barak Katz: Introduction to Mathematica. (PDF; 1.6 MB) 2008, abgerufen am 27. März 2020 (englisch).
- Paritosh Mokhasi: Solving Differential Equations in Mathematica. In: WOLFRAM Computation meets knowledge. Abgerufen am 27. März 2020 (englisch, Webseite mit eingebettem Video).
- Stephen Wolfram: Mathematica. A System for Doing Mathematics by Computer. Addison-Wesley Publishing Company, 1988, ISBN 0-201-19334-5, S. XVIII.
- Stephen Wolfram: Steve Jobs. A Few Memories. In: Stephen Wolfram. Writings. 6. Oktober 2011, abgerufen am 6. März 2020 (englisch).
- wolfram.com (Memento des Originals vom 14. April 2012 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis. Video über den free form input
- wolfram.com free form linguistic input
- Heise, 15. November 2013: Mathematica-Chef Wolfram kündigt Programmiersprache an, Herstellerlink: Wolfram Programming Language
- wolfram.com Wolfram Language – Wissensbasiertes Programmieren
- heise.de