Netztheorie
Die Netztheorie ist eine Entwurfsmethode für Faser-Kunststoff-Verbunde. Sie wurde in den Anfängen der Faserverbundverarbeitung entwickelt. In der Netztheorie wird das Mittragen der Matrix vernachlässigt und die Fasern als selbsttragendes Netz angenommen. Dadurch ist die Netztheorie in der Lage, durch einfache Kräftegleichgewichte die Schichtspannungen zu ermitteln. Da nur Kräftegleichgewichte aufgestellt werden müssen, sind in der Netztheorie keine elastischen Größen notwendig.
Die Netztheorie ist auf Membranspannungszustände beschränkt. Sie kann Laminate mit bis zu vier Faserrichtungen behandeln. Mit der Netztheorie ausgelegte Bauteile sind gewichts- und steifigkeitsoptimal. Dies folgt aus den Kriterien von Michel und Maxwell.
Annahmen und Definitionen
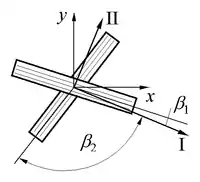
- Nur ebene Spannungszustände (2-axial) sind behandelbar.
- Die Matrix wird vernachlässigt.
- Es treten nur Spannungen parallel zur Faser auf.
- Die Schichten werden aus idealen UD-Schichten aufgebaut.
- Die Schichtwinkel werden in Bezug auf das Koordinatensystem der Hauptnormalspannungen angegeben.
Anwendung
Vorteile
Die Netztheorie findet Anwendung bei Bauteilen, die langzeitig oder bei hohen Temperaturen belastet werden. Da unter diesen Bedingungen die Matrix kriecht bzw. relaxiert, lagern sich die Lasten in die Fasern um. Der Traganteil der Matrix verringert sich, damit wird die Annahme der Netztheorie immer besser erfüllt. Bauteile, die nach Netztheorie ausgelegt sind, sind auch bei Versagen der Matrix weitgehend tragfähig. Daher findet die Netztheorie besonders im Druckbehälter- und Rohrleitungsbau Anwendung.
Schwingend beanspruchte Bauteile, die mit der Netztheorie ausgelegt sind, haben besonders hohe Schwingfestigkeiten. Grund ist die geringe Beanspruchung der Matrix und der Faser-Matrix-Haftflächen.
Die Netztheorie dient als Entwurfsmethode, um leichtbauoptimale Laminate zu finden. Ein solcher Entwurf kann dann mit der klassischen Laminattheorie präzisiert werden. Allgemein stimmen die Ergebnisse nach klassischer Laminattheorie und Netztheorie umso besser überein, je größer das Verhältnis Längs- zu Quermodul der unidirektionalen Schicht ist.
Nachteile
Die Netztheorie ist eine konservative Entwurfsmethode. Die Ausnutzung der Bauteile ist geringer, als beim Entwurf mit der klassischen Laminattheorie. Nach dieser Methode ausgelegte Laminate versagen schlagartig. Da sie statisch bestimmt sind, können sie keine Lasten umlagern. Das Versagen einer Schicht führt zum Totalversagen des Laminats.
Das Ergebnis der Auslegung ist in manchen Fällen nur für einen bestimmten Spannungszustand optimal. Dieser muss vor der Auslegung bekannt sein. Ändert sich die Belastung in Betrag und Richtung, ist das Laminat theoretisch nicht mehr tragfähig. Da die Matrix in der Realität jedoch Lasten überträgt, sind die Laminate dennoch nutzbar. Der Entwurf von robusten Laminaten ist möglich.
Die Netztheorie ist für biegebeanspruchte Bauteile nicht anwendbar. Sie liefert keine globalen Elastizitätskonstanten. Es sind weiterhin keine beliebigen Faseraufbauten berechenbar. Die Netztheorie liefert nur globale Schichtspannungen und nicht die Spannung in Faser und Matrix.
Entwurfsregeln
Die Entwurfsregeln basieren auf den Hauptnormalspannungen. Im Hauptnormalspannungssystem wirken nur Normalspannungen und keine Schubspannungen. Es sind auch Aufbauten tragfähig, die die folgenden Regeln verletzen. Diese Aufbauten sind aber nur mit einem erhöhten Faseraufwand herstellbar.
Regel 1
In allen zugbelasteten Schichten muss die gleiche Zugspannung, in allen druckbelasteten Schichten die gleiche Druckspannung herrschen
Diese Regel spiegelt das Prinzip der gleichmäßigen Ausnutzung wider.
Regel 2
Eine optimale Faseranordnung ist immer dann erreicht, wenn die Fasern in den Hauptnormalspannungs-Richtungen liegen.
Ein Kreuzverbund ist somit immer ein optimales Laminat, da sich bei ihm die Fasern unter 90° kreuzen. Lediglich seine Schichtdicken müssen noch angepasst werden.
Regel 3
Die Hauptnormalspannungen haben gleiche Vorzeichen. Die Faserwinkel müssen so gewählt werden, dass alle Schichtkräfte das gleiche Vorzeichen haben.
Regel 4
Die Hauptnormalspannungen haben unterschiedliche Vorzeichen. Es gibt nur eine optimale Faseranordnung, nämlich in den Hauptspannungsachsen.
Beispiele
Laminate mit zwei Schichten
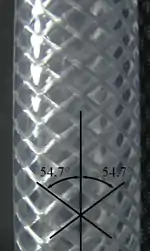
Es gibt unendlich viele Möglichkeiten, Laminate herzustellen, die einen gegebenen Spannungszustand ertragen können. Der Spannungszustand darf sich jedoch nicht ändern, da das Laminat sonst nicht mehr netztheoretisch tragfähig ist. Die Bedingung für die beiden Schichtwinkel lautet:
Oft fordert man, dass beide Winkel vom Betrag gleich groß sein sollen . Auf diese Weise erhält man immer einen ausgeglichenen Winkelverbund. Für das Normalspannungsverhältnis 1:2, das bei innendruckbelasteten Rohren auftritt (Kesselformel), ergibt sich demnach als Winkel (siehe Bild). Diesen Winkel findet man bei praktisch allen gewickelten Rohren und Behältern wieder. Es sind jedoch auch andere Winkel z. B. möglich. Diese Lösungen sind gleichwertig.
Laminate mit drei Schichten
Dieser Fall ist nur dann behandelbar, wenn ein ausgeglichener Winkelverbund und eine unidirektionale Schicht verwendet werden. Auf diese Weise schafft man es, die Anzahl der unbekannten Schichtwinkel und -dicken so zu reduzieren, dass das Gleichungssystem lösbar wird.
Ein Laminat aus drei Schichten ist nicht zwingend optimal. Es muss besonders beachtet werden, dass die Regel 3 und 4 nicht verletzt werden. Hat eine Schicht ein unterschiedliches Vorzeichen, ist das Laminat nicht mehr optimal.
Hinweis
Obiger Artikel ist nur ein kurzer Abriss über die Eigenschaften der Netztheorie. Eine vertiefende Behandlung findet sich in zahlreichen Lehrbüchern des Leichtbaus.
Literatur
- J. Wiedemann: Leichtbau, Band 1&2. Springer-Verlag, Berlin 1986.