Intensitätsinterferometer

Das Intensitätsinterferometer, auch Korrelationsinterferometer genannt, ist ein optisches Gerät (Interferometer) zur Bestimmung des Winkeldurchmessers astronomischer Objekte (in der Regel Sterne), die bei direkter Beobachtung nicht aufgelöst werden können.

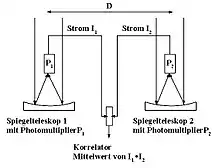
Strahlengang im Intensitätsinterferometer

Intensitätsinterferometrie von α Lyrae (Wega) und β Crucis (Mimosa)

Prinzip

Das Intensitätsinterferometer besteht aus zwei räumlich getrennten Teleskopen, an welchen jeweils mittels eines Photomultipliers die Ankunftszeiten der dort von einem hellen Stern eintreffenden Photonen registriert werden, was praktisch durch die Aufzeichnung des zeitlichen Verlaufs der beiden dort anfallenden Ströme geschieht. Diese werden in einem Korrelator zusammengeführt, welcher die beiden Zeitverläufe auf Koinzidenzen hin untersucht. Aus der Korrelation zwischen den beiden Strömen kann auf den Winkeldurchmesser des Sterns geschlossen werden (siehe weitergehende Erläuterungen unten).

Robert Hanbury Brown und Richard Twiss erkannten Mitte der 1950er Jahre[1], dass die Austrittszeiten der Elektronen an verschiedenen Stellen einer von einer ebenen Welle ausgeleuchteten Photokathode miteinander korreliert sind. Sie zeigten, dass dieser Effekt – der nach seinen Entdeckern Hanbury Brown-Twiss-Effekt genannt wird – sowohl durch die klassische Wellentheorie des Lichts als auch durch dessen Quantennatur gedeutet werden kann.

Laut der Arbeit von 1957 spiegeln die miteinander korrelierten Austrittszeiten der Elektronen klassisch gesehen miteinander korrelierte Intensitätsschwankungen wider, welche an verschiedenen Stellen der einfallenden Welle auftreten. Diese sind auf Interferenzen verschiedener Frequenzkomponenten des einfallenden Lichts zurückzuführen. Quantenmechanisch gesehen beruht der Effekt darauf, dass Photonen der Bose-Einstein-Statistik folgen und damit die Tendenz zeigen, gehäuft aufzutreten (was oft als Photon Bunching bezeichnet wird).

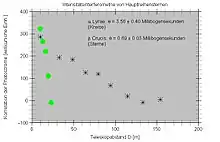
In einer nachfolgenden Arbeit[2] legten die beiden Forscher dar, wie sich der von ihnen entdeckte Effekt zur Messung des Winkeldurchmessers eines Sterns nutzen lässt. Sind die beiden Ströme stark miteinander korreliert (was bedeutet, dass Photonen häufig gleichzeitig an beiden Empfängern eintreffen), so ist der beobachtete Stern noch nicht aufgelöst. Dies ist dann der Fall, wenn der Abstand $D$ der beiden Teleskope zu gering ist. Wird dieser vergrößert, nimmt die Korrelation zwischen den Strömen (das heißt der Ankunftszeiten der Photonen) ab. Aus dem Abfall der Korrelation mit zunehmendem Abstand kann der Winkeldurchmesser $\theta$ des Sterns bestimmt werden. Dieser ist[3] eine Funktion des Ausdruckes $\pi \theta D/\lambda$ ( $\lambda$ bezeichnet die Wellenlänge des einfallenden Lichts). Hat ein Stern z. B. den doppelten Winkeldurchmesser im Vergleich zu einem anderen, so muss man die Teleskope nur halb so weit auseinanderzuziehen, um den gleichen Korrelationsabfall zu beobachten.

Schließlich sei mit den Sternen α Lyrae (Wega) und β Crucis (Mimosa) auch ein praktisches Beispiel[4] erwähnt. Bei Ersterem fällt die Korrelation der einzelnen Ströme schon bei einem Teleskopabstand von etwa 20 m praktisch auf null ab. Bei Letzterem muss man diese etwa 100 m voneinander entfernen, um den gleichen Effekt zu erzielen. Folglich hat Wega einen weit größeren Winkeldurchmesser als Mimosa.

Messgenauigkeit

Die durch die Ankunftszeiten der Photonen bedingten korrelierten Intensitätsschwankungen werden durch weit stärkere nicht miteinander korrelierte Schwankungen überlagert. Eine Quelle dieser zusätzlichen Schwankungen ist die Luftunruhe, welche das alltägliche Funkeln der Sterne verursacht (Szintillation), eine andere das Schrotrauschen der von den beiden Photomultipliern ausgehenden Ströme. Die dadurch bedingten Fluktuationen übertreffen die eigentlich gesuchten korrelierten Schwankungen bei weitem, um etwa einen Faktor 100.000.[5] Die nicht miteinander korrelierten Zusatzschwankungen können durch sehr lange Beobachtungszeiten „weggemittelt“ werden, doch selbst bei sehr hellen, mit bloßem Auge leicht sichtbaren Sternen (nicht schwächer als 2. Größe) waren Belichtungszeiten von bis zu 100 Stunden erforderlich.[6] Eine außerordentliche Stabilität der Messelektronik, insbesondere des Korrelators, ist daher für das Instrument extrem wichtig.

Glücklicherweise hat[7] die Luftunruhe kaum Einfluss darauf, wie schnell die Korrelation zwischen den Einzelströmen mit zunehmendem Abstand der Teleskope abfällt. Somit erzwingt die Luftunruhe zwar sehr lange Belichtungszeiten, verfälscht aber nicht das Aussehen der Kurve (und damit den daraus abgeleiteten Winkeldurchmesser des Sterns), welche die Korrelation als Funktion von $D$ und $\theta$ beschreibt.

Die Genauigkeit, mit welcher der Winkeldurchmesser eines Sterns ermittelt werden kann, ist durch das Verhältnis von Lichtwellenlänge zu maximalem Teleskopabstand $\lambda /D_{\mathrm {max} }$ gegeben. Mit $\lambda$ = 440 nm und $D_{\mathrm {max} }$ = 188 m (für das Instrument der 60er Jahre) erwartet man $\lambda /D_{\mathrm {max} }$ = 0,0005". In der Praxis erreichten Hanbury Brown noch eine etwas bessere Genauigkeit, nämlich im Mittel 0,0002".[8] Damit übertrifft das Intensitätsinterferometer das klassische Michelson-Sterninterferometer bei weitem und erlaubt auch die Einbeziehung sonnennaher Hauptreihensterne. Während das Auflösungsvermögen des Michelson-Sterninterferometers durch die Luftunruhe beschränkt ist (es kommt hier auf das Abbild des Sterns in Form eines Interferenzmusters an), ist dies bei dem Intensitätsinterferometer nicht der Fall. Es interessiert nur die Intensität des Sterns, nicht dessen bildliche Wiedergabe.

Um die Messergebnisse des Intensitätsinterferometers richtig zu deuten, muss wie bei dem Michelson-Sterninterferometer die Randverdunklung (der Abfall der Intensität der Sternscheibe von der Mitte zum Rand) beachtet werden. Gemäß Hanbury Browns Publikationen von 1967 hat diese zur Folge, dass die Korrelation der beiden Einzelströme bei dem Auseinanderziehen der Teleskope langsamer abfällt, als man dies bei einer gleichförmig leuchtenden Sternscheibe erwarten würde, d. h. der Winkeldurchmesser wird unterschätzt. Die Art der mathematischen Gesetzmäßigkeit zwischen Korrelation und Teleskopabstand bleibt jedoch unverändert, sie erhält lediglich eine längere Skala bezüglich $D$ . Das Interferometer liefert also einen effektiven Winkeldurchmesser – welchen der Stern haben würde, wenn dessen Scheibe bei gleicher Gesamtintensität gleichförmig leuchtete. Um aus dem effektiven Winkeldurchmesser den tatsächlichen bestimmen zu können, ist ein Modell der Sternatmosphäre erforderlich. Bei den von Hanbury Brown (1967b) gemessenen Hauptreihensternen beträgt die Modifikation des Winkeldurchmessers aber nur wenige Prozent.

Geschichte

Nach den theoretischen Vorarbeiten in den 1950er Jahren gelang bald auch eine erfolgreiche Testmessung des Sirius.[9] Das erste voll einsatzfähige Gerät seiner Art ging 1962 in Narrabri (Australien) in Betrieb. Der Aufbau und die Inbetriebnahme des Interferometers erwiesen sich als eine schwierige Herausforderung, allein diese Phase erstreckte sich über fast zwei Jahre.[10] Es folgte eine wiederum zweijährige Phase von Testmessungen mehrerer Hauptreihensterne, erst 1965 startete das eigentliche Beobachtungsprogramm. 1967 erfolgte die erste Veröffentlichung von Winkeldurchmessern von 15 Hauptreihensternen.[8] Insgesamt wurden bis 1972 die Winkeldurchmesser von 32 Hauptreihensternen bestimmt.[11]

Das Interferometer bestand aus zwei Reflektoren von je 6,7 m Durchmesser, die aus je 252 sechseckigen Einzelspiegeln zusammengesetzt wurden.[12] Die beiden Instrumente konnten auf einem Schienenkreis bis zu 188 m voneinander entfernt werden.

1990 wurde als Nachfolgeinstrument das Sydney University Stellar Interferometer SUSI in Betrieb genommen. Es befindet sich auf dem Observatorium Culgoora in der Nähe von Narrabi. Es handelt sich hierbei jedoch nicht um ein Intensitätsinterferometer, sondern um ein modernes Michelson-Interferometer, welches durch adaptive Optik den Mangel des klassischen Interferometers, die Störung des Interferenzbilds durch die Luftunruhe, überwindet[13]. Gleichzeitig ist es weit empfindlicher als das Narrabi-Interferometer, es erlaubt die Messung von Sternen bis etwa zur 8. Größenklasse. Der maximale Abstand der zur Interferenz gebrachten Lichtwege beträgt 640 m. Eine Beschreibung des SUSI findet sich unter Michelson-Sterninterferometer.

Die Messung des Winkeldurchmessers eines Sterns und damit bei bekannter Entfernung auch dessen Radius führt zwangsläufig zu der Frage, was eigentlich unter der Oberfläche eines Sterns zu verstehen ist. Dieses angesichts des Fehlens einer festen Kruste alles andere als triviale Problem wird unter Sternoberfläche diskutiert.

Quellen

Hanbury Brown R.: A Test of a new Type of Stellar Interferometer on Sirius, in: Nature Band 178, S. 1046ff, 1956
Hanbury Brown R., Twiss R. G.: Correlation between Photons in two Coherent Beams of Light, in: Nature Band 177, S. 27ff, 1956
Hanbury Brown R., Twiss R. G.: Interferometry of the Intensity Fluctuations in Light. I. Basic Theory: the Correlation between Photons in Coherent Beams of Radiation, in: Proceedings of the Royal Society of London Band 242, S. 300ff, 1957
Hanbury Brown R., Twiss R. G.: Interferometry of the Intensity Fluctuations in Light. III. Applications to Astronomy, in: Proceedings of the Royal Society of London Band 248, S. 199ff, 1958
Hanbury Brown R., Davis J., Allen L. R.: The Stellar Interferometer at Narrabi Observatory. I. A Description of the Instrument and the Observational Procedure, in: Monthly Notices of the Royal Astronomical Society Band 137, S. 3 75ff, 1967a, bibcode:1967MNRAS.137..375H
Hanbury Brown R., Davis J., Allen L. R., Rome J. M.: The Stellar Interferometer at Narrabi Observatory. II. The Angular Diameters of 15 Stars, in: Monthly Notices of the Royal Astronomical Society Band 137, S. 393ff, 1967b, bibcode:1967MNRAS.137..393H
Hanbury Brown R., Davis J., Allen L. R.: The Angular Diameters of 32 Stars, in: Monthly Notices of the Royal Astronomical Society Band 167, S. 121ff, 1974, bibcode:1974MNRAS.167..121H
Davis J., Tango W. J., Booth A. J., ten Brummelaar T. A., Minard A. R., Owens S. M.: The Sydney University Stellar Interferometer – I. The instrument, in: Monthly Notices of the Royal Astronomical Society Band 303, S. 773ff, 1999

Weblinks

Private Internetseite über den Hanbury Brown-Twiss-Effekt. Anmerkung: Die dort gemachten Aussagen hinsichtlich des Photon Bunchings und der Bose-Einstein-Statistik stehen im Widerspruch zu der Arbeit von Hanbury Brown und Twiss (1957)!

Einzelnachweise

siehe Hanbury Brown und Twiss (1956) sowie Hanbury Brown und Twiss (1957)
siehe Hanbury Brown und Twiss (1958) sowie auch Hanbury Brown et al. (1967a)
laut der Arbeit von 1967
von Hanbury Brown et al. (1967b)
gemäß Hanbury Brown et al. (1967a)
siehe Hanbury Brown et al. (1967b)
laut Hanbury Brown et al. (1967a)
Hanbury Brown et al. (1967b)
siehe Hanbury Brown (1956)
laut Hanbury et al. (1967a)
siehe Hanbury Brown et al. (1974)
Hanbury Brown et al. (1967a)
siehe Davis et al. (1999)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] siehe Hanbury Brown und Twiss (1956) sowie Hanbury Brown und Twiss (1957)

[2] siehe Hanbury Brown und Twiss (1958) sowie auch Hanbury Brown et al. (1967a)

[3] ut der Arbeit von 1967

[4] von Hanbury Brown et al. (1967b)

[5] äß Hanbury Brown et al. (1967a)

[6] siehe Hanbury Brown et al. (1967b)

[7] ut Hanbury Brown et al. (1967a)

[Hanbury_Brown_et_al._1967b-8] Hanbury Brown et al. (1967b)

[9] siehe Hanbury Brown (1956)

[10] ut Hanbury et al. (1967a)

[11] siehe Hanbury Brown et al. (1974)

[12] Hanbury Brown et al. (1967a)

[13] siehe Davis et al. (1999)