Michelson-Sterninterferometer
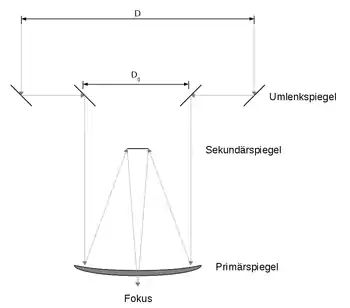

Prinzip
Das Michelson-Sterninterferometer ist eines der frühesten in der Astronomie eingesetzten Interferometer. Es beruht darauf, dass das Licht eines Sterns auf zwei getrennten Wegen aufgenommen wird, welche zur Interferenz gebracht werden. Die beiden Wege werden durch zwei spaltförmige Öffnungen erzeugt, welche einen Abstand voneinander haben. Mittels je zweier Umlenkspiegel gelangen die beiden Lichtpfade auf den Primärspiegel des Teleskops, von dort aus auf den Sekundärspiegel und laufen schließlich im Fokus zusammen.
Wäre ein Stern eine Punktquelle, so würde die Überlagerung der beiden Lichtwege ein dem Doppelspaltexperiment entsprechendes Interferenzmuster erzeugen. Es würde eine Anordnung von Streifen entstehen, welche einen Winkelabstand aufweisen würden ( bezeichnet die Wellenlänge des einfallenden Lichts). Tatsächlich aber haben Sterne trotz ihrer großen Entfernungen einen zwar winzigen, aber doch nicht verschwindenden Winkeldurchmesser. Jeder Punkt der Sternoberfläche liefert ein eigenes Interferenzmuster, so dass eine Vielzahl von Streifenmustern entsteht. Diese aber sind gegeneinander verschoben, gemäß dem Winkelabstand der entsprechenden Punkte auf der Sternoberfläche. Die Überlagerung der einzelnen Streifensysteme hat zur Folge, dass kein Interferenzmuster mehr zu erkennen ist, wenn der Winkeldurchmesser des Sterns gleich ist. Die Messung erfolgt dadurch, dass der Abstand der beiden Spaltöffnungen solange variiert wird, bis das Interferenzmuster verschwindet.
Messgenauigkeit
Infolge der Luftunruhe weist das klassische Verfahren nach heutigem Maßstab nur eine mäßige Genauigkeit auf. Gemäß Hale (1921) betrug die Genauigkeit bei der erstmaligen Messung des Winkeldurchmessers von Beteigeuze etwa 0,005″. Scheffler und Elsässer (1990) zufolge kann der Messfehler bei bis zu 0,01″ liegen (moderne Instrumente erreichen, wie nachfolgend gezeigt wird, eine Genauigkeit von bis zu 0.00002″, sind also bis zu 500 mal präziser als das klassische Interferometer). Die Unsicherheit entspricht damit etwa dem Winkeldurchmesser, unter dem die Sonne vom nächsten Stern aus erscheint. Damit ist klar, dass das Michelson-Sterninterferometer bei Hauptreihensternen generell versagt, und auch im Bereich der Riesen und Überriesen nur relativ nahe Objekte mit Entfernungen bis zu etwa 100 Parsec zuverlässig gemessen werden können.
Um aus dem Winkeldurchmesser den tatsächlichen Durchmesser des Sterns abzuleiten, müssen weitere Effekte berücksichtigt werden. Eine Erschwernis stellt insbesondere die sogenannte Randverdunklung dar, worauf bereits Hale (1921) hingewiesen hat. Die Mitte der Sternscheibe leuchtet heller als der Rand, trägt somit stärker zum Interferenzmuster bei. Es besteht die Tendenz, den Durchmesser des Sterns zu unterschätzen.
Gerade die der Interferometrie noch am zugänglichsten Riesen und Überriesen weisen oft ausgedehnte Photosphären auf und stellen damit im Gegensatz zur Sonne ausgesprochen diffuse Objekte dar. Nun besteht die Tendenz, den Durchmesser zu überschätzen, da die Messung nicht nur den eigentlichen Sternkörper, sondern auch dessen Hülle mit einbezieht. Auf die daraus folgende Problematik, wie der Durchmesser eines solchen Sterns überhaupt zu definieren ist, wird im Artikel Sternoberfläche ausführlich eingegangen.
Natürlich muss auch die Entfernung des Sterns bekannt sein, um den Winkeldurchmesser in den tatsächlichen umzurechnen. Als das Michelson-Sterninterferometer zum Einsatz kam, war auch die Kenntnis der Entfernung gerade von Riesen und Überriesen sehr unsicher. So unterschieden sich die von Pease (1921) zusammengestellten Entfernungsangaben für den Roten Riesen Arktur um mehr als 100 % (6,3 bis 13,5 Parsec entsprechend 21 bis 44 Lichtjahren). In den 1990er Jahren konnten mittels des Hipparcos-Satelliten für mehr als 100 000 Sterne fast aller Typen zuverlässige Entfernungen bestimmt werden. Die ausgedehnten Photosphären mancher Sterne stellen jedoch auch für heutige Instrumente eine erhebliche Begrenzung der Messgenauigkeit dar.
Geschichte
Das Michelson-Sterninterferometer wurde im Jahre 1890 von Albert A. Michelson entworfen. Über 20 Jahre früher hatte bereits Hippolyte Fizeau der französischen Académie des sciences einen Vorschlag zur Interferometrie an Sternen unterbreitet, der dann von M. Stephan, dem damaligen Direktor des Observatoriums von Marseille umgesetzt worden war. Unklar ist, ob Michelson von diesen Vorarbeiten wusste.[1]
Mit einer Schlitzblende an einem 12-Zoll-Teleskop führte Michelson 1891 Testmessungen der Durchmesser der vier Galileischen Jupitermonde durch, die eine vorzügliche Übereinstimmung mit den bereits auf andere Weise bestimmten Werten ergaben. Allerdings dauerte es nach diesen ersten Vorarbeiten noch 25 Jahre, bis das erste Michelson-Sterninterferometer praktisch eingesetzt wurde: eine Anordnung, mit der Licht von rund 6 Meter auseinanderliegenden Planspiegeln in das 2,5-Meter-Spiegelteleskop des Mount-Wilson-Observatoriums reflektiert wurde.
Mit diesem Gerät führten Michelson und Francis G. Pease (1881–1938) die ersten Messungen von Sterndurchmessern durch. Die erste solche Messung betraf den Durchmesser von Beteigeuze, den Michelson und Pearse im Dezember 1920 zu 390 Millionen Kilometern bestimmten. Das entspricht in etwa dem Durchmesser der Marsbahn; damit ist der rote Riese Beteigeuze rund 300 mal größer als die Sonne. Hale (1921) schildert, dass bei einem Abstand der beiden Spaltöffnungen von 6 Fuß noch klar ein Interferenzmuster zu erkennen war. Bei einem Abstand von 8 Fuß war dieses bereits weit schwächer ausgeprägt, und bei einem Abstand von 10 Fuß ganz verschwunden. Mit einer mittleren Wellenlänge von 550 nm konnte daraus ein Winkeldurchmesser von 0,045″ abgeleitet werden.
Sechs weitere Sterndurchmesser folgten. Auf diese ersten Erfolge folgte die Konstruktion eines noch größeren Geräts, dessen Spiegel nun schon ganze 15 Meter auseinanderlagen. Allerdings gelang mit dieser verbesserten Apparatur nur die Messung eines einzigen zusätzlichen Sterndurchmessers, und die entsprechenden Beobachtungsreihen wurden 1931 eingestellt.[2]
Moderne Interferometer
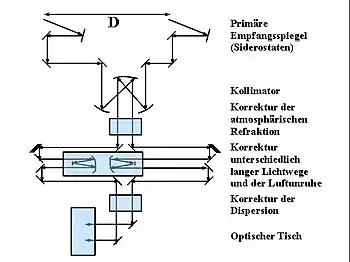
Seit den 1990er Jahren erlebt das Michelson-Sterninterferomter eine Renaissance. Möglich wurde dies durch die adaptive Optik, welche eine Echtzeitkorrektur der durch die Luftunruhe bedingten Beeinträchtigungen gestattet. Als Beispiel sei hier das am Observatorium Culgoora in Australien betriebene Sydney University Stellar Interferometer SUSI diskutiert, welches bei Davis et al. (1999) ausführlich beschrieben ist.
Als primäre Empfangsspiegel, welchen den Abstand definieren, dienen Siderostaten, welche unabhängig von der Position des Sterns am Himmel immer in die gleiche Richtung reflektieren. Ihr Durchmesser beträgt 20 cm, wozu aber nur 14 cm effektiv beitragen, weil das Sternenlicht nicht senkrecht, sondern unter einem bestimmten Winkel einfällt. Die geringe Größe ist bewusst gewählt: Das Auflösungsvermögen des Einzelspiegels ist nicht mehr durch die Luftunruhe, sondern durch die Beugung begrenzt. Dadurch bewirkt die Luftunruhe nicht mehr wie bei einem großen Teleskop ein „Wabern“ des Sternbildes, sondern nur noch ein Hin- und Herwackeln desselben als Ganzes, was durch die adaptive Optik leichter zu analysieren und korrigieren ist. Das Instrument verfügt über 12 ortsfeste Siderostaten, welche linear in Nord-Süd-Richtung angeordnet sind. Durch Auswahl eines jeweils unterschiedlichen Spiegelpaars können verschiedene Abstände von 5–640 m realisiert werden.
Von den Siderostaten gelangen die einfallenden Strahlenbündel in einen aus zwei Parabolspiegeln bestehenden Kollimator. Dort werden die Durchmesser der Strahlenbündel von ursprünglich 14 cm auf 5 cm reduziert und so diese an die nachfolgenden, recht kleinen optischen Elemente angepasst. Anschließend passieren sie ein hier nicht weiter diskutiertes System, welches die von der Atmosphäre hervorgerufenen Effekte der Lichtbrechung korrigiert.
Im Gegensatz zu den Primärspalten des klassischen Interferometers sind bei dem Culgoora Instrument die Siderostaten asymmetrisch platziert, was zunächst unterschiedlich lange Wege für die beiden Strahlenbündel zur Folge hat. Diese Asymmetrie wird durch ein aus zwei fahrbaren Reflektoren bestehendes System beseitigt. Je nachdem wie weit diese von der optischen Achse entfernt sind, wird für einen Strahl der Weg verkürzt, und für den anderen in gleichem Maße verlängert. Die Korrektur der Lichtwege schließt auch ein adaptives Element mit ein. Die mit fetten Linien dargestellten Spiegel können bewegt und dadurch in Echtzeit die durch die Luftunruhe bewirkte Bildbewegung vermindert werden.
Nun durchlaufen die beiden Strahlen ein System zur Korrektur der Dispersion, was hier ebenfalls nicht näher erläutert wird. Schließlich erreichen sie das Herzstück des Instruments, den von Davis et al. (1999) so genannten „Optischen Tisch“.
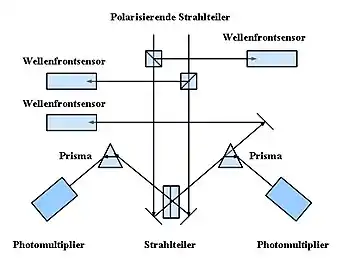
In diesem „Optischen Tisch“ werden die Strahlen zur Interferenz gebracht. Zuvor aber passieren sie jeweils einen polarisierenden Strahlteiler, der sie in horizontal und vertikal polarisierte Komponenten zerlegt. Die horizontal polarisierten Komponenten gelangen zur Interferenz, die vertikal polarisierten Anteile werden Wellenfrontsensoren (siehe unter adaptive Optik) zugeleitet, welche die Bildbewegung analysieren.
Um die verbliebenen horizontal polarisierten Komponenten zur Interferenz zu bringen, wird ein weiterer Strahlteiler eingesetzt. Es entstehen zwei neue Strahlen, welcher aber Anteile beider der ursprünglichen Bündel besitzen. Prismen leiten jeden der neuen Strahlen in jeweils einen Photomultiplier um. Dabei unterliegt aber nicht die gesamte einfallende Energie der Brechung, ein kleiner Teil verlässt das Prisma mit unveränderter Richtung. Letzterer wird für einen der beiden neuen Strahlen einem dritten Wellenfrontsensor zugeführt. Durch Vergleich mit den Ergebnissen der beiden anderen Sensoren (welche die Bildbewegung vor der Interferenz untersuchen) kann der Einfluss der Luftunruhe auch nach der Zusammenführung der Originalstrahlen analysiert werden.
Die Bestimmung des Winkeldurchmessers des Sterns erfolgt nun dadurch, dass die Intensitäten der beiden neuen Strahlen gemessen und zeitlich miteinander korreliert werden. Diese Korrelationsmessung darf nicht mit derjenigen des Intensitätsinterferometers verwechselt werden. Bei letzterem werden die einfallenden Strahlen schon vor der Interferenz in Intensitäten umgewandelt, bei dem Michelson-Interferometer aber erst danach! Die Korrelation zwischen den beiden Intensitäten zeigt aber bei beiden Instrumententypen das gleiche qualitative Verhalten. Ist der Abstand zwischen den Primärempfängern sehr gering, sind die beiden Intensitäten zeitlich stark miteinander korreliert. Dies bedeutet im klassischen Sinne, dass das durch das Michelson-Interferometer erzeugte Interferenzmuster klar sichtbar ist. Vergrößert man den Abstand, nimmt die Korrelation, das heißt die Sichtbarkeit des Interferenzmusters ab. Je größer der Winkeldurchmesser des Sterns ist, umso geringer ist der erforderlich Abstand , um einen Korrelationsabfall zu erzielen.
Aufgrund der zahlreichen Korrekturelemene, insbesondere der adaptiven Optik, erreicht das SUSI eine außerordentliche Genauigkeit. So bestimmten Davis et al. (2009) den Winkeldurchmesser des Cepheiden 1 Car mit einem Messfehler von nur 0.00002″! Damit ist es auch möglich, durch Pulsation hervorgerufene zeitliche Veränderungen genau zu beobachten. Es gilt jedoch weiterhin, dass der nominelle Winkeldurchmesser vom Einfluss der Randverdunklung und einer eventuell vorhandenen ausgedehnten Sternatmosphäre befreit werden muss.
Moderne Michelson-Sterninterferometer überwinden aber nicht nur den Mangel des klassischen Vorgängers (die vergleichsweise hohe Unsicherheit des Winkeldurchmessers), sie vermeiden auch das Handikap des Intensitätsinterferometers (die sehr geringe Empfindlichkeit). Während das Intensitätsinterferometer nur für sehr helle Sterne bis 2. Größe einsetzbar war, können mit SUSI Sterne bis zur 8. Größe gemessen werden. Damit sind mehrere 10.000 Objekte praktisch aller Spektraltypen zugänglich, deren Entfernungen zudem dank der Messungen des Hipparcos-Satelliten zumeist bekannt sind.
Von der Interferometrie zur Apertursynthese
Die bei Michelsons Sterninterferometer entwickelten Prinzipien führten ab den 1950er Jahren zur Entwicklung der Apertursynthese für Radioteleskope durch Martin Ryle, und ab den 1960er Jahren zu Entwicklungen optischer interferometrischer Methoden, deren moderne Nachfahren Teleskope wie das Large Binocular Telescope und das VLT-Interferometer sind.[3]
Der Grundgedanke der Apertursynthese besteht darin, nicht nur zwei, sondern zumindest drei Primärstrahlen zur Interferenz zu bringen. Das dabei entstehende sehr komplexe Interferenzmuster erlaubt nicht nur, den Winkeldurchmesser des beobachteten Objekts zu bestimmen, sondern auch dessen Intensitätsverteilung (d. h. dieses tatsächlich als flächig erscheinenden Körper darzustellen). Im Radiobereich, in dem Störungen durch die Atmosphäre keine Rolle spielen, wird dieses Verfahren bereits seit mehreren Jahrzehnten eingesetzt. Im sichtbaren Licht und nahen Infraroten hat erst die adaptive Optik der Apertursynthese den Weg geebnet. Als Beispiel sei die Arbeit von Haubois et al. (2009) genannt, welche mit einem aus drei Teleskopen bestehenden Interferometer die Oberfläche von Beteigeuze im nahen Infraroten auflöste.
Angesichts des Fehlens einer festen Kruste muss bei interferometrische Sternmessungen generell die Frage beachtet werden, was unter einer Sternoberfläche eigentlich zu verstehen ist. Darauf wird im entsprechenden Artikel eingegangen.
Siehe auch
Literatur
- J. Davis, W.J. Tango, A.J. Booth, T.A. ten Brummelaar, R.A. Minard, S.M. Owens: The Sydney University Stellar Interferometer: I. The instrument. In: Monthly Notices of the Royal Astronomical Society 303, 1999, S. 773ff
- J. Davis, A.P. Jacob, J.G. Robertson, M.J. Ireland, J.R. North, W.J. Tango, P.G. Tuthill: Observations of the pulsation of the Cepheid l Car with the Sydney University Stellar Interferometer. In: Monthly Notices of the Royal Astronomical Society 394, 2009, S. 1620ff
- X. Haubois, G. Perrin, S. Lacour, T. Verhoelst, S. Meimon, L. Mugnier, E. Thiébaut, J.P. Berger, S.T. Ridgway, J.D. Monnier, R. Millan-Gabet, W. Traub: Imaging the spotty surface of Betelgeuse in the H band. In: Astronomy and Astrophysics Band 505, 2009, S. 923ff
- G.E. Hale: The Angular Diameter of Alpha Orionis. In: Monthly Notices of the Royal Astronomical Society Band 81, 1921, S. 166ff
- A. Labeyrie, S.G. Lipson, P. Nisenson: An Introduction to Optical Stellar Interferometry. Cambridge University Press, Cambridge 2006, ISBN 0-521-82872-4.
- F.G. Pease: The Angular Diameter of Alpha Bootis by the Interferometer. In: Publications of the Astronomical Society of the Pacific Band 33, 1921, S. 171ff
- H. Scheffler, H. Elsässer: Physik der Sterne und der Sonne. BI Wissenschaftsverlag, Mannheim / Wien / Zürich, 2. Auflage 1990, ISBN 3-411-14172-7.
Der Artikel verwendet Informationen aus dem Eintrag Michelson stellar interferometer der englischsprachigen Wikipedia, Stand 8. Dezember 2008.
Einzelnachweise
- Labeyrie et al. 2006, S. 2f.
- Labeyrie et al. 2006, S. 4ff.
- M. Ryle: Radio Telescopes of Large Resolving Power. Nobelpreis-Vortrag, 12. Dezember 1974. Zum LBT siehe K. Jäger, Wissenschaftliche Beobachtungen am LBT gestartet. In: Sterne und Weltraum Bd. 7/2007, S. 16–18. Zum VLT-Interferometer siehe A. Glindemann: Das VLT-Interferometer. In: Sterne und Weltraum Bd. 3/2003, S. 24–32.