Satz vom Fußball

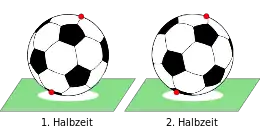
Der Satz vom Fußball ist ein mathematischer Satz aus der linearen Algebra und Geometrie, der auf anschauliche Weise die Eigenschaften der Drehgruppe $\mathrm {SO} (3)$ illustriert. Der Satz gibt die Existenz zweier Fixpunkte auf einer Kugeloberfläche an, nachdem die Kugel beliebig oft am Platz gedreht worden ist. Die mathematische Grundaussage des Satzes wurde mit Hilfe elementarer geometrischer Argumente erstmals im Jahr 1776 von dem Schweizer Mathematiker Leonhard Euler bewiesen.[1]

Nach dem Satz vom Fußball gibt es zwei Punkte auf einem Fußball (hier rot markiert), die sich zu Beginn der ersten und der zweiten Halbzeit an derselben Stelle im Raum befinden.

Aussage

Der Satz vom Fußball lautet wie folgt:

„Bei jedem Fußballspiel gibt es zwei Punkte auf der Oberfläche des Balls, die sich zu Beginn der ersten und der zweiten Halbzeit, wenn der Ball genau auf dem Anstoßpunkt liegt, an derselben Stelle im umgebenden Raum befinden.“[2][3]

Beweis

Beweisidee

Rotation einer Kugel um eine Drehachse

Im Folgenden wird der Fußball idealisiert als Kugel dargestellt. Im Verlauf der ersten Halbzeit führt ein Fußball eine Reihe von Bewegungen im Raum durch. Da der Fußball zu Beginn der zweiten Halbzeit wieder zurück auf den Anstoßpunkt gelegt wird, können im Weiteren die Verschiebungen des Balls außer Betracht bleiben und es brauchen nur die Drehungen des Balls betrachtet zu werden. Jede dieser Drehungen kann durch eine Drehachse und einen Drehwinkel beschrieben werden. Punkte im Raum, die sich auf der Drehachse befinden, verändern bei einer Drehung ihre Position nicht.

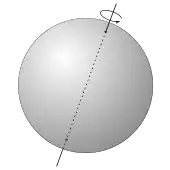
Eine wichtige Eigenschaft des dreidimensionalen Raums ist nun, dass jede Hintereinanderausführung von zwei oder mehreren Drehungen durch eine einzige Drehung beschrieben werden kann. Die Drehachse dieser Drehung durchstößt dabei die Oberfläche des Fußballs an zwei diametral gegenüberliegenden Punkten (Antipoden). Diese beiden Punkte müssen sich demnach zu Beginn der ersten und der zweiten Halbzeit an derselben Stelle im Raum befinden.[3]

Beweis

Nach Wahl eines kartesischen Koordinatensystems mit dem Kugelmittelpunkt als Koordinatenursprung kann jede Drehung im Raum durch eine Drehmatrix $D\in \mathbb {R} ^{3\times 3}$ beschrieben werden. Eine Drehmatrix ist dabei eine orthogonale Matrix mit Determinante $\det D=1$ . Führt eine Kugel insgesamt $n$ Drehungen durch, dann können diese durch $n$ Drehmatrizen $D_{1},\ldots ,D_{n}$ angegeben werden. Die Hintereinanderausführung dieser Drehungen entspricht dann dem Matrizenprodukt

Q=D_{n}\cdot \ldots \cdot D_{1}

der Drehmatrizen. Weil das Produkt zweier orthogonaler Matrizen wieder orthogonal ist (siehe orthogonale Gruppe) und die Determinante des Produkts zweier Matrizen gleich dem Produkt der Determinanten ist (Determinantenproduktsatz), ist auch die Matrix $Q$ wieder eine orthogonale Matrix mit Determinante $\det Q=1$ . Sind nun $\lambda _{1},\lambda _{2}$ und $\lambda _{3}$ die drei (im Allgemeinen komplexen) Eigenwerte von $Q$ , dann gilt

1=\det Q=\lambda _{1}\cdot \lambda _{2}\cdot \lambda _{3}

.

Da für die Eigenwerte einer orthogonalen Matrix $|\lambda |=1$ gilt und komplexe Eigenwerte paarweise komplex konjugiert auftreten, muss mindestens ein Eigenwert von $Q$ reell und gleich $1$ sein. Dies bedeutet wiederum, dass es einen Eigenvektor $x\in \mathbb {R} ^{3}\setminus \{0\}$ geben muss, für den

Q\,x=1\,x

gilt. Ein solcher Vektor $x$ und jedes skalare Vielfache dieses Vektors wird demnach durch die Matrix $Q$ auf sich selbst abgebildet. Die lineare Hülle $\langle x\rangle$ dieses Vektors definiert eine Ursprungsgerade, die die Kugeloberfläche in zwei Punkten schneidet. Dies sind die beiden gesuchten Punkte, die bei der Gesamtdrehung festgehalten werden.[3]

Verwendung

Der Satz vom Fußball wird in der neueren mathematischen Literatur häufig als Korollar, das heißt als unmittelbare Folgerung aus vorher bewiesenen Sätzen, angegeben. In einem solchen Fall erweist sich der Beweis des Satzes meist als recht einfach. Gerd Fischer schreibt etwa in seinem Lehrbuch zur linearen Algebra, dass der Satz vom Fußball leichter zu beweisen als anschaulich zu verstehen sei, und beweist ihn dann in einer Zeile.[2]

Der Satz vom Fußball ist ein Spezialfall einer allgemeineren Aussage, nach der in einem endlichdimensionalen reellen Skalarproduktraum die orthogonalen Endomorphismen mit positiver Determinante eine Gruppe, die sogenannte spezielle orthogonale Gruppe $\mathrm {SO} (n)$ , bilden. Ist die Dimension $n$ des zugrunde liegenden Vektorraums ungerade, dann hat jede Abbildung in dieser Gruppe den Eigenwert $1$ .

Siehe auch

Literatur

Gerd Fischer: Lineare Algebra: Eine Einführung für Studienanfänger. 18. Auflage. Springer Spektrum, Wiesbaden 2013, ISBN 978-3-658-03944-8.
Michael Merz, Mario V. Wüthrich: Mathematik für Wirtschaftswissenschaftler. Vahlen, München 2013, ISBN 978-3-8006-4483-4.

Einzelnachweise

Leonhard Euler: Novi Commentarii academiae scientiarum Petropolitanae. Band 20, 1776, S. 189–207 (Online).
Gerd Fischer: Lineare Algebra: Eine Einführung für Studienanfänger. Springer, 2008, S. 307.
Michael Merz, Mario V. Wüthrich: Mathematik für Wirtschaftswissenschaftler. Vahlen, 2013, S. 244–245.

Weblinks

Wikiversity: Platon und Würfelsymmetrie – Kursmaterialien

Bernhard Elsner: Warum die Verknüpfung von Drehungen wieder eine ist. 8. September 2014, abgerufen am 18. April 2015 (geometrischer Beweis).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Leonhard Euler: Novi Commentarii academiae scientiarum Petropolitanae. Band 20, 1776, S. 189–207 (Online).

[fischer-2] Gerd Fischer: Lineare Algebra: Eine Einführung für Studienanfänger. Springer, 2008, S. 307.

[merz-3] Michael Merz, Mario V. Wüthrich: Mathematik für Wirtschaftswissenschaftler. Vahlen, 2013, S. 244–245.