Rollwiderstand

Der Rollwiderstand (auch: Rollreibung oder rollende Reibung) ist die Kraft, die beim Abrollen eines Rades oder Wälzkörpers entsteht und der Bewegung entgegengerichtet ist. Da der Rollwiderstand ungefähr proportional zur Normalkraft ist, wird als Kennwert der Rollwiderstandskoeffizient $c_{\mathrm {R} }$ (auch: Rollwiderstandsbeiwert. Rollreibungsbeiwert usw.) wie folgt gebildet:

F_{\mathrm {R} }=c_{\mathrm {R} }\cdot F_{\mathrm {N} }

- Der Rollwiderstand entspricht dem Rollwiderstandskoeffizient multipliziert mit der Normalkraft

Bei vergleichbaren Rahmenbedingungen ist die Rollreibung erheblich kleiner als die Gleitreibung. Bei vielen Anwendungen verursachen daher Wälzlager wie Kugellager geringere Verluste als Gleitlager. Bei höheren Geschwindigkeiten und Belastungen sind Gleitlager in der Regel nur konkurrenzfähig, wenn durch konstante Zufuhr eines Schmiermittels ein direkter Kontakt von Feststoffen durch einen dazwischen befindlichen Flüssigkeitsfilm verhindert werden kann.

Der Rollwiderstandskoeffizient $c_{\mathrm {R} }$ hängt neben der Materialpaarung auch von der Geometrie des Rollkörpers ab, insbesondere von seinem Radius.

Die Kraft, die überwunden werden muss, um einen runden Körper aus dem Stillstand in rotierende Bewegung zu versetzen, wird als Anfahrwiderstand bezeichnet. Bei Fahrzeugen ist der Rollwiderstand gemeinsam mit dem Losbrechwiderstand ein Teil des Fahrwiderstands.

Grundlagen

Asymmetrische Kontaktkraft

Kräfte während des Rollens

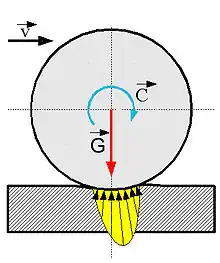
Beim Abrollen werden sowohl der rollende Körper (Wälzkörper) als auch die Unterlage (die Fahrbahn bzw. Wälzkörperbahn) verformt und zwar nahe dem Berührungspunkt bzw. der Berührungslinie. Im Wesentlichen handelt es sich dabei um eine elastische Verformung, es kommen jedoch Vorgänge hinzu, die einen Energieverlust verursachen. Insbesondere handelt es sich dabei um Walkarbeit im Reifengummi.

Insbesondere, wenn in das rollende Objekt Antriebs-, Verzögerungs- oder Führungskräfte eingeleitet werden, können auch Gleitreibungsanteile beim Abrollen auftreten. Bei Reifen also verstärkt bei Kurvenfahrt, beim Beschleunigen und Bremsen.

Auf nachgiebigem Untergrund spielt die Verdrängungsarbeit eine herausragende Rolle, die auf plastischer Verformung und innerer Reibung des Bodenmaterials beruht. So etwa beim Fahren auf feuchtem Erdboden, Schnee, Sand oder Splitt. Ähnliche Vorgänge können auch im Schotter des Gleisbettes auftreten.

Stahlrad läuft auf Schiene bei der Eisenbahn.

In nebenstehendem Bild wird durch das Rad die Schienenoberfläche elastisch verformt, bei Bewegung wird das Schienenmaterial in Fahrtrichtung gestaucht. Dabei türmt sich vor dem Rad ein Berg auf. Da sich das Schienenmaterial nur geringförmig bewegt, wird fortlaufend der Berg durch das Rad gewalzt und ebnet sich hinter dem Rad wieder ein. Beim Durchrutschen wird infolge des großen Flächendrucks das Material stark gepresst. Je häufiger eine Schiene befahren wird, desto eher können infolge der Pressung und Entspannung Teile der Oberfläche ausbrechen, was durch matte oder raue Oberflächen erkennbar wird. Ein Nebeneffekt ist die in einem nachgiebigen Schotterbett liegende Schienen-Schwellen Kombination, die dämpfend wirkt. Da sich das Rad während der Fahrt in dem „Tal“ der Eindruckstelle befindet, muss dieses auch bei horizontaler Strecke ständig neu gebildet werden. Es wandert während der Fahrt mit, was einen entsprechenden Energieverlust bedeutet. Der Effekt ist jedoch kleiner als der oben genannte. Hinzu kommt Reibung bei Kurvenfahrt aufgrund der starren Achsen.

Reifen auf nachgiebigem Untergrund

Wenn ein gummibereiftes Fahrzeug auf weichem Untergrund, wie lockerem Sand, fährt, wird das Fahren umso beschwerlicher, je schmaler die Reifen sind. Schmale Reifen sinken in weichem Untergrund ein. Der Reifen muss das Material verdrängen und zusätzlich die Reibung an den Reifenflanken überwinden. Geländegängige Fahrzeuge wie Mountainbikes besitzen daher breite Reifen. Reifen mit kleinem Durchmesser schieben eher einen Keil des Materials vor sich her, während Reifen mit größerem Durchmesser das aufgeworfene Material seitlich verdrängen bzw. zerteilen.

Gummireifen auf festem Fahrbahnbelag

Auf hartem Belag ist die Verformung des Gummireifens deutlich größer als die des Untergrunds. Eine feste Gummimischung sowie ein hoher Luftdruck des Reifens mindern Walkarbeit, Rollwiderstand und Berührungsfläche. Fahrräder für ausschließlich befestigte Untergründe werden mit schmalen Reifen und hohem Reifeninnendruck gefahren. Der hohe Druck sowie die geringe Wandstärke und Profilierung von schmalen Rennrad-Reifen haben jedoch einen größeren Einfluss auf den Rollwiderstand als die Reifenbreite und -größe an sich. Reifenbreite und -größe beeinflussen zwar indirekt über Gewicht, Luftwiderstand und Abrollverhalten bei Unebenheiten den Fahrwiderstand, den Rollwiderstand selber hingegen nur in geringem Maße.

Medizinbälle

Das Rollen eines schweren und nachgiebigen Medizinballs erfordert eine größere Anstrengung, da die weiche Füllung des Balles sich beim Rollen beständig plastisch verformt.

Rollwiderstandskoeffizient

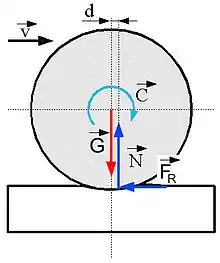
Durch die Verformung beim Abrollen verschiebt sich die Kontaktkraft zwischen Körper und Unterlage nach vorn (Abb. 1). Auf der zweiten Abbildung wurden die flächig wirkenden Kontaktkräfte durch die statisch äquivalente Normalkraft N ersetzt, die um die Strecke d gegenüber dem Aufstandspunkt verschoben ist, sowie durch die Reibungskraft F_R, die entgegen der Bewegungsrichtung wirkt.

Aus den Gleichgewichtsbedingungen ergibt sich für Räder bzw. Rollen mit Radius R bei konstanter Geschwindigkeit

F_{\mathrm {R} }={\frac {d}{R}}\cdot F_{\mathrm {N} }

Der Quotient ${\frac {d}{R}}$ ist der Rollwiderstandskoeffizient c_R (veraltet auch: Rollwiderstandsbeiwert oder Rollreibungsbeiwert):

c_{\mathrm {R} }={\frac {d}{R}}

Damit bekommt der Ausdruck für die Rollreibung F_R die Form

F_{\mathrm {R} }=c_{\mathrm {R} }\cdot F_{\mathrm {N} }

Mit
$R$ als Radius des Rades und
$F_{\mathrm {N} }$ als Normalkraft.

Wenn man den Rollwiderstand als Drehmoment versteht, ist $d$ der „Hebelarm“, an dem die Normalkraft angreift.

Der Rollwiderstandskoeffizient ist eine dimensionslose (einheitenfreie) Zahl, die von Materialeigenschaften und Geometrie des abrollenden Körpers abhängt (bei Reifen insbesondere auch vom Luftdruck). Typische Zahlenwerte des Rollwiderstandskoeffizienten liegen um ein bis über zwei Größenordnungen unter denen der niedrigsten Gleitreibungskoeffizienten.

Typische Rollwiderstandskoeffizienten c_R

c_R	Wälzkörper/Wälzkörperbahn
0,0005–0,001	Kugellager, Kugel und Lager aus gehärtetem Stahl⁴
0,001–0,002	Eisenbahnrad auf Schiene¹
0,015–0,02	Motorradreifen auf Asphalt
0,006–0,010	Autoreifen auf Asphalt, Lkw
0,011–0,015	Autoreifen auf Asphalt, Pkw
0,01–0,02	Autoreifen auf Beton²
0,02	Autoreifen auf Schotter
0,015–0,03	Autoreifen auf Kopfsteinpflaster²
0,03–0,06	Autoreifen auf Schlaglochstrecke²
0,045	Gleiskette (Kettenlaufwerk, Panzer Leopard 2) auf fester Fahrbahn
0,050	Autoreifen auf Erdweg
0,04–0,08	Autoreifen auf festgefahrenem Sand²
0,035–0,08	Gurtband (Raupenfahrwerk, Caterpillar Challenger und John Deere 8000T) auf Asphalt
0,2–0,4	Autoreifen auf losem Sand²^,³

¹ Gustav Niemann gibt für Eisenbahnräder folgende (aus Versuchen ermittelte) Formel an:

d=0{,}013\cdot {\sqrt {D}}

; d und D in mm. Bei 800 mm Raddurchmesser ergibt sich ca. 0,4 mm, was einem Koeffizienten von 0,001 entspricht.

² Quelle: Schmidt, Schlender 2003

³ Wer schon einmal versucht hat, am Strand Fahrrad zu fahren, kann diese hohen Zahlenwerte aus eigener Anschauung bestätigen

⁴ Quelle: Dubbel: Taschenbuch für den Maschinenbau

Grenzen der Theorie

Die oben beschriebene Beziehung $F_{\mathrm {R} }={\frac {d}{R}}\cdot F_{\mathrm {N} }=c_{\mathrm {R} }\cdot F_{\mathrm {N} }$ ist ein vereinfachtes Modell, welches für die meisten Berechnungen in der Technik ausreichend ist. Die Abhängigkeit der Rollreibung von weiteren Größen wie Kontaktkraft, Geschwindigkeit etc. wird hierbei nicht berücksichtigt (siehe auch Losbrechwiderstand).

Ferner betrachtet das beschriebene Modell nicht den möglichen Einfluss eines dritten Stoffes, der an der Grenzschicht zwischen Wälzkörper und Wälzkörperbahn vorhanden sein kann (Flüssigkeit oder Schmierstoff). Beispiele sind Schmierfett auf der Schiene oder Wasser auf der Straße. In einem solchen Fall wird von Mischreibung gesprochen.

Extreme Werte für Geschwindigkeiten und Temperaturen sowie eventuell chemische Einflüsse an den Kontaktstellen können mit diesem Modell nicht erfasst werden.

Literatur

Valentin L. Popov: Kontaktmechanik und Reibung. Ein Lehr- und Anwendungsbuch von der Nanotribologie bis zur numerischen Simulation. Springer-Verlag, 2009, ISBN 978-3-540-88836-9.

Weblinks

Schmidt, Schlender: Reifenwechsel unter technischen und klimatischen Aspekten. (Memento vom 29. September 2007 im Internet Archive) (PDF; 1,62 MB; 109 S.)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.