Risiko-Ertrags-Verhältnis

Das Risiko-Ertrags-Verhältnis ist in der Portfoliotheorie, einem Teilgebiet der Kapitalmarkttheorie, der Zielkonflikt, vor dem ein Kapitalmarktteilnehmer steht, wenn er Kapital als Kapitalanleger in ein Portfolio investiert.

Allgemeines

Der Zielkonflikt besteht für den Investor zwischen dem Risiko, das er bereit ist mit seiner Investition einzugehen, und dem Ertrag, den er erwartet. Generell ist steigender erwarteter Ertrag mit steigendem Risiko verbunden,[1][2] beide ökonomische Größen sind positiv miteinander korreliert.

Die wesentlichen Kennzahlen des Risiko-Ertrag-Verhältnisses sind zum einen RORAC und zum anderen RAROC.[3][4]

Historische Einordnung

In den 50er Jahren befasste sich Harry M. Markowitz als erster in der Geschichte mit dem Verhältnis zwischen Risiko und Ertrag. Es entstand das Portfolio-Selection Modell.

Auf diesen Erkenntnissen aufbauend, entwickelte unter anderem William F. Sharpe das Capital Asset Pricing Model. Diese Theorien nutzten viele Forscher, insbesondere Stephen Ross, um die Arbitragepreistheorie zu entwickeln.

Von den Erkenntnissen aus den Theorien profitieren Kapitalmarktteilnehmer (besonders Vermögensverwalter), indem sie über den Zielkonflikt zwischen Risiko und Ertrag nachdenken und diesen analysieren, bevor sie Entscheidungen treffen.[1]

Grundlagen

Ziel einer Investition

Der Ausgangspunkt für die Überlegungen zum Risiko-Ertrags-Verhältnis ist, dass ein Investor sein Kapital in ein Portfolio aus beispielsweise Aktien und/oder Anleihen anlegen möchte. Der Anleger ist an einer solchen Investition interessiert, weil er einen Anlageertrag erwirtschaften möchte, der über der Inflationsrate liegt. Es wird als Ziel des Anlegers postuliert, dass er den Konsum in die Zukunft zu verlagern und mit dem Anlageertrag zukünftig mehr Güter erwerben will als zum Zeitpunkt der Kapitalanlage.[2]

Charakteristika einer Anlage

Eine Anlage ist eine Investition, die dem Investor einen Geldstrom oder einen Leistungsstrom verspricht. Bei einem Leistungsstrom handelt es sich beispielsweise um Wohnungsleistungen an den Eigentümer eines Hauses. Dieser Leistungsstrom kann durch eine Vermietung des Hauses in einen Geldstrom umgewandelt werden.

Bei einem Geldstrom sind explizite und implizite Zahlungen möglich. Explizite Zahlungen sind beispielsweise Dividenden. Implizite Zahlungen dagegen sind zum Beispiel Kursänderungen. Bei letzterem handelt es sich um Kapitalgewinne oder Kapitalverluste, die bis zum Verkauf der Anlage nicht verwertet bleiben, sondern erst mit dem Verkauf realisiert werden.[2]

Es wird zwischen riskanten und risikolosen Anlagen (auch als risikofreie Anlagen bezeichnet) unterschieden, in die der Anleger sein Kapital investieren kann. Bei einer riskanten Anlage sind der Geld- und/oder der Leistungsstrom an den Anleger nicht sicher, sondern in der Regel zufällig und unsicher. Beispielsweise wissen Eigentümer von Aktien nicht, ob es eine Gewinnausschüttung geben wird und wenn ja, in welcher Höhe diese erfolgen wird. Bei einer risikolosen Anlage dagegen sind der Geldfluss und/oder der Leistungsstrom sicher. So können die Besitzer von kurzfristigen Schatzwechseln davon ausgehen, dass sowohl die Kupons, als auch der eingesetzte Betrag ausbezahlt werden, da es sich bei den Emittenten in diesem Fall um öffentliche Stellen handelt und der deutsche Staat aufgrund des Steuermonopols über ausreichend Kapital verfügt, um alle Schulden zu begleichen.[2][5]

Das magische Dreieck einer Vermögensanlage

Jede Anlage wird durch drei Charakteristika bestimmt: die Sicherheit, die Liquidität und die Rentabilität. Diese Kriterien sind nicht einzeln für sich zu betrachten, da sie sich gegenseitig beeinflussen.[6]

Die Sicherheit dient als Maßstab für den Erhalt des investierten Kapitals. Risiken, wie beispielsweise die Bonität des Kreditnehmers, aber auch Kursrisiken und Währungsrisiken bestimmen maßgeblich, ob eine Anlage sicher oder weniger sicher ist. Die Sicherheit kann durch die Streuung des einzusetzenden Kapitals erhöht werden. Diese Strategie wird als Risikodiversifizierung bezeichnet. Dabei kann das Risiko durch eine Verteilung des Vermögens auf verschiedene Wertpapierarten sowie durch eine Investition in unterschiedliche Länder und/oder Branchen minimiert werden.[6]

Die Liquidität gibt die Schnelligkeit an, mit der das eingesetzte Kapital in Bargeld oder Bankguthaben zurückgewandelt werden kann.[6] Die Liquidität einer Anlage steigt mit der Abnahme der Zeit, die zur Umwandlung benötigt wird.[7]

Die Rentabilität lässt sich aus dem Ertrag einer Anlage ableiten. Mögliche Erträge sind Dividenden, Zinsen, Kurssteigerungen und andere Ausschüttungen. Das Problem, das hier auftaucht, ist, dass ein Anleger in der Regel in beliebige Wertpapiere investieren wird, sodass sich die Ertragsarten erheblich unterscheiden können. Um die Rentabilität der unterschiedlichen Anlagen vergleichen zu können, wird die Kennzahl Rendite verwendet. Sie stellt das Verhältnis zwischen dem Ertrag und dem eingesetzten Kapital dar.[6]

Diese drei Kriterien bilden das magische Dreieck einer Vermögensanlage. Dieses Dreieck verdeutlicht, welche Konflikte bei einer Investition des Kapitals in ein Portfolio entstehen können:

Erstens entsteht ein Konflikt zwischen der Sicherheit und der Rentabilität. Je mehr Sicherheit von einem Anleger erwünscht wird, desto geringer wird die Rendite der Anlage sein. Je höher die Rentabilität sein soll, desto mehr Risiko muss eingegangen werden. Es ergibt sich folglich ein Zielkonflikt zwischen Risiko und Ertrag.

Zweitens besteht ein Konflikt zwischen der Liquidität und der Rentabilität. Anlagen, die über eine höhere Liquidität verfügen, weisen in der Regel Renditenachteile auf.[6]

Den Idealfall, der aus einer hohen Sicherheit, einer hohen Liquidität und einer hohen Rentabilität bestehen würde, gibt es aufgrund der Konkurrenz zwischen diesen Kriterien nicht.[7]

Zielkonflikt zwischen Risiko und Ertrag

Zusammenhang zwischen erwarteter Rendite, relativer Häufigkeit, Risiko und Standardabweichung

Ein Anleger erwartet einen bestimmten Ertrag, eine sogenannte Rendite, wenn er sein Kapital in ein Wertpapier investiert. Diese erwartete Rendite setzt man in vereinfachter Modellannahme oft dem Durchschnitt aller Renditen aus der Vergangenheit gleich, also dem empirischen Erwartungswert.[5]

Die tatsächliche Rendite der Anlage spiegelt den realisierten Ertrag aus der Investition wider und ist zum Zeitpunkt der Investition nicht bekannt.[2]

Das Risiko einer Investition besteht darin, dass die erwartete Rendite nicht erzielt wird und somit Abweichungen – nach oben oder unten – vom Erwartungswert entstehen. Die negative Abweichung stellt für den Investor gerade das Risiko dar.[5] Damit der Investor vor seiner Anlageentscheidung weiß, mit welchem erwarteten Ertrag und mit welchem Risiko er rechnen muss, werden die notwendigen Daten für diese Größen der Vergangenheit entnommen. Dabei lässt sich der Erwartungswert der Rendite bestimmen, indem die verschiedenen Ausprägungen der Renditen aus der Vergangenheit, gewichtet mit ihren relativen Häufigkeiten, zur Ermittlung von Erwartungswert und Standardabweichung verwertet werden. Die Abweichungen von der Rendite, mit denen in der Zukunft gerechnet wird, entsprechen somit den in der Vergangenheit beobachteten Abweichungen. Der finanzwirtschaftliche Begriff für Standardabweichung lautet Volatilität.[5][8] Mit steigender Volatilität steigt das Risiko, dass der tatsächliche Ertrag nicht dem erwarteten Ertrag entsprechen wird. Besitzt eine Investition überhaupt keine Volatilität (Wert Null), so handelt es sich um eine risikolose Anlage.[2][5]

Zur Vereinfachung wird im Folgenden die Wahl des Anlegers auf eine risikolose Investition (beispielsweise in kurzfristige Schatzwechsel) und eine risikoreiche Investition (beispielsweise in Aktien) begrenzt. Es handelt sich somit um ein Modell, bei dem eine Investition mit einer Standardabweichung von Null einer anderen Investition mit einer Standardabweichung größer Null gegenübergestellt wird. Dadurch wird gewährleistet, dass die Investitionen unabhängig sind. Thematisch befindet man sich innerhalb der Portfoliotheorie in einem effizienten Portfolio, das aus risikolosen und risikoreichen Wertpapieren besteht.[2][9] Die Zusammenhänge lassen sich entsprechend auf andere Anlageformen übertragen.[2]

Beispiel

Ein Anleger möchte 10.000 € investieren. Dabei hat er die Wahl zwischen kurzfristigen Schatzwechseln und Aktien.

Bei der risikolosen Anlage in die kurzfristigen Schatzwechsel werden dem Investor 4 % pro Jahr versprochen. Der erwartete Ertrag wird in diesem Fall dem tatsächlichen Ertrag entsprechen und der Kapitalmarktteilnehmer wird eine sichere Rendite von 4 % pro Jahr erhalten. Dies bedeutet, dass der Investor mit 400 € rechnen kann.
Die Aktien weisen dagegen schwankende Werte für das Merkmal „Rendite“ auf. Man spricht hier von verschiedenen Ausprägungen des Merkmals „Rendite“. Diese und die dazugehörenden relativen Häufigkeiten, mit denen die jeweiligen Ausprägungen in der Vergangenheit aufgetreten sind, können der folgenden Tabelle entnommen werden:

Ausprägungen des Merkmals „Rendite“	40%	20%	15%	−15 %	−20 %
relative Häufigkeit	6%	25%	38%	25%	6 %

Die erwartete Rendite der Aktien beträgt 8,15 %.

Der Anleger muss in diesem Fall entscheiden, ob er eine geringere Rendite mit einer größeren Sicherheit oder eine höhere Rendite, verbunden mit einer geringeren Sicherheit, bevorzugt. Eine Investition in die sicheren kurzfristigen Schatzwechsel wird dem Anleger sichere 4 % bringen. Für diese Anlage wird sich immer der Investor entscheiden, der Sicherheit präferiert. Ein Investor, der diese Risikoeinstellung aufweist, wird als risikoaverser Investor bezeichnet. Ist der Anleger bereit, ein größeres Risiko in Kauf zu nehmen, dann wird er sein Kapital in Aktien investieren und gleichzeitig als Ausgleich eine höhere Rendite verlangen. Die erwartete Rendite wird von 4 % auf 8,15 % steigen. Dabei kann der Investor bei einer Anlage in Aktien maximal 40 % gewinnen, einen Betrag von 4.000 €. Jedoch ist im schlimmsten Fall mit einem 20%igen Verlust zu rechnen. Dies entspricht 2.000 €. Für diese Investition wird sich in der Regel ein risikofreudiger Investor entscheiden.[1]

Jeder Anleger muss für sich selbst die Entscheidung treffen, wie viel er von seinem Kapital in die jeweilige Anlage investieren möchte. Grundsätzlich gibt es drei Möglichkeiten:

Das gesamte Kapital wird in kurzfristige Schatzwechsel investiert.
Das gesamte Kapital wird in Aktien investiert.
Das Kapital wird sowohl in Aktien als auch in kurzfristige Schatzwechsel investiert.[2]

Formale Herleitung des Zielkonflikts

Für eine formale Darstellung des Zielkonflikts zwischen Risiko und Ertrag werden folgende Größen benötigt: Der erwartete Ertrag aus der Anlage in risikolose Wertpapiere (hier kurzfristige Schatzwechsel) sei durch die Variable $\operatorname {E} _{f}\,$ dargestellt, der erwartete Ertrag aus der risikoreichen Anlage in Aktien durch die Variable $\operatorname {E} _{m}\,$ . Der tatsächlich eintretende Ertrag der riskanten Anlage wird mit $r_{m}\,$ bezeichnet. Der erwartete Ertrag der risikoreichen Anlage ist höher als der erwartete Ertrag der risikolosen Anlage, als Formel:

\operatorname {E} _{m}>\operatorname {E} _{f}\,

.

Wenn dieser Zusammenhang nicht gelten würde, dann würden die risikoaversen Anleger ausschließlich die risikolosen Wertpapiere kaufen, sodass die risikoreichen Wertpapiere unverkäuflich wären (hier geht die Annahme eines perfekt funktionierenden Marktes ein). Es gilt folgender mathematischer Zusammenhang:

\operatorname {E} _{p}=b\cdot \operatorname {E} _{m}+(1-b)\cdot \operatorname {E} _{f}\,

.

Der erwartete Ertrag aus allen Anlagen $\operatorname {E} _{p}\,$ entspricht dem gewichteten Durchschnitt der beiden erwarteten Erträge der Anlagen, wobei $b\,$ den Anteil angibt, der in die risikoreiche Anlage investiert wird. $(1-b)\,$ gibt somit an, welcher Anteil des gesamten investierten Kapitals in die risikolose Anlage fließt. Beispielsweise könnte die Hälfte des Kapitals zum Kauf von Aktien und die andere Hälfte zum Kauf von kurzfristigen Schatzwechseln genutzt werden. Unter der Annahme, dass die Aktien einen erwarteten Ertrag von 9 % und die kurzfristigen Schatzwechsel einen erwarteten Ertrag von 3 % aufweisen, wird der erwartete Ertrag der gesamten Investition 6 % betragen. Zur Beurteilung des Portfoliorisikos wird die Standardabweichung des Ertrags betrachtet, da diese den Maßstab für das Risiko bildet. Die Standardabweichung der Investition in risikoreiche Wertpapiere wird durch $\sigma _{m}\,$ repräsentiert. $\sigma _{p}\,$ repräsentiert die Standardabweichung des gesamten Portfolios.

Es gilt folgender mathematischer Zusammenhang:

\sigma _{p}=b\cdot \sigma _{m}\,

.

Die Standardabweichung des Portfolios entspricht dem Produkt aus dem Anteil, der in die risikoreiche Anlage investiert wird, und der dazugehörenden Standardabweichung. Nach Umformen und Einsetzen der beiden oberen Gleichungen ergibt sich der folgende Zusammenhang:

\operatorname {E} _{p}=\operatorname {E} _{f}+{\frac {(\operatorname {E} _{m}-\operatorname {E} _{f})}{\sigma _{m}}}\cdot \sigma _{p}

.

Bei dieser Gleichung handelt es sich um eine Budgetgerade, weil sie den Zielkonflikt zwischen dem erwarteten Ertrag ( $\operatorname {E} _{p}\,$ ) und dem Risiko ( $\sigma _{p}\,$ ) eines Portfolios darstellt. Die erhaltene Gerade kann in ein Diagramm eingezeichnet werden.

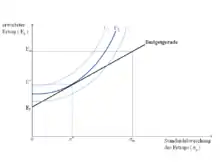
Der Zielkonflikt zwischen Risiko und Ertrag

${\frac {\operatorname {E} _{m}-\operatorname {E} _{f}}{\sigma _{m}}}\,$ stellt die Steigung der Funktion dar und $\operatorname {E} _{f}\,$ bildet den y-Achsenabschnitt. In der Grafik „Der Zielkonflikt zwischen Risiko und Ertrag“ ist diese Gerade schwarz eingezeichnet. Aus der Geradengleichung lässt sich ableiten, dass der erwartete Ertrag des Portfolios ( $\operatorname {E} _{p}\,$ ) steigt, wenn die Standardabweichung des Ertrags ( $\sigma _{p}\,$ ) steigt.

${\frac {\operatorname {E} _{m}-\operatorname {E} _{f}}{\sigma _{m}}}\,$ drückt den Preis des Risikos aus und beschreibt das zusätzliche Risiko, das ein Anleger in Kauf nehmen wird, um einen größeren erwarteten Ertrag zu erwirtschaften. Wenn der Investor kein Risiko mit seinem Kapital eingehen möchte, dann wird er sein gesamtes Kapital für kurzfristige Schatzwechsel ausgeben. Dies entspricht der ersten oben genannten Möglichkeit; hierbei ist $b=0$ und es wird lediglich der risikolose Ertrag ( $\operatorname {E} _{f}\,$ ) erzielt werden. Wünscht der Investor einen größeren erwarteten Ertrag, dann muss er mit einem größeren Risiko rechnen. Wenn er die zweite Möglichkeit wählt und sein gesamtes Kapital in Aktien anlegt, so ist $b=1$ , und der erwartete Ertrag des Portfolios entspricht dem erwarteten Ertrag aus der Investition in Aktien ( $\operatorname {E} _{m}\,$ ). Hierfür muss der Anleger allerdings ein hohes Risiko in Form der Standardabweichung $\sigma _{m}\,$ in Kauf nehmen. Der Investor kann aber auch die dritte Möglichkeit wählen und sowohl in Aktien, als auch in kurzfristige Schatzwechsel investieren. Dann würde der erwartete Ertrag des Portfolios zwischen dem risikolosen Ertrag ( $\operatorname {E} _{f}\,$ ) und dem risikoreichen Ertrag ( $\operatorname {E} _{m}\,$ ) und die Standardabweichung zwischen $0\,$ und $\sigma _{m}\,$ liegen.[2]

Lösung des Zielkonflikts

Zur Lösung des Zielkonflikts bedarf es der Bestimmung des optimalen Verhältnisses zwischen Risiko und Ertrag. Dazu muss bestimmt werden, wie viel der Investor in Aktien und wie viel er in kurzfristige Schatzwechsel investieren sollte, um den größtmöglichen Nutzen aus der Investition zu erzielen. Hierfür werden Indifferenzkurven in das Diagramm eingezeichnet. Jede Indifferenzkurve beschreibt einen bestimmten Nutzen, den der Kapitalmarktteilnehmer für unterschiedliche Kombinationen von Ertrag und Risiko erzielen kann bzw. wird. Dabei verläuft jede Kurve steigend, weil Risiko im Allgemeinen nicht erwünscht ist. Je größer das Risiko ist, desto höher muss der erwartete Ertrag als Ausgleich zum höheren eingegangenen Risiko sein.

Die Indifferenzkurve $U_{3}\,$ in der Grafik „Der Zielkonflikt zwischen Risiko und Ertrag“ stellt den größtmöglichen Nutzen dar, die Indifferenzkurve $U_{1}\,$ den geringsten Nutzen: Für ein gegebenes Risiko wird mit der Indifferenzkurve $U_{3}\,$ ein größerer erwarteter Ertrag erzielt als mit der Indifferenzkurve $U_{2}\,$ und mit der Indifferenzkurve $U_{2}\,$ ein größerer Wert als mit der Indifferenzkurve $U_{1}\,$ . Grundsätzlich würde ein Anleger diejenige Indifferenzkurve präferieren, die ihm den höchsten Nutzen stiftet. In diesem Fall wäre es die Indifferenzkurve $U_{3}\,$ . Jedoch ist diese Indifferenzkurve nicht erreichbar, weil diese Kurve die Budgetgerade nicht tangiert. Die Indifferenzkurve $U_{1}\,$ ist zwar erreichbar, es kann jedoch ein höherer Nutzen erzielt werden. Das optimale Verhältnis zwischen Risiko und Ertrag wird erst mit der Indifferenzkurve erreicht, die die Budgetgerade tangiert. In der Grafik „Der Zielkonflikt zwischen Risiko und Ertrag“ berührt die Indifferenzkurve $U_{2}\,$ die Budgetgerade.

Unterschiedliche Risikoeinstellungen

Folglich wird der Anleger sein Kapital auf die Aktien und die kurzfristigen Schatzwechsel so verteilen, dass ein erwarteter Ertrag in Höhe von $E^{*}\,$ bei einem Risiko von $\sigma ^{*}\,$ realisiert wird.[2]

Auswirkungen unterschiedlicher Risikoeinstellungen

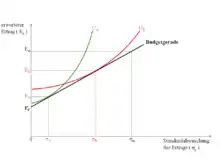
Aufgrund der unterschiedlichen Risikoeinstellungen der Investoren werden die Indifferenzkurven unterschiedliches Aussehen annehmen. Die Grafik „Unterschiedliche Risikoeinstellungen“ verdeutlicht diesen Zusammenhang.

Anleger A ist ein äußerst risikoaverser Investor. Seine (grüne) Indifferenzkurve berührt die Budgetgerade in einem Punkt mit einem niedrigen erwarteten Ertrag und einem niedrigen Risiko. Der Anleger wird sein Kapital hauptsächlich in kurzfristige Schatzwechsel anlegen und $\operatorname {E} _{A}\,$ als Ertrag erwarten, einen etwas größeren Wert als den risikolosen Ertrag ( $\operatorname {E} _{f}\,$ ). Da Anleger B ein risikofreudiger Investor ist, wird er sein Kapital größtenteils in Aktien anlegen, dabei viel mehr Risiko eingehen und dafür eine höhere Rendite erwarten. Seine (rote) Indifferenzkurve berührt die Budgetgerade deshalb bei einem höheren erwarteten Ertrag, nämlich $\operatorname {E} _{B}\,$ .[2]

Literatur

David E. Bell: Risk, Return, and Utility. MANAGEMENT SCIENCE/Vol. 41, No. 1, Januar 1995.
Richard A. Bettis, Vijay Mahajan: Risk/Return Performance of Diversified Firms. MANAGEMENT SCIENCE/Vol. 31, No. 7, Juli 1985.
Thomas Wolke: Risikomanagement. Oldenbourg Wissenschaftsverlag GmbH, München 2008, ISBN 978-3-486-58714-2.
Peter Albrecht, Raimond Maurer: Investment- und Risikomanagement. Schäffer-Poeschel Verlag Stuttgart, Stuttgart 2008, ISBN 978-3-7910-2827-9.
Neil Doherty: Integrated Risk Management: Techniques and Strategies for Managing Corporate Risk. McGraw-Hill, Inc., New York 2010, ISBN 978-0-13-800617-4.

Weblinks

Einzelnachweise

John C. Hull: Risk Management and Financial Institutions. Second Edition, Prentice Hall International, 2009, S. 1–2, ISBN 978-0138006174.
Robert S. Pindyck, Daniel L. Rubinfeld: Mikroökonomie. 6. Auflage, Pearson Studium, 2005, S. 216–218, S. 239–246, ISBN 978-3827371645.
Christian Fähnrich, Denise Manns: Konzeptionsentwicklung im Treasury-Management für Banken - Unter besonderer Berücksichtigung der Zinsbuchsteuerung. Diplomica Verlag GmbH, 2008, S. 12, ISBN 978-3-8366-5905-5.
Roland Eller (Autor), Walter Gruber (Autor), Markus Reif (Herausgeber): Risikomanagement und Risikocontrolling im modernen Treasury-Management. Deutscher Sparkassen Verlag, 2002, S. 51–53, ISBN 978-3093012907.
Martin Bösch: Finanzwirtschaft - Investition, Finanzierung, Finanzmärkte und Steuerung. Verlag Franz Vahlen München, 2009, S. 59–62, S. 224, ISBN 978-3-8006-3634-1.
HypoVereinsbank: Basisinformationen über Vermögensanlagen in Wertpapieren - Grundlagen, wirtschaftliche Zusammenhänge, Möglichkeiten und Risiken. Copyright 2008 by Bank-Verlag Medien GmbH, November 2008, S. 9–10, ISBN 978-3-86556-174-9.
Angela Steiner: Investmentfonds oder Lebensversicherung? - Altersarmut vermeiden durch die richtige Geldanlage. Diplomica Verlag GmbH, 2010, S. 32–33, ISBN 978-3-8366-8902-1.
Heinz Griesel, Helmut Postel, Friedrich Suhr unter Mitwirkung von Andreas Gundlach (Herausgeber): LK - Elemente der Mathematik - Leistungskurs Stochastik - mit Orientierungswissen - Lineare Algebra/Analytische Geometrie. Schroedel Verlag, 2007, S. 109, ISBN 3-507-83938-5.
Thomas Werner: Ökologische Investments - Chancen und Risiken grüner Geldanlagen. 1. Auflage, Gabler Verlag, 2009, S. 224–227, ISBN 978-3-8349-0741-7.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Hull-1] John C. Hull: Risk Management and Financial Institutions. Second Edition, Prentice Hall International, 2009, S. 1–2, ISBN 978-0138006174.

[Pindyck-2] Robert S. Pindyck, Daniel L. Rubinfeld: Mikroökonomie. 6. Auflage, Pearson Studium, 2005, S. 216–218, S. 239–246, ISBN 978-3827371645.

[Fähnrich-3] Christian Fähnrich, Denise Manns: Konzeptionsentwicklung im Treasury-Management für Banken - Unter besonderer Berücksichtigung der Zinsbuchsteuerung. Diplomica Verlag GmbH, 2008, S. 12, ISBN 978-3-8366-5905-5.

[Eller-4] Roland Eller (Autor), Walter Gruber (Autor), Markus Reif (Herausgeber): Risikomanagement und Risikocontrolling im modernen Treasury-Management. Deutscher Sparkassen Verlag, 2002, S. 51–53, ISBN 978-3093012907.

[Bösch-5] Martin Bösch: Finanzwirtschaft - Investition, Finanzierung, Finanzmärkte und Steuerung. Verlag Franz Vahlen München, 2009, S. 59–62, S. 224, ISBN 978-3-8006-3634-1.

[HypoVereinsbank-6] HypoVereinsbank: Basisinformationen über Vermögensanlagen in Wertpapieren - Grundlagen, wirtschaftliche Zusammenhänge, Möglichkeiten und Risiken. Copyright 2008 by Bank-Verlag Medien GmbH, November 2008, S. 9–10, ISBN 978-3-86556-174-9.

[Steiner-7] Angela Steiner: Investmentfonds oder Lebensversicherung? - Altersarmut vermeiden durch die richtige Geldanlage. Diplomica Verlag GmbH, 2010, S. 32–33, ISBN 978-3-8366-8902-1.

[Stochastik-8] Heinz Griesel, Helmut Postel, Friedrich Suhr unter Mitwirkung von Andreas Gundlach (Herausgeber): LK - Elemente der Mathematik - Leistungskurs Stochastik - mit Orientierungswissen - Lineare Algebra/Analytische Geometrie. Schroedel Verlag, 2007, S. 109, ISBN 3-507-83938-5.

[Werner-9] Thomas Werner: Ökologische Investments - Chancen und Risiken grüner Geldanlagen. 1. Auflage, Gabler Verlag, 2009, S. 224–227, ISBN 978-3-8349-0741-7.