Polariton

Ein Polariton ist in der Physik ein Quasiteilchen, das bei starker Wechselwirkung (Kopplung) eines elektromagnetischen Feldes mit einem angeregten Zustand entsteht (zum Beispiel einem Phonon oder Exziton in einem Festkörper, der ein Dipolmoment besitzt).

Ein typisches Beispiel ist die Kopplung einer kollektiven mechanischen Gitter-Schwingung (Phonon mit Frequenzen im optischen Bereich und transversaler Polarisation) eines Festkörpers an eine elektromagnetische Welle (Photon). Typischerweise bilden sie in ionischen Kristallen in Wechselwirkung mit Photonen Polaritonen. Exzitonen sind Teilchen-Loch-Anregungen in Halbleitern oder Isolatoren, die ebenfalls in Wechselwirkung mit Photonen Polaritonen bilden. In Metallen bilden Oberflächenplasmonen mit Photonen ebenfalls Polaritonen, was zu bedeutenden Anwendungen führte, da auf diese Weise Licht im Nanobereich manipuliert werden kann, weit unterhalb von dessen Beugungsgrenze. Fängt man Exzitonen in einer Falle (Quantentopf) und platziert sie in einem Mikroresonator für die angekoppelten Photonen, kann man ein kohärentes Bose-Einstein-Kondensat der Polaritonen erzeugen. Vereinfacht kann man sich Polaritonen als Licht vorstellen, dem im Festkörper sonst nur von massiven Teilchen bekannte Eigenschaften (Masse, abstoßende Wechselwirkung) zugeordnet werden. Zum Beispiel kann man sie einem konstanten Kraftfeld aussetzen in der sie eine einer Wurfparabel ähnliche Bewegung zeigen (Slow Reflection).[1]

Die Polaritonen sollten nicht mit den Polaronen verwechselt werden. Bei Letzteren hat man es mit fermionischen Quasiteilchen zu tun, z. B. mit einem Elektron plus „mitgeschleppter Polarisationswolke“, während die Polaritonen bosonische Quasiteilchen darstellen.

Geschichte

Die ersten theoretischen Überlegungen stammen von Kirill Borissowitsch Tolpygo, der 1950 einen gebundenen Zustand von optischen Phononen und Photonen vorhersagte.[2] Solomon Isaakowitsch Pekar nannte sie leichte Exzitonen, es setzte sich aber der von John Hopfield eingeführte Name Polariton durch. Unabhängig von Tolpygo führte Huang Kun 1951 Polaritonen ein.[3][4]

Der Fall von Plasmonen betrifft nicht Ionenkristalle oder Halbleiter, sondern zum Beispiel das Elektronengas in Metallen mit theoretischen und experimentellen Pionierarbeiten in den 1950er Jahren. Über Oberflächenplasmon-Polaritonen (Surface Plasmon Polariton, SPP) wurde erstmals 1968 von Andreas Otto berichtet.[5]

Polaritonen in einem Festkörper

In einem Festkörper entsteht ein Polariton bei der Wechselwirkung einer elementaren Anregung (z. B. Phonon, Exziton oder Plasmon) mit Photonen. Die zugrundeliegenden physikalischen Phänomene sind Absorption, Reflexion bzw. Dispersion elektromagnetischer Strahlung durch den Festkörper.

Im Fall starker Kopplung der Photonen im Festkörper an andere elementare Anregungen lässt sich der Effekt nicht mehr störungstheoretisch beschreiben. Photon und die elementare Anregung bilden stattdessen ein neues Quasiteilchen – das Polariton. Starke Kopplung findet man, falls sich die Dispersionskurven von Photon und Anregung schneiden, das heißt, falls Energie und Impuls der Wechselwirkungspartner praktisch übereinstimmen.

Bezüglich der beteiligten Quasiteilchen unterscheidet man im Detail zwischen Phonon-Polariton, Exziton-Polariton oder Plasmon-Polaritonen.

Das Phonon-Polariton

Das Phonon-Polariton lässt sich in Kristallen mit ionischer Bindung (z. B. NaCl) finden. Bildlich gesprochen ruft eine elektromagnetische Welle eine Polarisation

{\vec {P}}=\varepsilon _{0}\chi {\vec {E}}

und damit eine Gitterverzerrung hervor. Umgekehrt wird eine transversal-optische Gitterwelle von einer elektromagnetischen Gitterwelle begleitet. Hierbei spielen zwei verschiedene Arten der Polarisation eine wichtige Rolle:

Die Ionenpolarisation beruht auf der Verschiebung der Gitterionen eines Ionenkristalls im elektrischen Feld.
Die elektronische Polarisation kann als Verschiebung der Elektronenwolke bezüglich der Kerne aufgefasst werden.

Beide können durch das Oszillatormodell beschrieben werden. Betrachtet man also ein Ionenpaar, so erhält man für jedes einzelne Ion die Differentialgleichung des gedämpften harmonischen Oszillators, auf den eine äußere Störung, das elektrische Feld, wirkt. Für die Dielektrizitätskonstante ergibt sich mit Hilfe der Lyddane-Sachs-Teller-Relation folgende wichtige Beziehung:

\varepsilon (\omega )=\varepsilon _{\infty }+{\frac {\omega _{0}^{2}\cdot (\varepsilon _{\mathrm {st} }-\varepsilon _{\infty })}{\omega _{0}^{2}-\omega ^{2}-i\gamma \omega }}

Beschreibung der eingeführten Variablen:

$\omega _{0}$ : Resonanzfrequenz des schwingungsfähigen Systems, also des Ions
$\varepsilon _{\mathrm {st} }$ : Dielektrizitätskonstante des betrachteten Materials bei Frequenzen weit unterhalb der Resonanzfrequenz $\omega _{0}$ ( $\mathrm {st} {\widehat {=}}$ „static“)
$\varepsilon _{\infty }$ : Dielektrizitätskonstante des betrachteten Materials bei Frequenzen weit oberhalb der Resonanzfrequenz $\omega _{0}$
$\gamma$ : Dämpfungskonstante des harmonischen Oszillators

Unter der Annahme einer ebenen Welle, erhält man mit Hilfe der Maxwell-Gleichungen die allgemeine Dispersionsrelation elektromagnetischer Wellen im Medium (mit der Wellenzahl k):

\omega ^{2}={\frac {c^{2}k^{2}}{\varepsilon (\omega )}}

Setzt man in diese die hergeleitete Gleichung ein, so erhält man (mit $\gamma =0$ ) die Dispersionsrelation der Polaritonen:

\omega ^{2}\cdot \left(\varepsilon _{\infty }+{\frac {\omega _{0}^{2}\cdot (\varepsilon _{\mathrm {st} }-\varepsilon _{\infty })}{\omega _{0}^{2}-\omega ^{2}}}\right)=c^{2}k^{2}

Das Exziton-Polariton

Exziton-Polariton Dispersion mit longitudinal (upper polariton branch, UPB) und transversal (lower polariton branch, LPB) Aufspaltung, als auch die Dispersionsrelation für Licht in Vakuum. Notiz:

k

entspricht

q

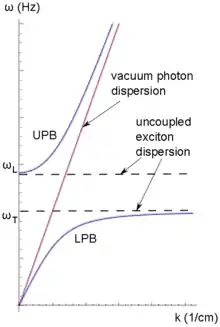
Das Exziton-Polariton entsteht wie das Phonon-Polariton aus der Wechselwirkung zwischen elektromagnetischen Wellen und Materie, z. B. bei Anregung bei der Photolumineszenz-Spektroskopie. Elektromagnetische Strahlung erzeugt im Festkörper eine Polarisation (siehe oben):

{\vec {P}}=\varepsilon _{0}\chi {\vec {E}}

Das heißt, dass die Materie teilweise polarisiert wird. Elektromagnetische Wellen sind im Vakuum transversal polarisiert. In Materie bildet sich allerdings auch eine longitudinale Polarisation aus.

Exzitonen senden bei der Rekombination elektromagnetische Strahlung aus. Diese Strahlung wechselwirkt mit dem Festkörper bzw. dessen Polarisation. Dabei "entsteht" das Exziton-Polariton. Elektromagnetische Wellen als auch Exzitonen besitzen eine Dispersion. Bei der Wechselwirkung dieser beiden Teilchen entsteht das Polariton, welches mit der Exziton-Polaritondispersion beschrieben wird (siehe Bild: Exziton-Polariton Dispersion).

Longitudinale und transversale Polarisation, bzw. entsprechend das longitudinale und transversale Polariton, spalten sich energetisch auf. Im Bild ist der Verlauf der ungekoppelten Exzitondispersion (gestrichelte Linien) gezeigt, allerdings schon in der longitudinalen und transversalen Aufspaltung, wie sie als Anteil zur Exziton-Polaritondispersion beiträgt. Die Dispersion von Photonen in Vakuum (ungekoppelt/ohne Wechselwirkung) ist rot gezeichnet.

Polariton-LT-Aufspaltung zwischen longitudinaler und transversaler Mode, gezeigt an fiktivem Messergebnis; grün: zwei Exziton-Peaks mit konstantem Untergrund, blau: sich ergebende Messkurve; auffällig ist die Verschiebung der Peakmaxima aufgrund der Überlagerung, was zeigt, dass bei genauen Ergebnissen immer gefittet werden sollte

Mit der Wechselwirkung knickt das longitudinale Exziton-Polariton ( $\omega _{L}$ ) vom Ursprung ausgehend ( $k=0$ ) ab und nähert sich asymptotisch der ungekoppelten Dispersion der Photonen an (UPB und dessen Verlauf in Blau). Beim transversalen Zweig knickt das Exziton-Polariton vom Verlauf der Photonen mit der Kopplung (Wechselwirkung) ab und nähert sich asymptotisch der Dispersion des transversalen Exzitons ( $\omega _{T}$ ) an (LPB und dessen Verlauf in Blau). Die Aufspaltung ist im Ursprung zwischen UPB und LPB als Differenz der gestrichelten Linien erkennbar, welche einer Energie entspricht, da

E=\hbar \cdot \omega

.

Im Experiment ist dieser Unterschied erkennbar. Exzitonen werden aus einem Elektron aus dem Leitungsband und einem Loch aus dem Valenzband gebildet, wobei es drei Valenzbänder gibt, welche energetisch absteigend A, B und C genannt werden. Diese sind z. B. im Schemabild der Photolumineszenz-Spektroskopie zu sehen. Alle Exzitonen spalten LT auf. Somit spaltet jedes Exziton auf. Messen kann man diese Aufspaltung der Exzitonen in Photolumineszenzspektroskopie mit sehr guter Auflösung. Dabei erscheinen alle strahlenden Ereignisse als Peaks, wie auch die exzitonischen Ereignisse. In der Messung sind dann jeweils zwei Peaks, statt einem, zu sehen, wobei der Abstand auf der Energieskala dann der Aufspaltung entspricht (siehe Bild: Polariton-LT-Aufspaltung).

Die Aufspaltung kann z. B. in Zinkoxid (ZnO) kaum messbar (ca. 0,2 meV: bei einem der A-Valenzband-Exziton-Polaritonen) oder messbar (ca. 10 meV: bei einem der B-Valenzband-Exziton-Polaritonen) sein.

Bose-Einstein-Kondensate von Polaritonen und Polariton-Laser

Atac Imamoglu schlug 1996 mit Kollegen als Erster vor, dass Polaritonen Bose-Einstein-Kondensate (BEC) bilden. Das ermöglichte das Konzept des Polariton-Lasers, eines Lasers ohne Inversion. Nachweise wurden durch H. Deng und Kollegen 2002[6] und durch Benoit Devaud und Kollegen erbracht.[7] Polariton-BEC in einer Falle (also unter kontrollierten Bedingungen) gelang 2007 David W. Snoke[8] und 2009 Jacqueline Bloch.[9] 2013 fand man Anzeichen für Suprafluidität in Polariton-BEC[10], was auch bei Raumtemperatur beobachtet wurde.[11] Typischerweise werden Exziton verwendet, die in Quantentöpfen gefangen sind und mit Licht in einem auf die Wellenlänge des Lichts abgestimmten Mikroresonator im Mikrometerbereich wechselwirken. Darin wird über die starke Korrelation im Bose-Einstein-Kondensats Kohärenz erzeugt, was sich auch auf das Licht überträgt (Laser).

Während bis dahin die Beobachtungen in Nichtgleichgewichtssystemen erfolgten wurden durch David W. Snoke, Keith Nelson und Mitarbeitern BEC im thermischen Gleichgewicht beobachtet.[12] Außerdem wurden die experimentellen Ergebnisse durch optisches Pumpen erbracht, Anregung durch elektrische Injektion wurde aber 2013 nachgewiesen, was technische Anwendungen in der Halbleitertechnik näher rückte.[13][14]

Literatur

Charles Kittel: Einführung in die Festkörperphysik. Oldenbourg Wissenschaftsverlag, 2005, ISBN 3-486-57723-9, S. 449 ff. (eingeschränkte Vorschau in der Google-Buchsuche).
Gerd Czycholl: Theoretische Festkörperphysik. Springer, 2007, ISBN 978-3-540-74789-5, S. 340 ff. (eingeschränkte Vorschau in der Google-Buchsuche).

Polariton-BEC:

David Snoke, Peter Littlewood: Polariton condensates Physics Today, Band 63, August 2010, S. 42
H. Deng, H. Haug, Y. Yamamoto: Exciton-polariton Bose-Einstein condensation, Reviews of Modern Physics, Band 82, 2010, S. 1489
T. Byrnes, Na Young Kim, Y. Yamamoto: Exciton–polariton condensates, Nature Physics, Band 10, 2014, S. 803
Benoit Devaud: Exciton-Polariton Bose-Einstein Condensates, Annual Review of Condensed Matter Physics, Band 6, 2015, S. 155–175
D. Sanvitto, S. Kéna-Cohen: The road towards polaritonic devices, Nature Materials, Band 15, 2016, S. 1061
D. W. Snoke, J. Keeling: The new era of polariton condensates, Physics Today, 70, 2017, Nr. 10, S. 54
Nick P. Proukakis, David W. Snoke, Peter B. Littlewood (Hrsg.): Universal themes of Bose-Einstein-condensation, Cambridge UP 2017

Weblinks

Video zur Erklärung eines Polaritons, University of Sheffield (youtube)
Being exceptional in higher dimensions, auf: nanowerk.com vom 1. Juli 2020: Magnon-Mikrowellen-Polaritonen

Einzelnachweise

Mark Steger, Chitra Gautham, David W. Snoke, Loren Pfeiffer, Ken West: Slow reflection and two-photon generation of microcavity exciton–polaritons, Optica, Band 2, 2015, Nr. 1, S. 1
Tolpygo, Zeitschrift für Experimentelle und Theoretische Physik, Band 20, Nr. 6, 1950, S. 497–509. Nachdruck in Englisch: : Physical properties of a rock salt lattice made up of deformable ions. In: Ukrainian Journal of Physics. 53, special edition, 2008, S. 497–509.
Kun, Lattice vibrations and optical waves in ionic crystals, Nature, Band 167, 1951, S. 779–780
Kun, On the interaction between the radiation field and ionic crystals, Proc. Roy. Soc. London, Band 208, 1951, S. 352–356
A. Otto, Excitation of nonradiative surface plasma waves in silver by the method of frustrated total reflection, Zeitschrift für Physik A, Band 216, 1968, S. 398–410
H. Deng u. a., Condensation of semiconductor microcavity exciton polaritons, Science, Band 298, 2002, S. 199
J. Kasprzak, B. Devaud u. a.: Bose-Einstein condensation of exciton polaritons, Nature, Band 443, 2006, S. 409
R. Balili, V. Hartwell, D.W. Snoke, L. Pfeiffer, K. West: Bose-Einstein Condensation of Microcavity Polaritons in a Trap, Science, Band 316, 2017, S. 1007–1010
E. Wertz, J. Bloch u. a.: Spontaneous formation of a polariton condensate in a planar GaAs microcavity, Applied Physics Letters, Band 95, 2009 S. 051108
A. Arno u. a., Superfluidity of polaritons in semiconductor microcavities, Nature Physics, Band 5, 2009, S. 805
Giovanni Lerario u. a., Room-temperature superfluidity in a polariton condensate, Nature Physics, Band 13, 2017, S. 837, Arxiv
Y.N. Sun u. a., Bose-Einstein Condensation of long-lifetime polaritons in thermal equilibrium, Physical Review Letters, Band 118, 2017, S. 016602
P. Bhattacharya, B. Xiao, A. Das, S. Bhowmick, J. Heo: Solid State Electrically Injected Exciton-Polariton Laser, Physical Review Letters, Band 110, 2013, S. 206403, PMID 25167434
Christian Schneider, Arash Rahimi-Iman, Na Young Kim, Julian Fischer, Ivan G. Savenko, Matthias Amthor, Matthias Lermer, Adriana Wolf, Lukas Worschech, Vladimir D. Kulakovskii, Ivan A. Shelykh, Martin Kamp, Stephan Reitzenstein, Alfred Forchel, Yoshihisa Yamamoto, Sven Höfling: An electrically pumped polariton laser, Nature, Band 497, 2013, S. 348–352, PMID 23676752

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Mark Steger, Chitra Gautham, David W. Snoke, Loren Pfeiffer, Ken West: Slow reflection and two-photon generation of microcavity exciton–polaritons, Optica, Band 2, 2015, Nr. 1, S. 1

[2] Tolpygo, Zeitschrift für Experimentelle und Theoretische Physik, Band 20, Nr. 6, 1950, S. 497–509. Nachdruck in Englisch: : Physical properties of a rock salt lattice made up of deformable ions. In: Ukrainian Journal of Physics. 53, special edition, 2008, S. 497–509.

[3] Kun, Lattice vibrations and optical waves in ionic crystals, Nature, Band 167, 1951, S. 779–780

[4] Kun, On the interaction between the radiation field and ionic crystals, Proc. Roy. Soc. London, Band 208, 1951, S. 352–356

[5] A. Otto, Excitation of nonradiative surface plasma waves in silver by the method of frustrated total reflection, Zeitschrift für Physik A, Band 216, 1968, S. 398–410

[6] H. Deng u. a., Condensation of semiconductor microcavity exciton polaritons, Science, Band 298, 2002, S. 199

[7] J. Kasprzak, B. Devaud u. a.: Bose-Einstein condensation of exciton polaritons, Nature, Band 443, 2006, S. 409

[8] R. Balili, V. Hartwell, D.W. Snoke, L. Pfeiffer, K. West: Bose-Einstein Condensation of Microcavity Polaritons in a Trap, Science, Band 316, 2017, S. 1007–1010

[9] E. Wertz, J. Bloch u. a.: Spontaneous formation of a polariton condensate in a planar GaAs microcavity, Applied Physics Letters, Band 95, 2009 S. 051108

[10] A. Arno u. a., Superfluidity of polaritons in semiconductor microcavities, Nature Physics, Band 5, 2009, S. 805

[11] Giovanni Lerario u. a., Room-temperature superfluidity in a polariton condensate, Nature Physics, Band 13, 2017, S. 837, Arxiv

[12] Y.N. Sun u. a., Bose-Einstein Condensation of long-lifetime polaritons in thermal equilibrium, Physical Review Letters, Band 118, 2017, S. 016602

[13] P. Bhattacharya, B. Xiao, A. Das, S. Bhowmick, J. Heo: Solid State Electrically Injected Exciton-Polariton Laser, Physical Review Letters, Band 110, 2013, S. 206403, PMID 25167434

[14] Christian Schneider, Arash Rahimi-Iman, Na Young Kim, Julian Fischer, Ivan G. Savenko, Matthias Amthor, Matthias Lermer, Adriana Wolf, Lukas Worschech, Vladimir D. Kulakovskii, Ivan A. Shelykh, Martin Kamp, Stephan Reitzenstein, Alfred Forchel, Yoshihisa Yamamoto, Sven Höfling: An electrically pumped polariton laser, Nature, Band 497, 2013, S. 348–352, PMID 23676752