Paradoxon der Längenkontraktion
Ein Paradoxon der Längenkontraktion entsteht, wenn die wechselseitige Längenkontraktion ohne Berücksichtigung der Relativität der Gleichzeitigkeit betrachtet wird. Diese Art von Paradoxon stellt das Gegenstück zum Zwillingsparadoxon dar, das aus der Zeitdilatation entspringt.
Gemäß der speziellen Relativitätstheorie ist ein Körper, der in einem Inertialsystem ruht, aus der Sicht von relativ dazu bewegten Inertialsystemen dem Effekt der Längenkontraktion unterworfen. Umgekehrt sind auch alle Körper, die im zweiten Inertialsystem ruhen, aus Sicht des ersten Inertialsystems kontrahiert. Dies führt zu unterschiedlichen Varianten dieses Paradoxons, wobei kinematische als auch dynamische Komponenten eine Rolle spielen. Durch Berücksichtigung der Relativität der Gleichzeitigkeit können die Probleme allesamt gelöst werden.
Garagenparadoxon


Eine Leiter und eine Garage bewegen sich aufeinander zu, wobei sich die Leiter aus Sicht der Garage in positiver x-Richtung bewegt.[1][2] Dabei soll vorausgesetzt werden, dass die Leiter im selben Bewegungszustand länger ist als die Garage, also die Ruhelänge der Leiter größer ist. Doch aus Sicht des Inertialsystems, in dem die Garage ruht, ist die Leiter in Bewegung, und aufgrund der Längenkontraktion kann die Leiter durch Wahl einer passenden Geschwindigkeit so klein gemacht werden, dass sie in die Garage passt (Fig. 1). Hingegen ist die Garage aus Sicht des Systems der Leiter bewegt und folglich kontrahiert. Aus dieser Perspektive ist die Garage kleiner und die Leiter kann unmöglich in die Garage passen (Fig. 2).
Auflösung
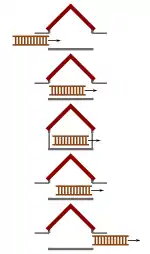
Dass solche Situationen nicht zu Widersprüchen führen, liegt an der Relativität der Gleichzeitigkeit, d. h. was ein Beobachter im Garagensystem als gleichzeitig wahrnimmt, ist nicht gleichzeitig für einen Beobachter im Leitersystem.
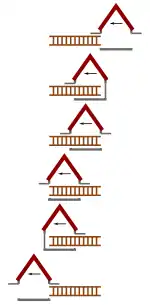
Dazu soll eine Garage mit zwei Toren (A = links, B = rechts, Fig. 3) betrachtet werden, die sich aus Sicht des Garagensystems – also gemessen mit in diesem System ruhenden Uhren – gleichzeitig öffnen, bevor die Leiter eingedrungen ist (Ereignisse A1 und B1), sich gleichzeitig schließen, wenn die Leiter vollständig eingeschlossen ist (A2 und B2), und sich unmittelbar darauf gleichzeitig wieder öffnen, um die Leiter durchzulassen (A3 und B3). Die Reihenfolge der Ereignisse ist also A1 = B1 vor A2 = B2 vor A3 = B3.
Hingegen gehen aus Sicht des Leitersystems (Fig. 4) aufgrund der Relativität der Gleichzeitigkeit die Uhren des Garagensystems von links nach rechts immer weiter vor, d. h. Ereignisse auf der rechten Seite finden vor Ereignissen auf der linken Seite statt. Zuerst öffnet sich also das rechte Tor (B1), und kurz bevor die Leiter in die Garage eindringen kann, auch das linke Tor (A1). Dann schließt sich das rechte Tor (B2) und öffnet sich unmittelbar darauf wieder (B3), wodurch das rechte Leiterende passieren kann. Inzwischen hat das linke Leiterende vollständig das linke Tor passiert. Dass auch dieses Tor sich unmittelbar darauf wieder schließt (A2) und öffnet (A3), hat keine Bedeutung mehr. Auf diese Weise kommt die Leiter in beiden Inertialsystemen unbeschadet durch die Garage. Die Reihenfolge der Ereignisse ist also B1 vor A1 vor B2 vor B3 vor A2 vor A3.
Im Zusammenhang mit dem ursprünglichen Paradoxon (mit geschlossener Hinterwand) sollen nun zwei Varianten diskutiert werden:
(1a) Die Leiter soll aus Sicht des Garagensystems augenblicklich in der Garage zum Stillstand kommen. Dies ist nur möglich, wenn jeder Teil der Leiter aus Sicht der Garage gleichzeitig beschleunigt wird. Ist sie auf diese Weise zur Ruhe gekommen, nimmt sie auch im Garagensystem wieder ihre Ruhelänge an, und da diese größer ist als die der Garage, wird sie während des Ausdehnungsprozesses an beide Innenwände der Garage gleichzeitig stoßen.
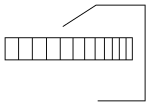
(1b) Im Leitersystem entsteht nun ein Problem aus der Tatsache, dass die Leiter länger ist als die Garage. Wie ist es möglich, dass das linke Leiterende auf die Innenseite des linken Garagenendes stoßen kann? Die Auflösung besteht darin, dass in beiden Systemen keine gleichzeitige Beschleunigung der beiden Leiterenden bzw. der beiden Garagenseiten erfolgen wird, die Übertragung der Beschleunigung von einem Ende des Objektes zum anderen Ende kann maximal mit v=c erfolgen. Im System der Garage wird zuerst der rechte Teil der Leiter beschleunigt und nimmt eine Geschwindigkeit an, die sich immer weiter derjenigen der Garage annähert. Das andere Ende der Leiter wird erst später abgebremst. Das führt automatisch dazu, dass diese Abschnitte der Leiter kontrahieren, bis schließlich die ganze Leiter erfasst ist. Aus Sicht des Leitersystems erfolgt eine Beschleunigung der Garage und zwar zuerst der Rückwand. Auch hier wird die Eingangstüre erst zu einem späteren Zeitpunkt erfasst. Dadurch ist es möglich, dass auch hier das linke Ende der Leiter vollständig in der Garage verschwindet, und die Leiter somit auf beiden Seiten an die Innenwände der Garage, allerdings nicht gleichzeitig, stoßen kann.
(2a) Im Gegensatz zur vorhergehenden Variante soll die Leiter nun nicht entlang ihrer gesamten Länge gleichzeitig im Garagensystem zum Stillstand kommen, sondern der Stillstand wird durch den Aufprall auf die Hinterwand verursacht. Aus Sicht der Garage kommt zuerst das rechte Ende der Leiter zum Stehen und expandiert folglich, da es nun seine Ruhelänge annimmt. Dies setzt sich fort bis zum anderen Ende der Leiter, sodass nach und nach die ganze Leiter ihre Ruhelänge annimmt und folglich während des Expansionsprozesses auch auf die andere Innenseite der Garage stößt.
(2b) Im Leitersystem entsteht abermals das Problem, wie es möglich sein soll, dass das linke Leiterende auf die Innenseite des linken Garagenendes stoßen kann. Die Antwort auf diese Frage ergibt sich aus der Tatsache, dass gemäß Relativitätstheorie keine starren Körper existieren können. Da die Beschleunigung in diesem Fall nur von einer Stelle ausgeht, und sich die Kopplungskräfte in der Leiter nicht schneller als mit Lichtgeschwindigkeit ausbreiten können, benötigt es Zeit, bis die Information des Zusammenstoßes das andere Ende der Leiter erreicht. Wie bei (1b) wird der rechte Teil der Leiter zuerst beschleunigt und nimmt eine Geschwindigkeit an, die sich immer weiter derjenigen der Garage annähert. D.h. aus Sicht des Leitersystems wird die Leiter wie eine Ziehharmonika aufgrund der Kollision zusammengestaucht, und das vorerst ruhende, linke Leiterende setzt sich erst dann in Bewegung, wenn die Leiter bereits vollständig im Innern der Garage eingeschlossen ist. Während des nun einsetzenden Expansionsprozesses (da im selben Bewegungszustand die Leiter länger ist als die Garage), wird auch hier das linke Ende der Leiter auf die linke Innenseite der Garage stoßen.
Panzerparadoxon
Dieses Paradoxon wurde erstmals von dem Physiker Wolfgang Rindler[3] eingeführt, wobei diverse Spielarten dieses Paradoxons auch als „Panzerparadoxon“[4] oder „Skifahrerparadoxon“[2] bekannt sind.
Es sei ein Graben mit einer „Ruhelänge“ von 10 m gegeben (also gemessen in seinem Ruhesystem bzw. dem Inertialsystem, in dem der Graben unbewegt ist), und ein relativ dazu bewegter Stab mit derselben Ruhelänge. Ist nun die Relativbewegung zwischen ihnen so hoch, dass ein Kontraktionsfaktor von 10 erreicht wird, dann bedeutet dies, dass aus Sicht des Grabens der Stab auf 1 m kontrahiert ist, während der Graben unverkürzt bleibt. Hingegen ist aus Sicht des Stabes der Graben auf 1 m kontrahiert, und der Stab ist unverkürzt. Dies führt zu der folgenden, scheinbar widersprüchlichen Situation.[3]
Gesetzt den Fall, dass der Graben mit einer Falltüre verschlossen ist, welche geöffnet wird, wenn der Stab sich gerade über dem Graben befindet, so müsste der auf 1 m kontrahierte Stab sofort, d. h. gleichzeitig entlang seiner ganzen Länge in den 10 m breiten Graben fallen. (Damit das tatsächlich passiert, sollte im Graben allerdings ein Elektromagnet vorhanden sein, der den Stab anzieht – denn die Gravitation kann im Rahmen der speziellen Relativitätstheorie nicht behandelt werden.) Für einen mit dem Stab mitbewegten Beobachter ist der Graben jedoch auf 1 m kontrahiert, und es gibt für diesen Beobachter (vorerst) keinen Grund anzunehmen, dass der 10 m lange „starre“ Stab in den nur 1 m breiten Graben fallen wird.
Auflösung
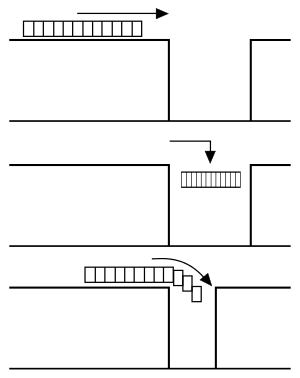
Die Auflösung dieses Paradoxons liegt nun darin, dass die Annahme des relativ zum Stab ruhenden Beobachters, nämlich dass der Stab „starr“ sei, falsch ist. D. h., es gibt keine „starren Körper“ in der speziellen Relativitätstheorie, da sich Wirkungen im Körper maximal mit Lichtgeschwindigkeit ausbreiten können, während der starre Körper der vor-relativistischen Physik auf der Annahme beruht, dass Wirkungen sich in ihm unendlich schnell ausbreiten. Außerdem muss die Relativität der Gleichzeitigkeit berücksichtigt werden. Die durch die spezielle Relativitätstheorie korrigierte Sicht des beim Stab ruhenden Beobachters lautet also: Die Falltür öffnet sich nicht an allen Punkten gleichzeitig. Und da die Kopplungskräfte im Stab aufgrund ihrer endlichen Ausbreitungsgeschwindigkeit (maximal Lichtgeschwindigkeit) Zeit für ihre Wirkung benötigen, kann der Stab seine „Starrheit“ nicht aufrechterhalten (d. h., die Kopplungskräfte im Stab reagieren zu langsam) und wird an den geöffneten Stellen der Falltür sofort beginnen, aufgrund der Wirkung des Magneten in den Graben zu „fließen“. Für den Fall, dass keine Falltür vorhanden ist, würde der Stab natürlich sofort beginnen zu zerfließen, wenn sich das erste Stabende über dem Graben befindet.
Sobald das vordere Ende des Stabes in die Grabenwand einschlägt, sind nach und nach, von vorne nach hinten, Teile des Stabes nun ruhend im Ruhesystem des Grabens, bis der ganze Stab in Vorwärtsrichtung still steht. Es gibt dann kein Ruhesystem des Stabes mehr, in welchem der Graben kürzer ist als der Stab, und somit kann der ganze Stab in jedem Fall in den Graben fallen.
Dagegen könnte eingewendet werden, dass zwar nun bewiesen sei, dass der Stab in beiden Inertialsystemen in den Graben fällt, jedoch würde er (wenn der Fallwinkel in beiden Systemen derselbe wäre) aus Sicht des Ruhesystems des Grabens deutlich tiefer an der gegenüberliegenden Wand einschlagen, da der zurückzulegende Weg und somit die Flugzeit hier deutlich länger sind, wogegen aus Sicht des Stabs der Graben und somit der zurückzulegende Weg deutlich kürzer ist, und somit der Aufschlagpunkt deutlich höher. Diese Einschätzung ist jedoch falsch: Denn die Beschleunigung und somit der Fallwinkel wird im System des Stabes deutlich ausgeprägter ausfallen (bzw. der relativistischen Aberration unterworfen sein), und somit trotz der kürzeren Distanz derselbe Punkt der Gegenwand getroffen, wie im Grabensystem.[2] Denn es muss berücksichtigt werden, dass das elektrische Coulomb-Feld im Graben aus Sicht des Stabes ebenso der Kontraktion unterworfen ist, wie der Graben selbst. Dies führt dazu, dass die Feldlinien des Coulomb-Feldes normal zur Bewegungsrichtung im Ruhesystem des Stabes deutlich dichter aneinandergedrängt sind, als im Ruhesystem des Grabens.[4]
In anderen Varianten wird auch das Szenario einer Schlacht zwischen zwei Armeen benutzt. Die eine Armee hebt nun einen Graben aus, von dem sie meint, dass er breit genug sei, damit der heranrasende feindliche Panzer hineinfällt. Um ganz sicher zu sein, wird dafür ein starker Elektromagnet benutzt. Hingegen glaubt die andere Armee, dass ihr Panzer mit Leichtigkeit über den aus ihrer Sicht kontrahierten Graben gelange. Das Weitere entspricht dem obigen Schema: Der Panzer wird sofort an den Punkten zu zerfließen beginnen, wo er frei über dem Graben schwebt (d. h. mit Falltür an den Orten, wo sich die Falltür zuerst öffnet, und ohne Falltür sofort nach Erreichen der Kante).[4]
Eine andere Variante beinhaltet einen Skifahrer während einer Abfahrt. Dieser kommt zu einer Gletscherspalte – aus Sicht des Gletschersystems müssten die kontrahierten Skier hineinfallen, hingegen sollten aus Sicht des Skifahrers die Skier problemlos über die kontrahierte Spalte kommen. Die Auflösung ist die gleiche wie oben: Die Skier zerfließen und schlagen an die Spaltwand.[2]
Maßstabsparadoxon
Ein Stab der Länge L bewege sich mit einer Geschwindigkeit v parallel zu einem ruhenden Loch, das ebenfalls die Länge L besitzt. Gleichzeitig bewegt sich der Stab noch mit einer kleinen, senkrechten Geschwindigkeit auf das Loch zu:[5][6]
(Für die beiden einleitenden Abbildungen werde v so klein gegen die Lichtgeschwindigkeit c angenommen, dass keine relativistischen Effekte hervortreten.)
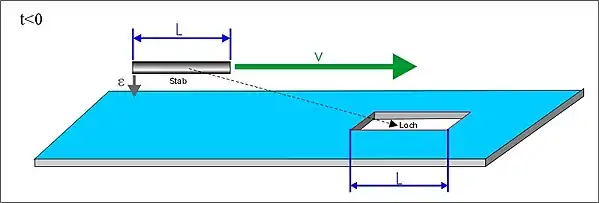
Zu einem geeigneten Zeitpunkt t = 0 durchquert der Stab parallel das ruhende Loch:
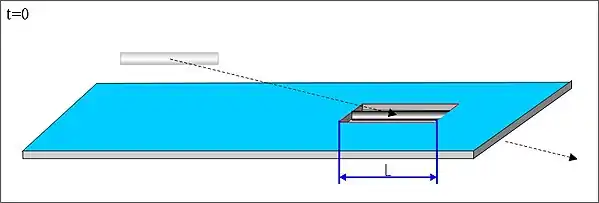
- Fall (A): Der Stab bewegt sich parallel auf das ruhende Loch zu.
Vom Bezugssystem des ruhenden Lochs aus betrachtet erscheint der schnell (hier mit ca. v = 0,94 c) bewegte Stab durch die Längenkontraktion verkürzt auf die Länge L’ < L und passt damit bequem durch das Loch:
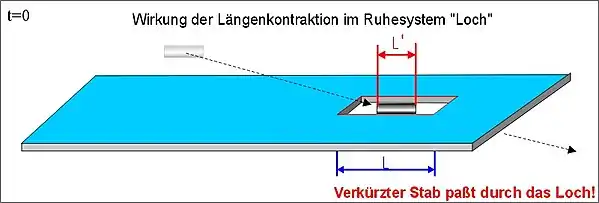
- Fall (B): Das Loch bewegt sich auf den ruhenden Stab zu
Betrachtet man die Situation allerdings vom mitbewegten System des Stabes aus, so ruht der Stab und das Loch bewegt sich relativ zum Stab mit der hohen Geschwindigkeit v auf den Stab zu: (In der oberen Abbildung bei t < 0 wird das Loch noch in der Länge L gezeigt, die es in Ruhe hat, bevor es auf v beschleunigt wird.)
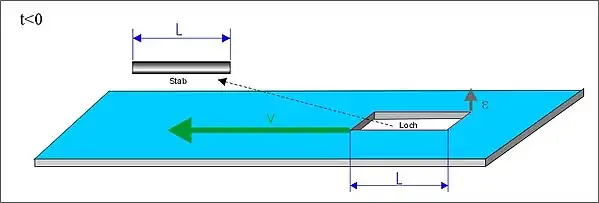
Vom Stab aus betrachtet, der in seinem Ruhesystem die Länge L besitzt, wirkt sich die Längenkontraktion jetzt auf das bewegte Loch aus, das nur noch die Länge L’ < L besitzt, sodass der Stab nicht mehr quer durch das Loch passt:
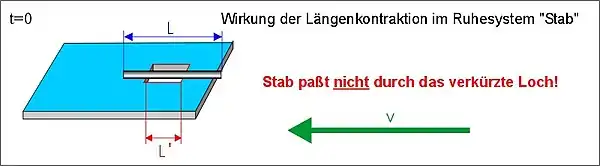
Das ist aber ein Widerspruch. Die Abmessungen können zwar wechselseitig verkürzt zueinander erscheinen; die Aussage aber, dass der Stab das Loch passiert, kann nicht von der Wahl des Bezugssystems abhängig gemacht werden; sonst wäre die Relativitätstheorie widersprüchlich und falsch.
Auflösung
Die Beschreibung Fall (A) (Der Stab bewegt sich parallel auf das ruhende Loch zu) entspricht der Realität und ist richtig dargestellt. Die Beschreibung Fall (B) (Das Loch bewegt sich auf den ruhenden Stab zu) wurde in der vorangestellten Darstellung nicht vollständig richtig nach den Gesetzen der Lorentz-Transformation durchgeführt und erzeugt damit das scheinbare Paradoxon, das tatsächlich gar nicht existiert. Bei der Transformation zum System im Fall (B) muss noch berücksichtigt werden, dass sich nicht nur die Ortskoordinaten entsprechend der Lorentz-Transformation ändern und so direkt zur Längenkontraktion führen, sondern dass auch die Zeit transformiert werden muss. Dadurch ändert sich aber auch die Sicht darauf, welche Ereignisse als gleichzeitig erscheinen. Im Fall (A) (ruhendes Loch) durchquert der Stab das Loch parallel, was bedeutet, dass sich das vordere und das hintere Ende des Stabes gleichzeitig zum Zeitpunkt t = 0 durch das Loch bewegen. Dabei durchquere das hintere Ende des Stabes das Loch am Ort x = 0, das vordere Ende des Stabes am Ort . Im Fall (B) bleibt diese Durchtritts-Gleichzeitigkeit an den beiden aktuellen Lochrand-Orten aber nicht erhalten, sondern die Zeit t’ im Stab-Ruhesystem berechnet sich nach der Lorentz-Transformation:
Wenn nun das hintere Ende des Stabes zum Zeitpunkt t = 0 und am Ort x = 0 das Loch durchquert, so geschieht das zu folgender Zeit im Stab-Ruhesystem:
Für das vordere Ende des Stabes (zum Zeitpunkt t=0, am Ort im Loch) geschieht das zu folgender Zeit im Stab-Ruhesystem:
Das vordere Ende des Stabes hat also das Loch viel früher durchstoßen als das hintere Ende des Stabes (betrachtet im System, das sich mit dem Stab mitbewegt). Dass das vordere Ende des „ruhenden“ Stabes das heranfliegende Loch zuerst durchquert, bedeutet anschaulich, dass das Loch nicht mehr parallel zum Stab fliegt, sondern verkippt erscheint, so dass sich korrekterweise das folgende transformierte Bild für den Fall (B) (Das Loch bewegt sich auf den ruhenden Stab zu) ergibt:

Stab und Loch fliegen in diesem System nicht mehr parallel aufeinander zu. Daraus folgt erstens: Gleichzeitige Ereignisse in einem Inertialsystem laufen in einem relativ dazu bewegten Inertialsystem nicht ebenfalls gleichzeitig ab, und zweitens sind „parallele“ Geraden im anderen Inertialsystem nicht mehr parallel: Der Winkel zwischen zwei Raumrichtungen wird von zwei sich relativ zueinander bewegenden Beobachtern unterschiedlich gemessen.
Die Argumentation kann auch andersherum durchgeführt werden: Geht man von einem ruhenden Stab aus, auf den sich tatsächlich ein Loch parallel zubewegt, dann erzeugt die Transformation in das System des ruhenden Lochs (Fall (A)) nun die Verkippung des Stabes (in der vorherigen Darstellung war es genau umgekehrt, dort wurde das Loch verkippt und nicht der Stab). Das Maßstabsparadoxon lässt sich so in jedem Fall widerspruchsfrei im Rahmen der Relativitätstheorie auflösen.
Literatur
- Wolfgang Rindler: Essential relativity. Birkhäuser, Boston 1977, ISBN 3-540-07970-X, S. 41–42.
- Eckhard Rebhan: Theoretische Physik I. Spektrum, Heidelberg/Berlin 1999, ISBN 3-8274-0246-8, S. 791–793.
- Rindler, Wolfgang: Length Contraction Paradox. In: Am. J. Phys.. 29, Nr. 6, 1961, S. 365–366. doi:10.1119/1.1937789.
- Roman Sexl, Herbert K. Schmidt: Raum-Zeit-Relativität. Vieweg, Braunschweig 1979, ISBN 3-528-17236-3.
- Ulrich E. Schröder: Spezielle Relativitätstheorie. Verlag Harri Deutsch, 2005, ISBN 3-8171-1724-8.
- Richard Lenk: Brockhaus-abc-PHYSIK, Band 2, 2. Auflage, F.A. Brockhaus Verlag, Leipzig 1989, ISBN 3-325-00192-0.
Weblinks
- Physik-FAQ: Längenparadoxon
- Physics FAQ: The Barn and the Pole